基于多带宽局部多项式的时空地理加权分位数回归分析

1 引言

回归分析作为常用的空间统计方法，可以对空间关系进行建模、检查和探究。早期空间统计分析方法多从全局的角度假设空间变量关系是固定的，忽略了现实地理世界空间关系的异质性，因而并不能反映回归参数的真实空间特征。1996年，Brunsdon等在总结前人关于局部回归和变参数研究的基础上，提出了基于空间变化关系建模的局部线性回归方法——地理加权回归模型(Geographically Weighted Regression，GWR)。地理加权回归通过建立空间范围内每个点处的局部回归方程，来探索研究对象在某一尺度下的空间变化及相关驱动因素，很好地解释了变量的局部空间关系与空间异质性，因而在相关领域得到了广泛应用。

空间位置是影响城市住宅价格的关键因素，近年来地理加权回归分析在住宅价格影响因子建模分析方面受到了广泛关注。地理加权回归模型虽然考虑了事物的空间变化，却未考虑时间变化。而现实世界中变量间的关系或者结构往往还会随着时间而改变，例如市场趋势、通货膨胀等驱动因子的时间效应对于住宅价格的影响也不可忽略。为了考虑时间动态性，Huang等在地理加权回归模型中加入了时间因素，把时间和空间信息整合到权矩阵中，并提出了在建立的椭球坐标系中以观测位置的时空距离函数为权值的估计方法，称之为时空地理加权回归方法(Geographically and Temporally Weighted Regression)简称GTWR。近年来，GTWR一直被不断地创新和演化，时空地理加权自回归模型和基于局部多项式求解的GTWR等分析方法相继被提出。

图1 研究基本框架

2 研究方法

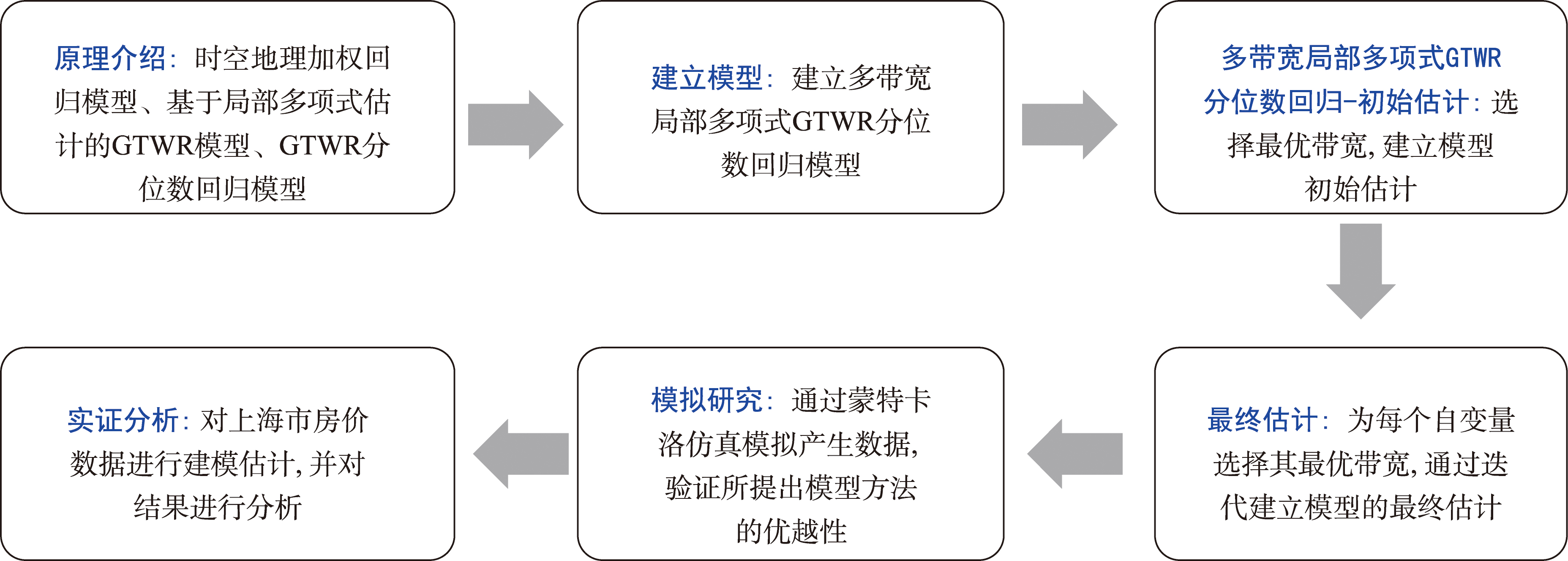
本研究的基本框架如图1所示，包含建立模型及模型估计、蒙特卡洛仿真模拟及实际数据分析等部分。

2.1 时空地理加权回归模型

时空地理加权回归模型具有如下形式：

Y_i = β₀(u_i,v_i,t_i) + ∑_j=1^pβ_j(u_i,v_i,t_i)X_ij + ε_i (i=1,2,⋯,n)

2.2 基于局部多项式估计的GTWR模型

时空地理加权回归模型(1)的上述估计方法本质上属于NW核估计方法，该方法存在边界效应，因此在这里考虑局部多项式估计。假设式(1)中的每个系数函数β_j(u,v,t)(j=1,2,⋯,p)关于空间位置坐标u,v和时间坐标t均有连续的q+1阶偏导数。

2.3 多带宽局部多项式GTWR分位数回归模型

假定误差项ε_i{i=1,...,n}为独立同分布的序列，且分布情况未知，则Y的τ条件分位数为m_τ(x)=argmin_θ∈RE{ρ_τ(Y-θ∣X=x)。其中，ρ_τ(x)=x[τI(x≥0)-(1-τ)I(x<0)]为分位数回归领域的分位数损失函数，有些地方也称之为对号函数(check function)。I(∙)为示性函数。

表1 GWR及其变种以及本文方法的原理、公式、适用条件及参考文献
分类	原理	公式编号	适用条件
地理加权回归（GWR）	基于局部最优思想(局部常数估计）的空间变系数回归模型	(15)	针对存在空间非平稳性的空间数据
混合地理加权回归(Mixed-GWR)	在GWR模型基础上，结合OLS回归模型，同时考虑数据的局部和全局变化情况，将模型参数分为全局和局部两种尺度特征，利用后向迭代算法对模型进行估计	(16)	针对同时存在全局平稳性和局部非平稳性的空间数据
时空地理加权回归（GTWR）	GWR模型基础上增加时间维度	(17)	针对存在时空非平稳性的时空数据
基于多带宽局部多项式的时空地理加权分位数回归模型(本文方法)	分位数回归、局部多项式估计、多尺度多带宽与时空地理加权回归方法相结合	(24)	针对不满足高斯-马尔可夫假设的时空数据，如存在异常值、异方差、或厚尾分布。针对多元时空数据关系对应不同解释变量的变化尺度的情况，解决时间、空间尺度效应问题。研究解释变量对响应变量分布的影响，研究解释变量对响应变量多个分位数的影响

3 模拟研究

本节采用蒙特卡洛仿真实验来探索本文方法的有限样本表现，通过比较本文的基于多带宽局部多项式的时空地理加权分位数回归模型(Q)和多带宽时空地理加权最小二乘回归模型(LS)在不同仿真实验设定下的表现来展现本文方法的优越性。

表2 通过2种方法得到的系数函数估计的MSE和MAE的均值和标准差(n=1000,m=200)
τ	β_p	MSE_Q	MSE_LS	MAE_{QMAE_LS}
τ=0.5	β₀	0.0468(0.0225)	0.0530(0.0260)	0.1761(0.0441)	0.1851(0.0468)
	β₁	0.0062(0.0036)	0.0094(0.0065)	0.0636(0.0195)	0.0761(0.0266)
	β₂	0.1112(0.0499)	0.1216(0.0613)	0.2569(0.0623)	0.2710(0.0645)
	β₃	0.0059(0.0020)	0.0078(0.0028)	0.0605(0.0120)	0.0697(0.0129)

表2表明在0.5分位数(τ=0.5)，0.75分位数(τ=0.75)和0.25分位数(τ=0.25)下，所有系数的分位数回归估计量的AMSE和AMAE均比最小二乘估计量小，且MSE和MAE的标准差也较小。当分位数(τ=0.75)时，分位数回归与最小二乘回归结果差距较大，尤其是系数β₀和β₂的表现，基于最小二乘回归系数估计的AMSE是基于分位数回归系数估计的10倍，而基于最小二乘回归系数估计的AMAE是基于分位数回归系数估计的4倍，说明数据存在异常值，数据呈厚尾分布时，时空地理加权分位数回归模型比时空地理加权最小二乘回归模型效果表现更好，估计结果更为准确也更为稳健。

4 实证分析

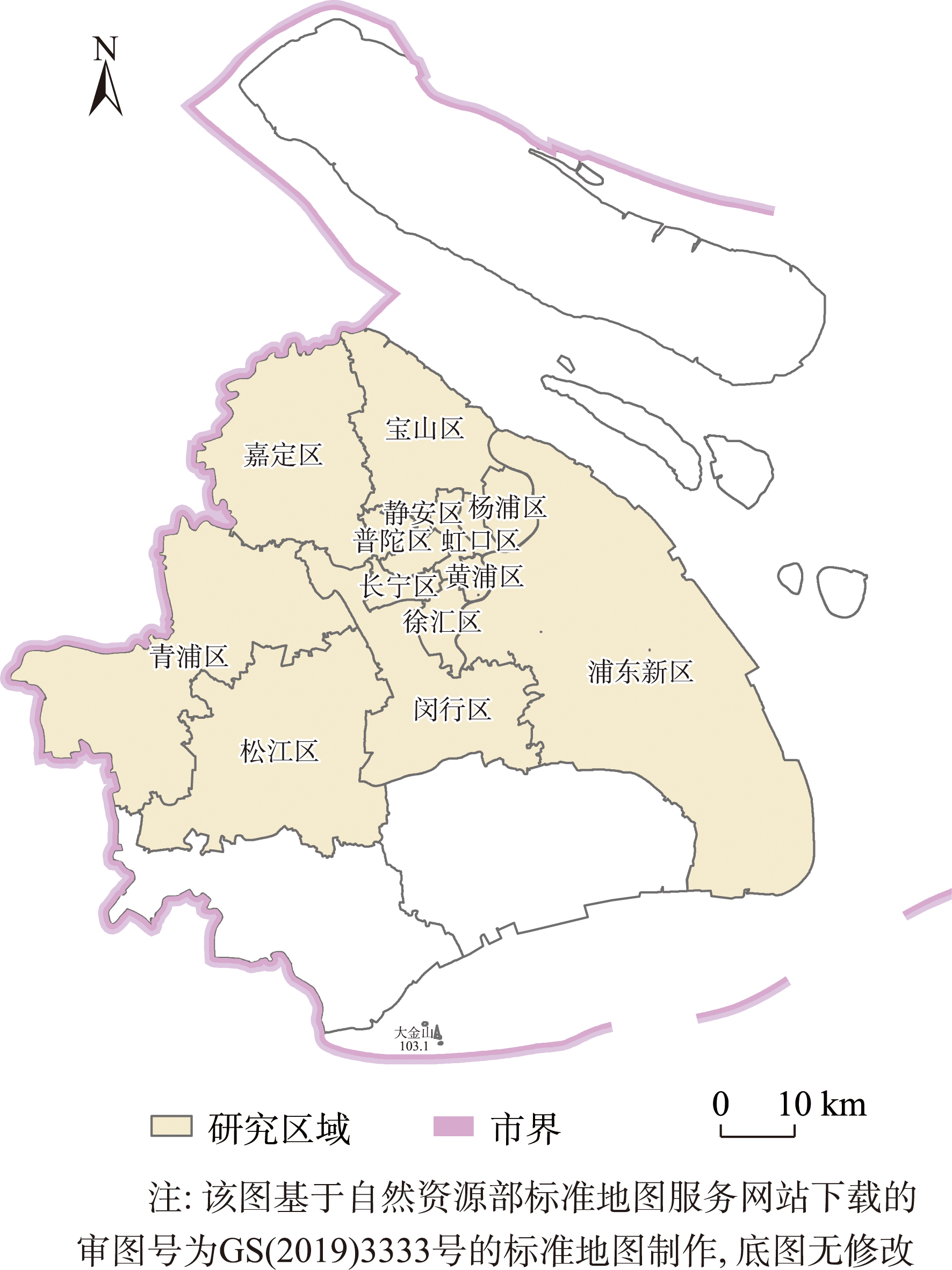
本文以上海市住宅价格时空分布格局与影响因素关系作为研究对象，通过时空地理加权回归的分位数回归模型研究分析上海市住宅价格的影响因素、每个因素如何影响住宅价格、不同分位数的住宅价格（高房价、中等房价、低房价）的影响因素及影响效果是否相同。作为我国的典型超大城市，上海的住宅市场一直备受关注，本文以上海市中心城区及商品房住宅交易活跃的郊区为主要研究区域，包括黄浦区、静安区、徐汇区、杨浦区、虹口区、长宁区、普陀区、宝山区、嘉定区、青浦区、松江区、闵行区及浦东新区13个区，如图2所示。

图2 研究区域

5 结论与讨论

5.1 结论

首先，本文基于局部多项式估计和分位数回归，提出了基于多带宽局部多项式的时空地理加权分位数回归模型，且允许不同自变量拥有不同的最优带宽。局部多项式估计相比核估计边界估计更准确，且多带宽可以处理不同自变量的时间异质性和空间异质性。基于加权最小二乘估计的时空地理加权回归方法对异常值不稳健，而分位数回归受异常值影响较小，相比最小二乘回归更为稳健且应用条件相对更为宽松。此外，分位数回归最重要的优点在于可以探索解释变量与响应变量分布的影响关系(如响应变量的多个分位数)，可以挖掘到更为丰富的信息，而最小二乘回归模型只能研究解释变量与响应变量条件均值的关系。本文基于局部多项式估计，利用两步迭代估计法给出模型的系数估计。

其次，本文通过数值模拟，将本文的分位数回归模型与时空地理加权最小二乘回归进行对比，结果显示，基于分位数回归的系数估计的均方误差和平均绝对误差均比最小二乘估计量小，比如，在0.75分位数，基于最小二乘回归得到的系数估计的均方误差和平均绝对误差分别是基于分位数回归的10倍和4倍，说明了分位数回归具有稳健性且可以研究影响响应变量分布的因素。

5.2 讨论

尽管分位数回归相比最小二乘回归更为稳健且应用条件相对更为宽松，但在数据满足高斯-马尔可夫条件时，最小二乘估计是最优估计，若此时仅仅想研究响应变量y的平均水平，不关注其全局分布（不同分位数），那么应该使用基于最小二乘估计的MGTWR。如果想探索响应变量不同分位数水平的影响因素，则需要利用本文的多带宽局部多项式GTWR分位数回归模型。此外，Lu等考虑了距离度量-参数对应的GWR模型，为不同变量选择不同距离度量和空间带宽，在之后的研究中也可以考虑在本文多带宽GTWR分位数回归模型中加入不同距离度量，以便更好地处理不同分位数下不同变量的时空相关性。