1 引言

Triple collocation（TC）方法是一种通过3个独立观测样本两两比对来估计3个样本各自不确定性的数据评估方法。与其他常见的评估方法不同，其他方法一般需要一组较为准确的实测数据作为参考数据，并将其他数据与这组参考数据进行对比。然而，获取这组参考数据通常需要较大的成本并且其自身也会存在一定的误差。TC方法通过假设了一个同时与3个样本线性相关的序列，并将其视为真值。将每个样本的误差分为对于"真值"的线性偏差与随机误差，从而在两组不相关性假设的前提下，使用严格的数学方法估算出每个样本各自的不确定性[1-3]。受求解的限制，真值序列与线性偏差是不可直接解出的，一般使用随机误差的方差var(ε_i)的大小来衡量各样本的不确定性。TC方法的计算结果可为其他数据同化或校准方法提供参考[4]，或独立地进行数据融合或校准工作[5]。这种方法在地球科学和遥感等领域具有广泛的应用。

2 基本假设

Gruber等[7]系统总结了TC方法所需的5条基本假设，并被后续研究广泛引用：

2.1 误差形式假设

误差形式假设是TC方法的出发点。其假设1个与3个样本都线性相关的"真值"序列符合如下关系：

式中：α_i，β_i为3个样本各自关于"真值t"的线性误差的系数；ε_i为3个样本各自的随机误差。

2.2 平稳性假设

平稳性假设并非是方法推导过程所必需的条件，其作用是使得方差等统计变量具有意义。Zwieback等[8]指出在不考虑对样本序列的子集仅进行二次计算的情况下，违反平稳性假设对方法结果并不会造成太大影响。在实际应用中，有研究使用滑动平均[9]、对数转换[10]、小波分析[11]等方法对样本进行预处理。这些做法不仅能使样本更好地满足平稳性要求，还能部分的消除样本与"真值"的非线性关系，使得误差形式假设得到更好地遵守。

2.3 随机误差与真值不相关

随机误差与真值不相关性假设，在差值形式的TC方法中表现为<tε_i>=0；由于E(ε_i)=0，也可写为<(t-t̄)ε_i>=0，在协方差形式中表现为cov(t,ε_i)=0，二者是等价的。共有3条：cov(t,ε₁)=0，cov(t,ε₂)=0，cov(t,ε₃)=0。

2.4 随机误差互不相关

随机误差互不相关性假设，在差值形式的TC方法中表现为<ε_iε_j>=0，在协方差形式中表现为cov(ε_i,ε_j)=0，由于E(ε_i)=0，两者是等价的。共有3条：cov(ε₁,ε₂)=0，cov(ε₁,ε₃)=0，cov(ε₂,ε₃)=0。

2.5 代表性假设

由于观测方式、观测尺度的不同，3个样本中所包含的各自的真值是存在差异的。例如在土壤水分校准工作中，站点实测、主动微波遥感、被动微波遥感这3种测量方式所得的土壤水分数据的观测尺度、采样间隔是不同的。代表性假设即假设这其中产生的所有误差均能被误差假设中的线性偏离所概括。

3 TC方法

TC方法通常有2种等价的形式：差值形式与协方差形式。差值形式的TC方法是通过3个样本之间的线性变换构造一个新的序列后，两两内积得出的；而协方差形式TC方法是通过求解协方差方程组得出的。两者在数学上是等价的[7]，其操作的核心都可看成同一种内积操作[12]。可通过协方差定义：cov(x₁,x₂)=<(x₁-x̄₁)(x₂-x̄₂)>，得出二者之间的关系。值得指出的是，即使在不相关性假设不能得到满足时，这种等价关系也是成立的。差值形式的TC方法清晰地展现了针对3个样本的变换操作及相互比对的过程。本文重点介绍差值形式的TC方法的基本原理：

首先需要有3个符合上述基本假设的样本：x₁，x₂，x₃。

根据误差形式假设（假设1）可得：

4 虚拟样本实验

由于TC方法的特点是在未知真值的情况下对数据集的不确定性进行估计，而实际数据的真值部分难以确定，使用实际数据难以检验该方法结果的准确性，也无法得知其基本假设被遵守的程度。并且在TC方法的视角下，站点实测数据也存在一定的误差，是处于方法应当进行评估与校准的范围之内，使用站点实测数据好的，我将继续输出剩余的内容，以下是论文网页可视化的续篇：

4.1 虚拟样本

对两组不相关性假设的违背程度，可以使用cov(ε_i,ε_j),cov(t,ε_i)(i,j=1,2,3，i≠j)这6个变量进行量化。当协方差为零时，即不相关，该条假设完全满足；当协方差大于（或小于）零时，即正相关（或负相关），假设不能得到满足；协方差与零的距离越大，表示相关性越强，对假设的违背程度就越大。

为了下文论述方便，将2组共6条不相关性假设对应的协方差进行编号，见表1。

表1 两组不相关性假设违背程度及下文简称

所属假设	量化违背程度的指标	下文简称
随机误差与真值不相关性假设	cov(t,ε1)	x
	cov(t,ε2)	y
	cov(t,ε3)	z
随机误差互不相关性假设	cov(ε1,ε2)	a
	cov(ε1,ε3)	b
	cov(ε2,ε3)	c

4.2 实验设计

为了分析不同不相关性假设违背对结果误差的影响，本文利用控制变量法，每组实验保持5条不相关性假设得到遵守，其中1条不相关性假设由最大负违背逐渐变化至不违背，再逐渐变化至最大正违背。即5条假设的协方差为0，1个假设的协方差由最大负值变化至最大正值。为了下文论述方便，将唯一在变化的假设称为实验变量。

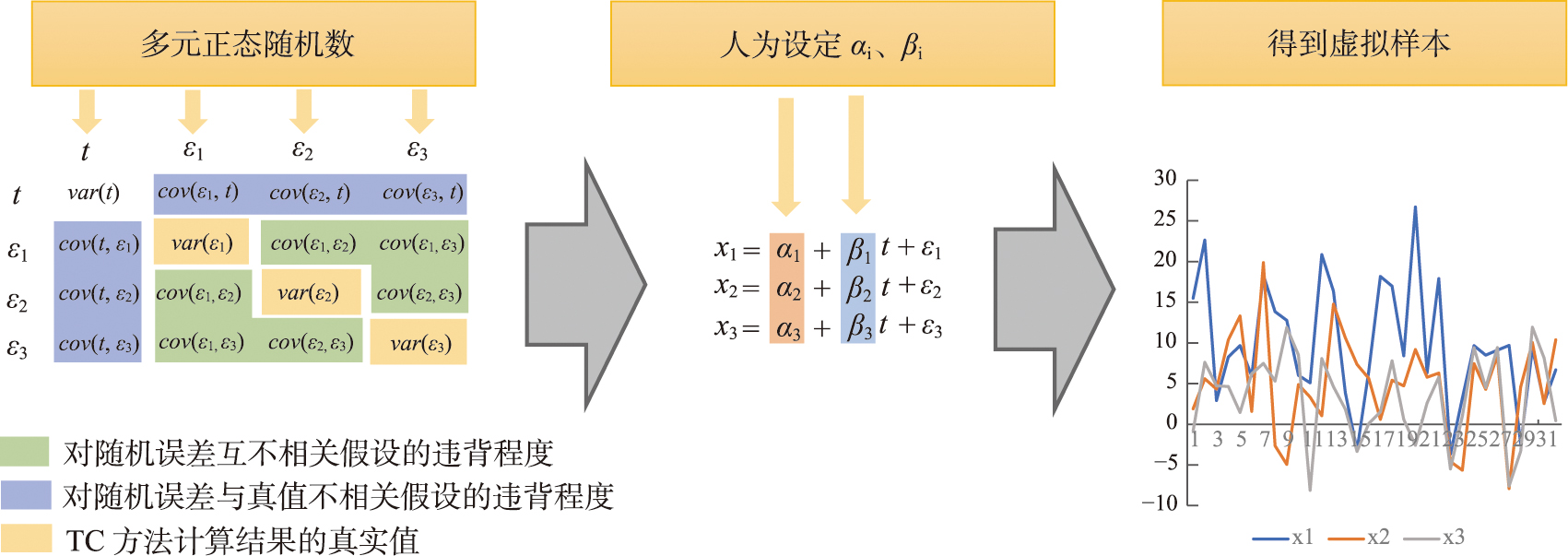
图1 虚拟样本制造过程

5 数学模拟及分析

5.1 结果误差与假设违背程度的关系

本文尝试推导出结果误差与假设违背程度的关系，从理论上对上文虚拟样本实验结果进行解释。Yilmaz等[6]通过数学推导将以x_i=β_it+ε_i为误差形式假设的TC方法的结果误差分为3类：真值泄漏误差，违背真值与随机误差不相关性假设的误差，违背随机误差互不相关性假设的误差。

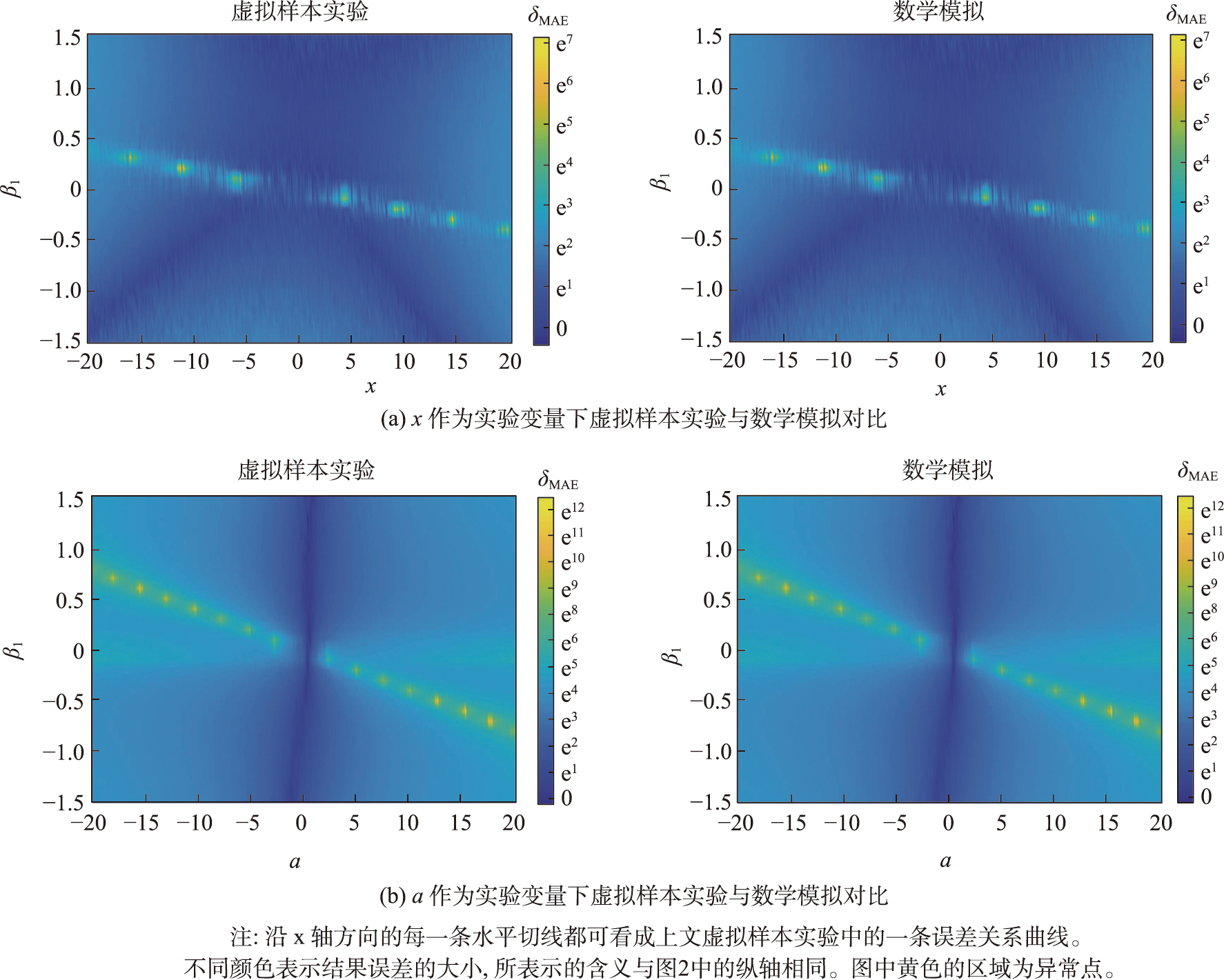
图2 虚拟样本实验与数学模拟对比

5.2 异常点出现的原因

根据式（15）—式（23）可知，假设违背程度x、y、z、a、b、c值对TC方法结果误差的影响呈现非线性关系。整体来看，可以将这种关系视为一个分式结构。当分母接近于0时，分子并不会随之接近于0，这导致结果误差会突然大幅度增加，这就是虚拟样本实验中的异常点出现的原因。

6 讨论

6.1 异常点带来的影响

以往的研究通常默认对2组不相关性假设的违背程度与结果误差之间的关系是单调的；即认为随着假设违背程度的增加，结果误差是增加的。这种思想往往会体现在2个方面：①在选取样本时，通常认为只要样本能较好地满足独立性，TC方法的误差就能控制在合理的范围内。

6.2 抑制异常点的方法

异常点的存在影响了TC方法的可靠性。消除异常点的方法，在于如何消除误差中的分母。这个分母是由缩放系数所产生的。

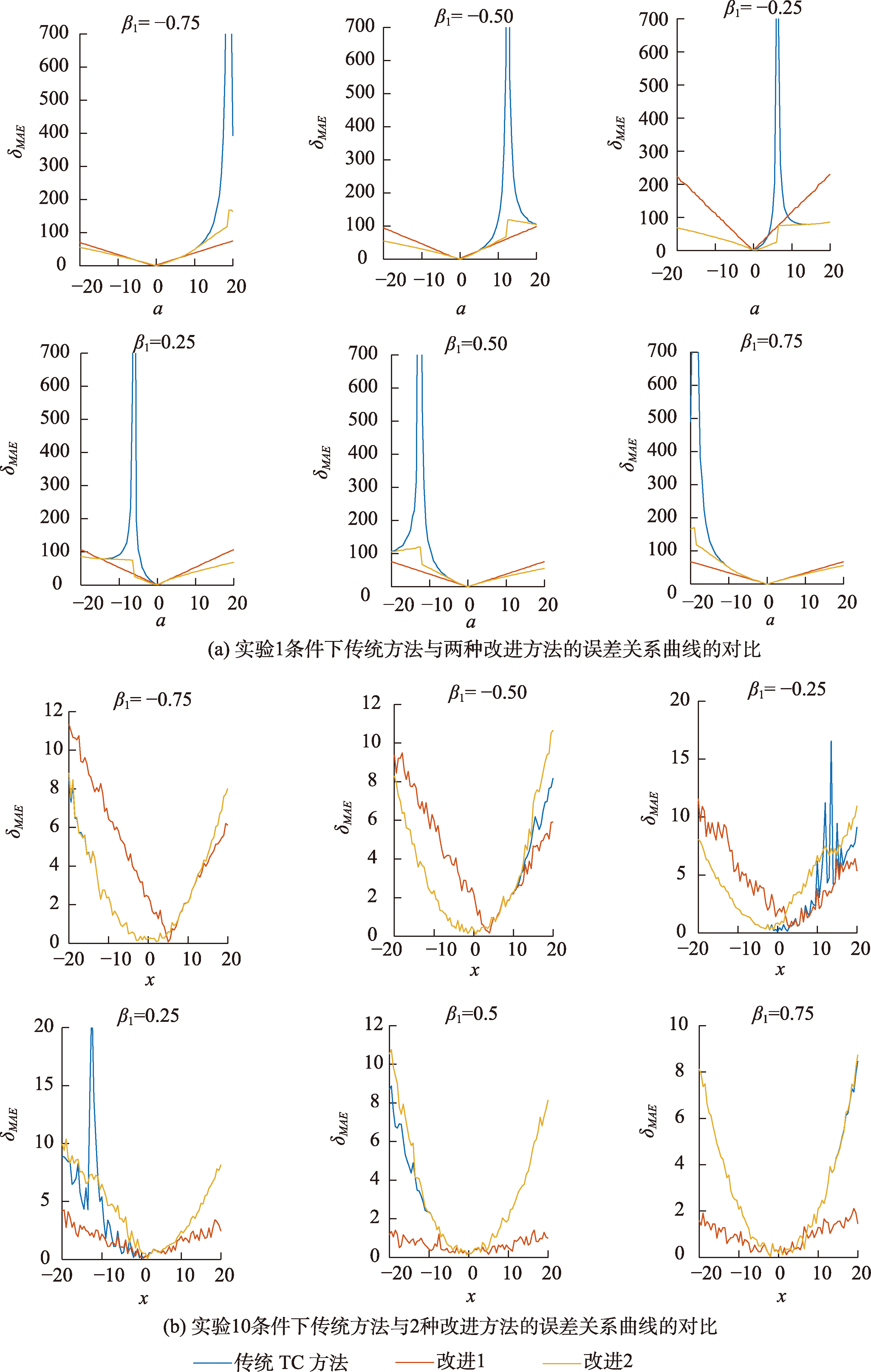
图3 2种改进方法的误差关系曲线的对比

6.2.1 忽略加性偏差系数（改进1）

使用样本均值之比代替式（3）中的缩放系数，将其改为不受不相关性假设所影响的形式。

6.2.2 限制缩放系数的上下界（改进2）

缩放系数的分式结构带来了结果误差的分式结构，限制缩放系数的上下限，使其不出现异常增大或接近于0，也可抑制异常点的出现。

6.3 出现异常点的概率

异常点是由多种参数共同作用了产生的一种特殊情况。在实际应用中，极端误差出现的概率决定了TC方法稳定性的强弱，也是衡量上述改进方法好坏的重要指标，值得进一步地讨论。

表2 各情景下误差概率分布(%)

概率	情景1	情景2	情景3
P(δMAE>30)	29.56	29.20	29.24
P(δMAE>100)	6.76	6.50	6.88
P(δMAE>200)	3.27	3.20	3.06

6.4 实测数据验证

选取SMOS,SMAP, AMSR2三套独立的遥感土壤水分数据作为TC方法的输入，使用2016—2022年ISMN站点数据进行验证。

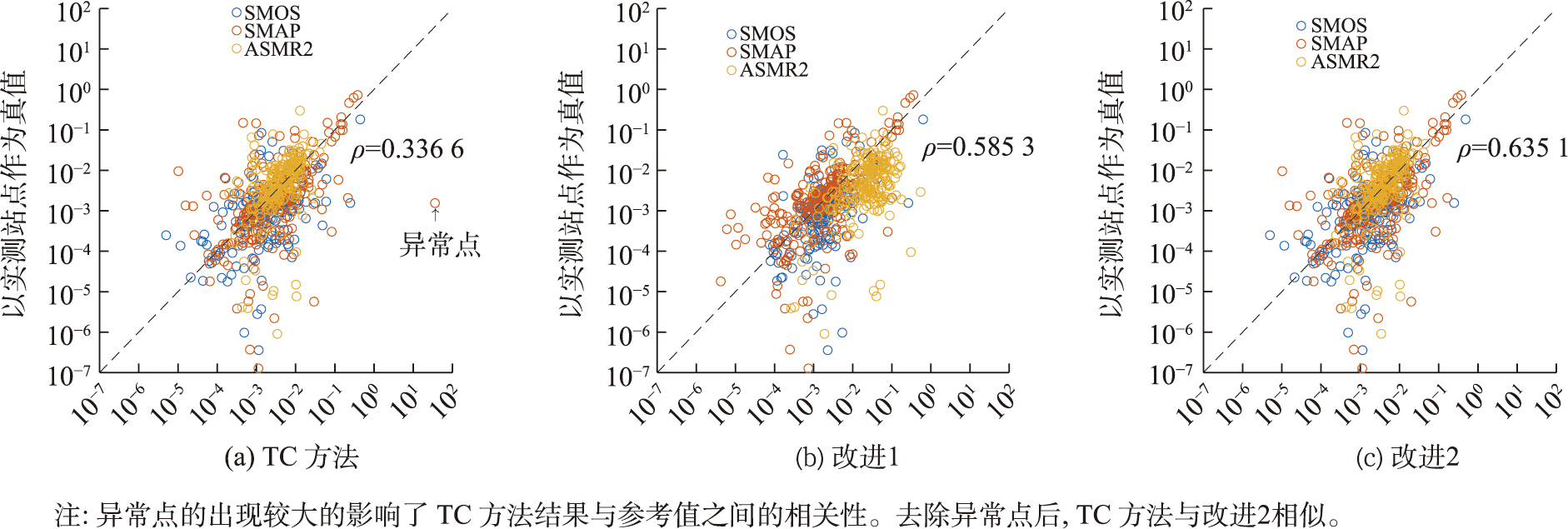
图4 TC方法、改进1、改进2与参考值的相关性对比