1. 引言
受限于衍射极限、调制传递函数、信噪比等因素的影响,遥感系统对地观测成像时难以同时兼顾理想的空间分辨率、光谱分辨率和时间分辨率,为了解决应用场景对光谱、空间、时相等多维丰富信息需求的矛盾,遥感图像融合技术应运而生。其中,全色图像与多光谱图像融合是最具代表性的应用之一,可以实现光谱信息与空间信息的优势互补,最终获取空间分辨率高、光谱信息丰富的融合图像。
2. 研究方法
本文方法技术路线图如图1所示。首先,预处理,将多光谱图像上采样,全色图像波段复制和直方图匹配预处理。其次,高斯低通滤波参数估计,考虑多光谱上采样图像合成的亮度分量图像和全色图像高斯滤波退化图像的局部方差图像,计算两者间的互信息,依据相似度最大原则进行最优高斯滤波参数估计。再次,细节图像获取,将最优高斯滤波器作用于预处理后的全色图像,得到低分辨率图像,将各波段对应的高低分辨率图像比值处理得到细节图像。然后,迭代计算细节注入系数,在高分辨率全色图像平均梯度的约束下,得到最优细节注入系数。最后,基于SFIM模型,将多光谱图像、细节图像和最优细节注入系数联合,得到融合的高分辨率多光谱图像HMS。
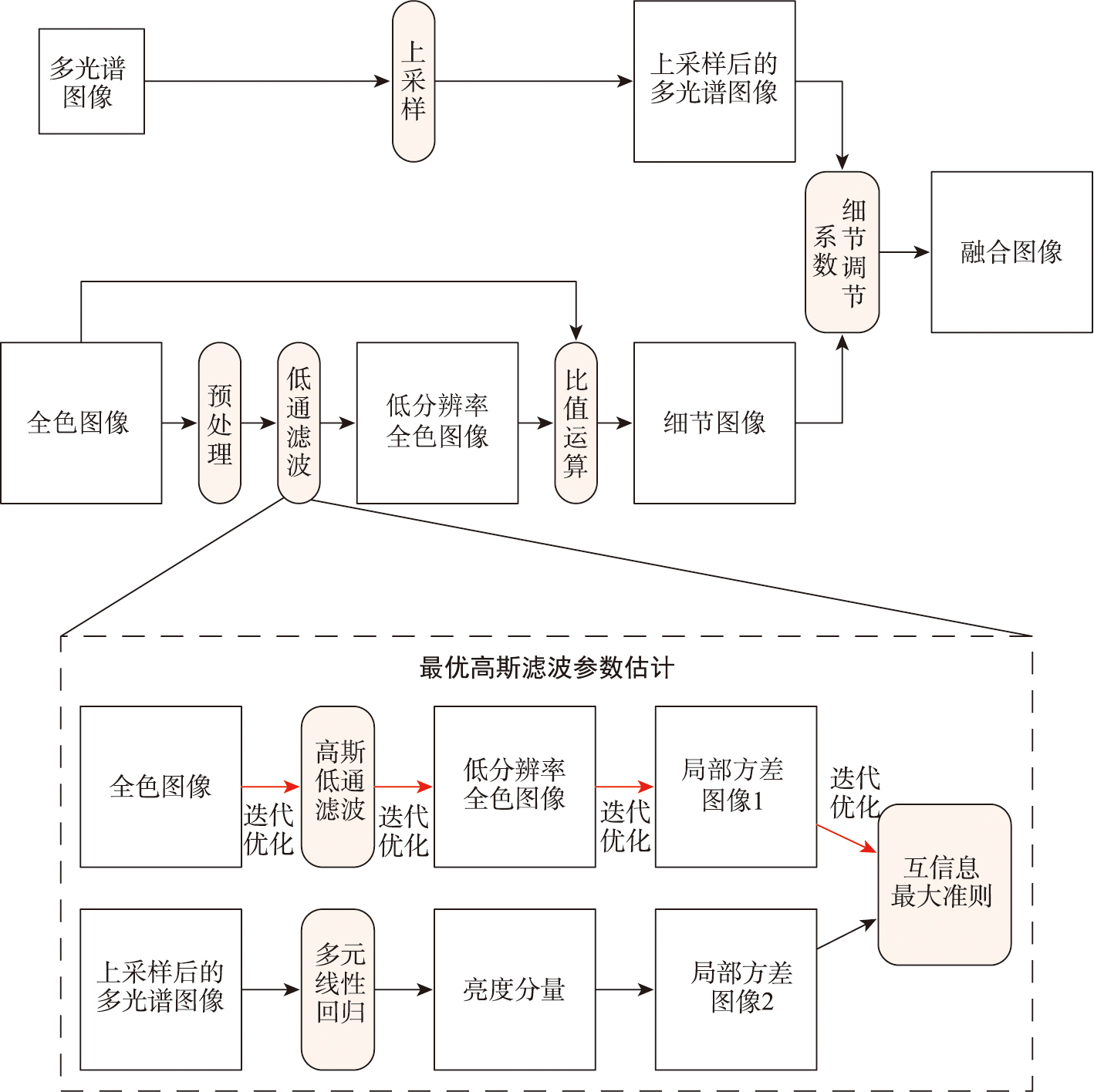
图1 本文方法基本流程
2.1 SFIM模型
图像融合过程中,基于波段间比例的空间细节注入可以较好地保持光谱信息。SFIM模型通过多光谱图像和细节注入量的乘积计算融合图像,波段间比例保持不变,聚焦于解决空间信息的融入问题,确保了模型的光谱保持能力,是一种高保真的图像融合方法。融合模型为:
HMS = MSup ∘ (P / (PL + eps))
2.2 局部方差互信息的高斯滤波参数估计
通常,PL可由全色图像P经过低通滤波得到,但在低通滤波时将涉及2个关键问题:①使用何种低通滤波器;②如何衡量滤波后图像PL与MSup在空间尺度上的一致性。
2.3 梯度一致性约束的最优注入系数计算
不同的图像有不同的空间结构特征和光谱信息,从而对细节注入量有不同的要求。细节注入越多,融合图像结构特征越清晰,但其光谱信息可能会失真;细节注入越少,融合图像光谱信息得以保持,但可能不够清晰。这说明融合图像光谱信息和空间信息的平衡可以通过控制细节注入量来实现。
3. 实验及分析
3.1 实验数据
为验证本文方法的有效性,采用Meng等制作的数据集,包括IKONOS、Quickbird2种卫星数据类型,以验证方法对不同卫星数据类型的适应性。KONOS数据的多光谱图像空间分辨率为4m、全色图像空间分辨率为1m;Quickbird数据的多光谱图像空间分辨率为0.61m、全色图像空间分辨率为2.44m。2种卫星数据全色均为1个波段,尺寸为1024×1024;多光谱图像为4个波段,尺寸为512×512。此外,对于每种卫星数据类型,根据不同地物覆盖类型,分别选取了植被、建筑、不同地物混合的3类场景,以验证方法对包含不同内容的图像融合的有效性。
3.2 实验结果分析
在融合结果评价上,分别从定性和定量两方面进行分析。定性评价方面,将多光谱图像实验结果合成真彩色显示,便于从视觉角度直观的观察光谱信息的保留情况;在此基础上提取梯度信息,通过梯度图显示不同融合结果细节的差异。需要说明的是,结果图为原始尺寸按比例缩小图,红色框中为图中局部区域的实际比例。定量评价方面,从光谱保真度、空间信息保持度、图像清晰度和信息的丰富程度4个角度,选取了光谱角映射(Spectral Angle Mapper,SAM)、空间相关系数(Spatial Correlation Coefficient,SCC)、平均梯度和信息熵EN(Entropy,EN)作为评价指标。

图2 IKONOS数据植被区不同方法融合结果

图3 IKONOS数据建筑区不同方法融合结果
3.3 最优高斯滤波参数估计分析
在IKONOS和QuickBird2种不同传感器Pi,L遥感图像生成中,MTF-SFIM方法的高斯滤波器参数为[41×41,0.17]和[41×41,0.15];AGSFIM方法高斯滤波器的参数为[3×3,0.1]和[3×3,0.63];本文提出的基于方差图像互信息的高斯滤波参数估计方法,计算出滤波器的参数为[9×9,0.7]和[11×11,0.3]。需要说明的是,本文的高斯滤波器采用了与MTF-SFIM方法中相同的kaiser窗和窗口系数处理方式,以加速参数的求解。
4. 结论与讨论
针对多光谱图像和全色图像的融合问题,本文提出了一种改进的SFIM遥感图像融合方法,该方法结合了梯度域局部方差互信息的高斯滤波和梯度一致性的自适应细节注入。主要工作如下:
主要创新点
- 提出基于局部方差图像互信息的高斯低通滤波参数估计方法
- 在保留SFIM模型光谱保真优点基础上引入细节调节系数
- 实现了光谱信息和空间信息的动态平衡
应用价值
- 特别适用于植被比例较高的场景
- 在光谱保持、图像清晰度和信息丰富度方面表现优异
- 为遥感图像融合提供了新的技术思路
未来研究方向
本文方法充分考虑了待融合图像的场景,依据场景内容动态确定高斯低通滤波的参数,进一步提高了SFIM模型的光谱保持能力。同时,在平均梯度和信息熵两个指标上,也取得了较为不错的结果。依据图像场景计算高斯滤波参数得到的图像提高了其与多光谱图像在空间尺度上的相关性,但这种全局处理方式导致同波段的不同区域都使用相同的注入系数,未能充分考虑不同区域对空谱信息需求的差异。下一步将考虑与基于图像分割和深度学习卷积网络的局部处理思想相结合,以进一步提升遥感图像空谱融合质量。