1 引言
方向关系是人们用于描述地理空间的基本空间关系之一,也是空间信息科学研究的重要内容。将方向关系的定性描述作为查询条件,即方向关系查询,不仅符合人们空间认知的需求,而且有助于提高空间查询的效率。方向关系查询作为一种重要的地理信息检索方法,目前已被广泛地应用于数据挖掘、智能推理、地图导航、多尺度数据处理等领域。
在方向关系查询过程中,需要借助一定的模型对空间对象之间的方向关系进行计算。现有的代表性方向关系模型主要包括2D-String模型、矩形模型、统计模型、锥形模型、矩阵模型和Voronoi图模型。其中,锥形模型和矩阵模型计算简单、可查询性好,常被用于方向关系查询,但由于二者忽略了空间对象的大小、形状、以及相互之间的距离对方向关系的影响,容易造成查询结果出现偏差。
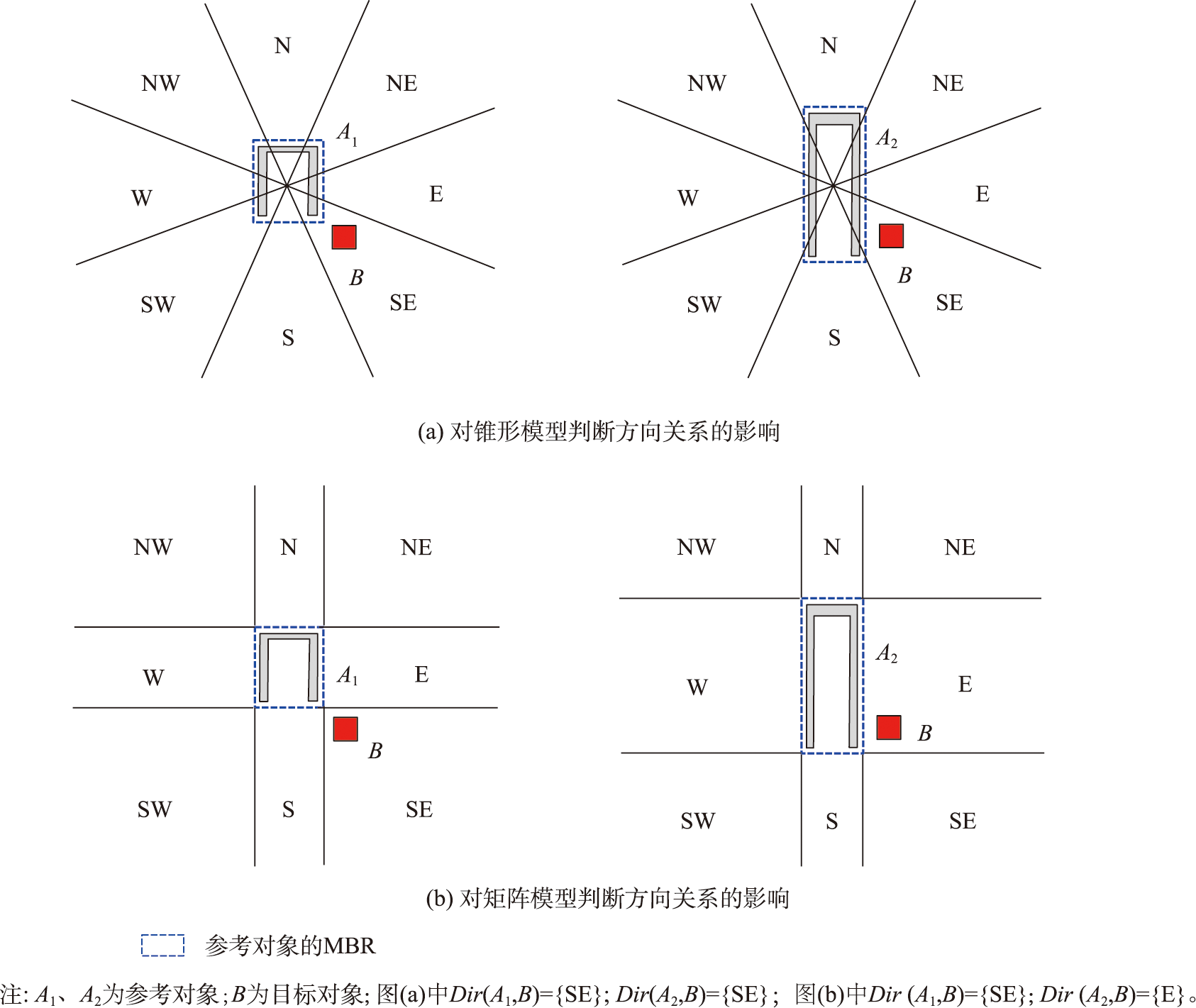
2 方向关系组合模型
2.1 基本定义
为方便论述,本文首先给出以下基本定义:
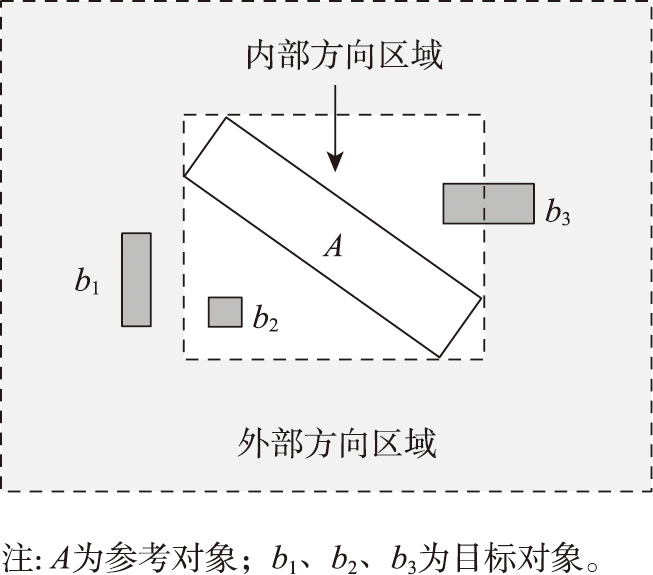
定义1 外部方向区域:参考对象A的MBR外部所占据的空间称为A的外部方向区域。
定义2 内部方向区域:参考对象A的MBR内部及边所占据的空间称为A的内部方向区域。
定义3 外部方向关系:目标对象B被参考对象A的外部方向区域包含,则规定A指向B的方向关系为外部方向关系,记为DirExternal(A,B)。
定义4 内部方向关系:目标对象B被参考对象A的内部方向区域包含或与之相交,则规定A指向B的方向关系为内部方向关系,记为DirInternal(A,B)。
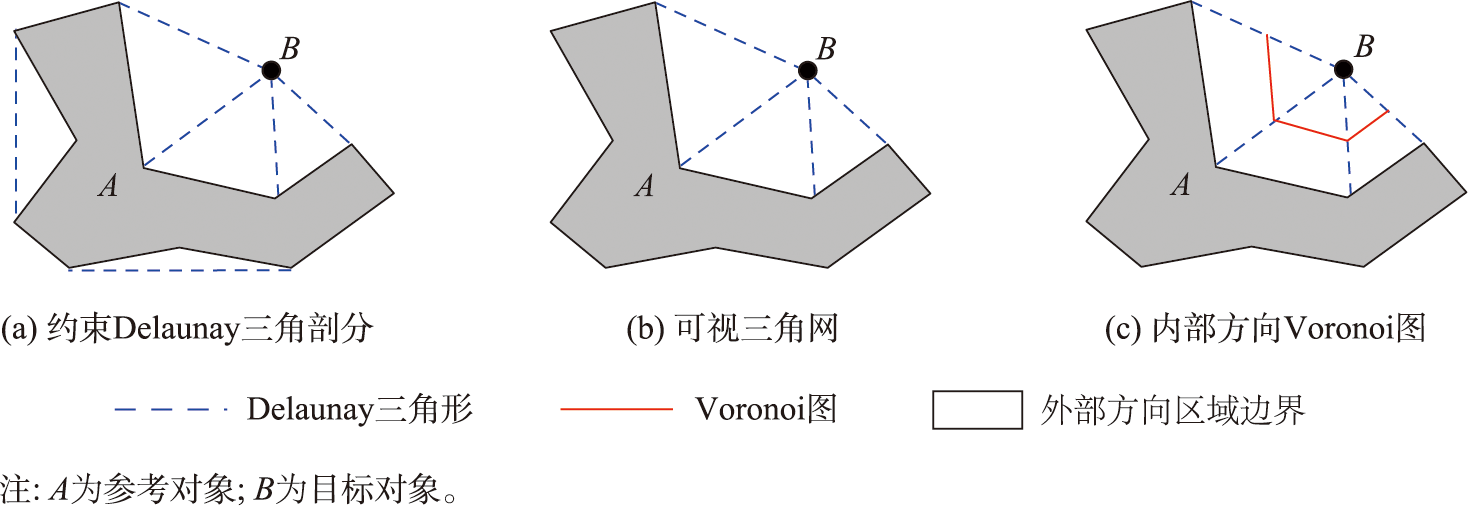
2.2 模型的构建过程
方向关系组合模型的构建包括4个主要过程:①建立外部和内部方向区域;②构建外部方向片;③构建内部方向Voronoi图;④统一描述外部和内部方向关系。
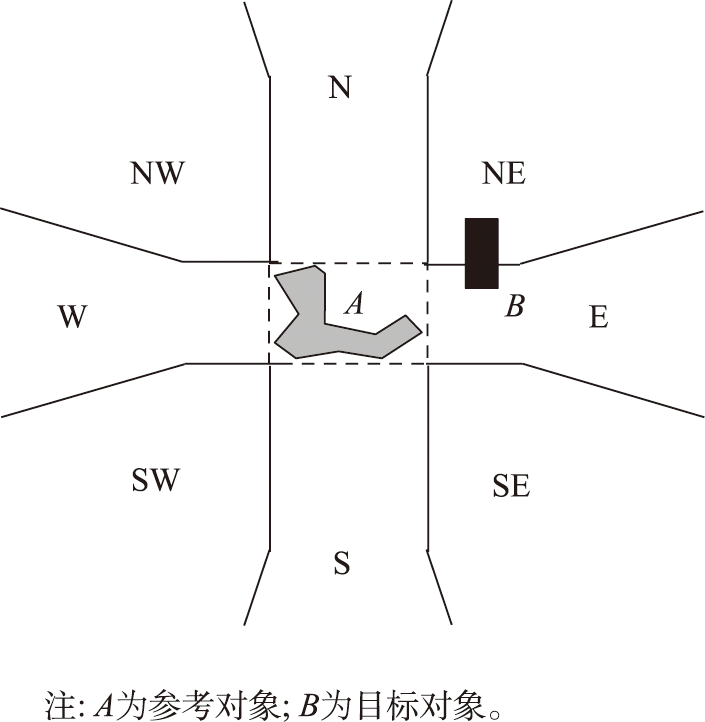
2.2.4 外部和内部方向关系的统一描述
组合模型采用8方向系统作为方向关系参考框架,并借助3×3矩阵对外部方向关系DirExternal(A,B)和内部方向关系DirInternal(A,B)进行统一描述。
3 基于组合模型的方向关系查询方法
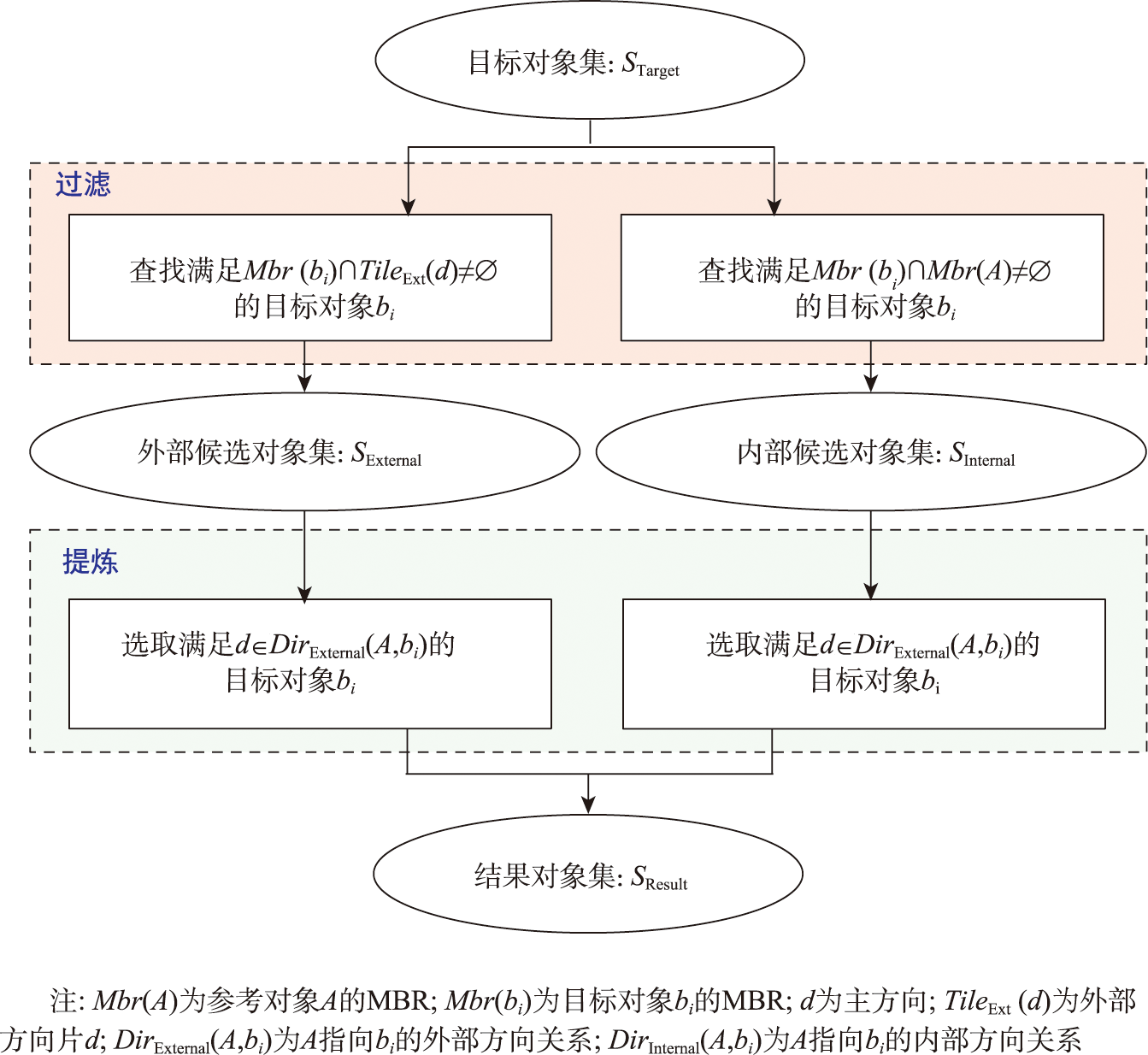
4 实验与分析
4.1 实验
4.1.1 空间认知实验
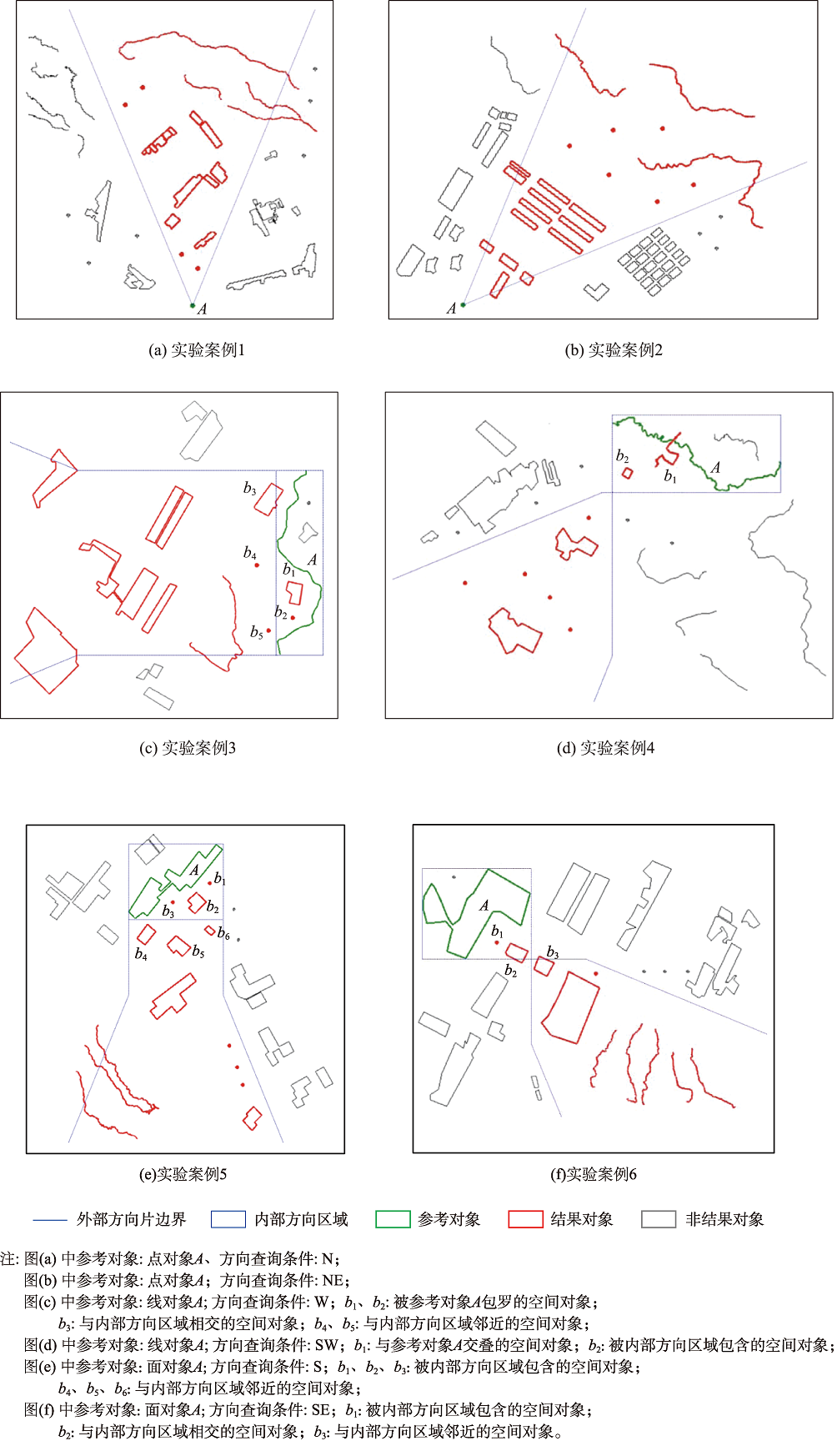
空间认知实验是检验方向关系查询准确性的一种科学且有效的手段。为了验证组合模型能够克服锥形模型和矩阵模型的不足,有效提高方向关系查询的准确性。本文选取了8组基于组合模型、锥形模型和矩阵模型的方向关系查询典型案例进行了空间认知实验。
4.1.2 地图数据实验
4.2 分析
(1)组合模型集成了Voronoi图模型的优势,能够充分顾及参考对象的形状对方向关系的影响,有效地克服了锥形模型和矩阵模型在内部方向关系查询中存在的缺陷。
(2)组合模型集成了矩阵模型和锥形模型的优势,其外部方向片能够兼顾参考对象的大小、以及参考对象和目标对象之间的距离对方向关系的影响,有效地克服了锥形模型和矩阵模型在外部方向关系查询中存在的缺陷。
(3)在8组典型实验案例中,被试对基于组合模型的方向关系查询结果的平均认可度为72.17%~82.33%,高于锥形模型和矩阵模型,这表明组合模型能够有效提高方向关系查询的准确性,其查询结果较好地符合了人们的空间认知。
(4)较之于锥形模型和矩阵模型,组合模型具有更好的适用性,不仅能够处理各类空间数据(点、线、面)之间的8方向关系查询,而且可以有效解决复杂情况下的方向关系查询问题,如包罗(图14)、缠绕(图15)、交叠(图19)等。
(5)组合模型能够对不同几何类型的地图数据进行外部和内部方向关系的统一查询,具有较好的可行性。
5 结语
方向关系查询是一种重要的地理信息检索方法。目前,在方向关系查询中使用的模型主要是锥形模型和矩阵模型,但由于二者自身的不足,容易导致方向关系查询结果出现偏差。为此,本文通过建立外部和内部方向区域,对锥形模型、矩阵模型和Voronoi图模型进行了组合,并在其基础上实现了方向关系查询。实验结果表明,组合模型具有良好的适用性和可行性,方向关系查询结果较好地符合了人们的空间认知。其主要优势是:
(1)能够充分顾及空间对象的大小、形状、以及相互之间的距离对方向关系的影响,较好地克服了锥形模型和矩阵模型在方向关系查询中存在的缺陷;
(2)能够集成锥形模型、矩阵模型和Voronoi图模型的优势,对外部和内部方向关系进行统一查询,有效地提高了方向关系查询的准确性。
该模型的不足在于其计算复杂度要高于锥形模型和矩阵模型,在实际空间查询应用中,可通过建立空间索引进一步提高计算效率。
本文提出的组合模型有助于提升空间信息智能查询、智能推理、以及多尺度空间关系相似性计算等空间数据处理方法的准确性和可信度。如何将该模型应用于上述领域,是未来研究工作要解决的主要问题。