结合三维边缘特征约束的网格模型优化方法

1 引言

基于多视图立体视觉(Multi-View Stereo, MVS)的三维重建技术利用多个视角获取的图像或视频重建三维场景。它能捕捉目标物体丰富的纹理信息，且灵活性高，适用范围广泛。因此，能够生成高精度、多细节网格模型的MVS方法一直是摄影测量和计算机视觉领域研究的关键热点。

MVS的主要流程包括多视角相机校准、图像采集、稀疏点云重建、稠密点云重建、网格模型构建、网格模型优化、纹理映射。从数据采集到稠密点云重建这些过程的现有方法均已成熟。网格模型构建是将点云数据转换为三维模型表面的关键过程。

1.1 研究背景

目前主流的网格模型构建方法有泊松重建(Poisson Surface Reconstruction, PSR)、移动最小二乘重建(Moving Least Squares, MLS)、Delaunay四面体表面重建。其中泊松重建会用曲面拟合点云数据，这种方法本身会具有一定程度的抗噪性，但是在去除噪点的同时也会损失网格模型的一部分几何细节。

在城市场景中，遮挡、反射等问题是普遍存在的。存在这种问题的区域在图像上表现为弱纹理区域。Nair等使用全局信息同时估计图像中所有像素的深度，以此推断出弱纹理区域的深度。Stathopoulou等利用图像像素上的语义标签施加特定类别的几何约束，以此填补弱纹理区域的信息空白。

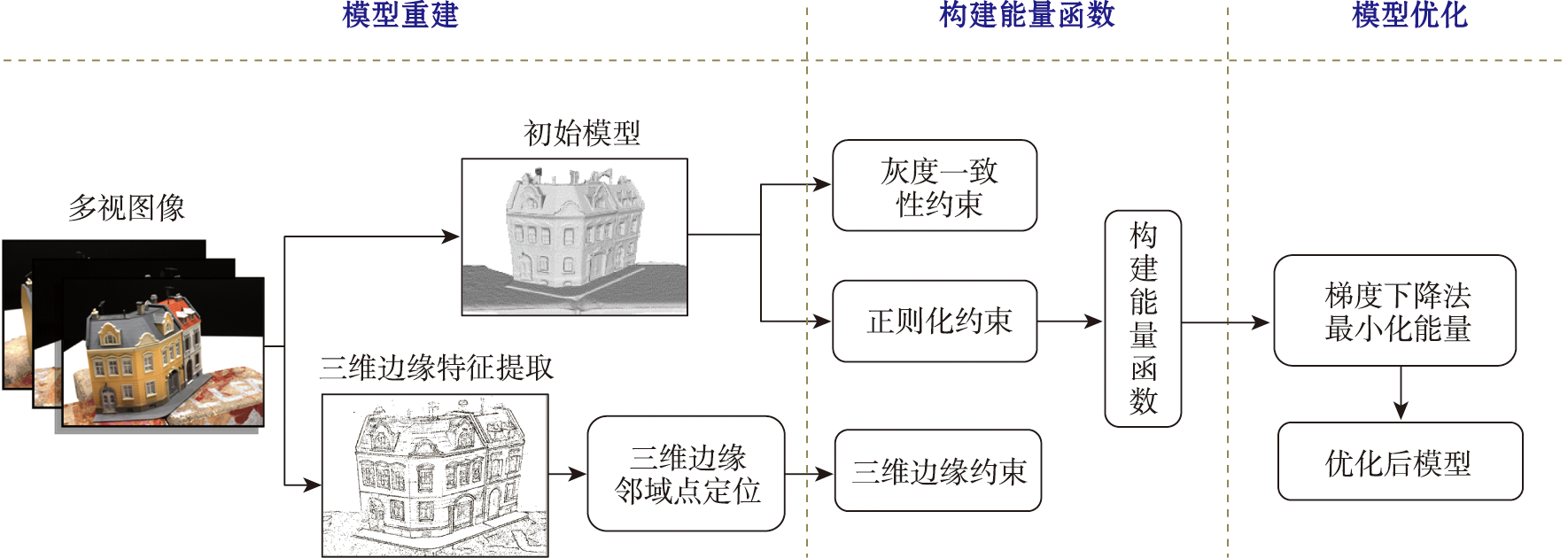
图1 三维边缘点提取结果

2 算法原理

本文在初始网格模型的基础上，利用变分原理构建能量函数，将网格模型优化问题转换为能量函数的最小化问题，驱动顶点向顶点的更优解位置移动，以此优化网格模型。算法流程如图2所示。

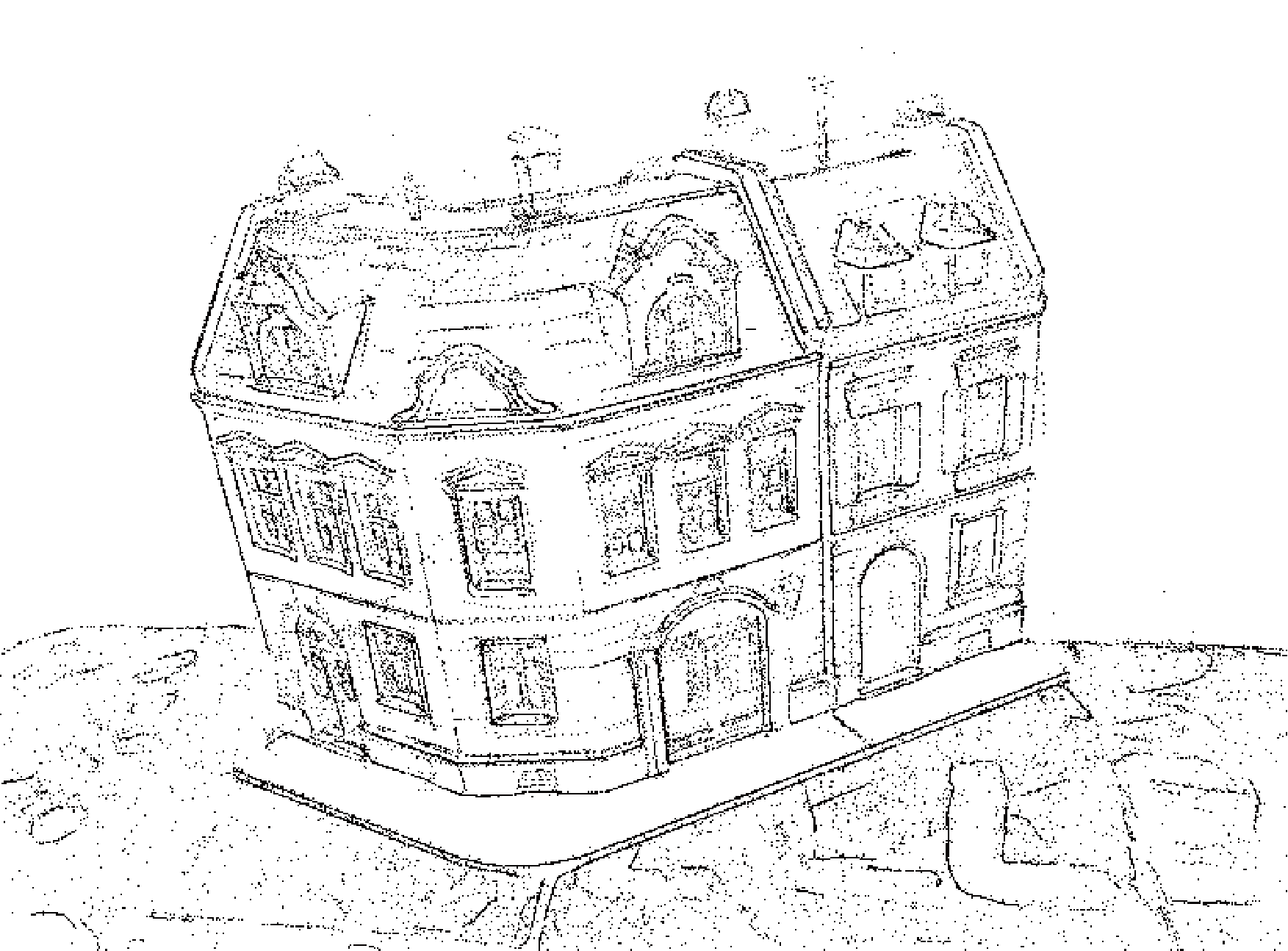
图2 网格模型优化技术路线

2.1 模型重建

本文算法以Delaunay四面体重建算法重建出的网格模型为初始网格模型，采用OpenMVS算法提供的Delaunay四面体重建方法构建网格模型，重建参数设置为默认参数。三维边缘点提取以及初始网格构建所需的初始点云由OpenMVG算法使用默认参数进行重建获得。

2.1.1 三维边缘特征提取

本文将三维边缘点集作为目标轮廓的三维表示，以此作为目标的三维边缘特征。采用文献[21]中EdgeGraph3D算法提取三维边缘点。首先使用嵌入置信度的边缘检测算法对多视图像进行边缘检测并生成边缘图像，将边缘图像中的边缘提取为二维折线边，并对折线进行平滑以匹配边缘。

2.1.2 三维边缘邻域点定位

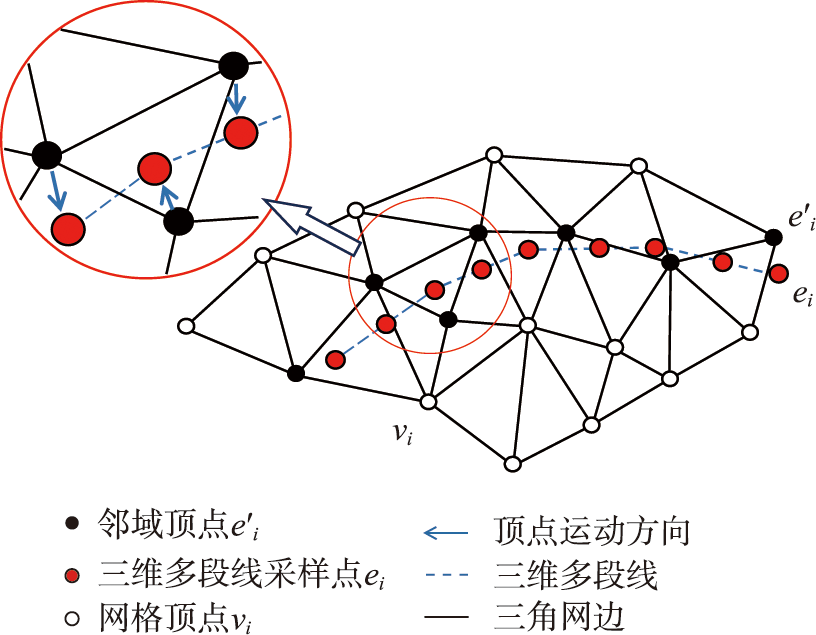
本文将从多视图像中提取的三维边缘点集表示为{e_i,i=1,2,...,X}，X为三维边缘点总数。寻找网格顶点v_i的最邻近三维边缘点e_i作为其邻域点。

图3 三维边缘点约束示意图

3 实验结果与分析

为了验证本文算法的可行性和效果，本文采用3组具有复杂几何结构的建筑物数据集进行测试，这3组数据集均包含雕塑、门框、支柱、孔洞等要素。其中前2组数据来自Strecha户外真实场景数据集，分别为Fountain-P11和Herz-Jesu-P8两个场景。第三组数据为ETH3D数据集的Relief室内真实场景。

3.1 三维边缘点精度分析

三维边缘约束的核心思想是驱动模型边缘区域顶点向更精确的位置移动，因此，本文计算三维边缘点的点位误差结果，以此作为三维边缘点精度分析基准。

表1 三维边缘点点位误差
数据	点集	MAE/cm	σ	占比/%	三维边缘点数量/个
Fountain-P11	初始网格顶点	2.48	17.18	96.7	16567
Fountain-P11	三维边缘点	0.66	9.41	97.9	16567
Herz-Jesu-P8	初始网格顶点	0.78	4.86	97.4	27390
Herz-Jesu-P8	三维边缘点	0.39	2.41	99.1	27390
Relief	初始网格顶点	1.78	11.57	95.8	38245
Relief	三维边缘点	0.91	6.12	98.6	38245

3.2 网格模型精度分析

将本文算法优化结果与MVE算法、OpenMVS算法、文献[19]算法的优化结果进行对比分析。

表2 不同方法在不同评估阈值下的评估结果
数据	方法	阈值(T_e) =2cm			阈值(T_e)=10cm
		完整度/%	精度/%	F1	完整度/%	精度/%	F1
Fountain-P11	初始网格	57.32	89.36	70.57	69.54	94.88	80.26
	OpenMVS	58.	89.99	70.89	70.04	97.50	81.52
	文献[19]算法	58.53	90.11	70.96	70.51	96.82	81.59
	本文算法	57.69	92.72	71.12	69.95	98.21	81.71

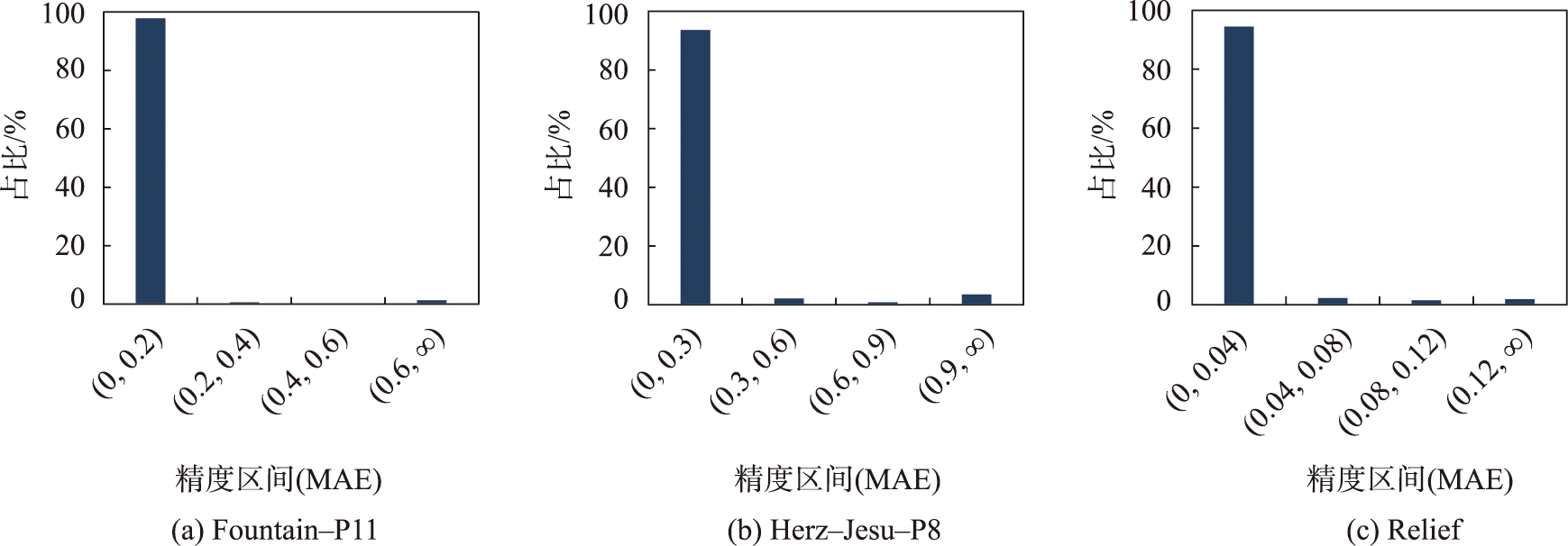
图4 不同算法优化结果对比

4 结论

城市场景三维重建过程中，边缘约束可以有效保留建筑物的边缘特征，提高重建结果的准确程度以及视觉效果。针对已有的结合边缘约束的网格模型优化方法存在对建筑物的不规则边缘作用有限的问题，本文提出一种结合三维边缘特征约束的多视立体网格模型优化方法。

将网格模型顶点向真实世界表面移动问题转换为对模型表面顶点的总体能量求解最小值问题，引入灰度一致性约束项、正则化项以及三维边缘约束项，通过梯度下降法迭代求解总体能量函数的最小值，将每次梯度的变化量应用到顶点上，驱动模型顶点产生形变。该方法具有以下优势：

本文使用三维边缘点与模型边缘区域顶点的位置差异作为模型优化的轮廓驱动力，相对于提取三维直线约束网格模型的方法，本文算法可以同时约束直线边缘与曲线边缘；
相比利用可视外壳进行约束的方法，在三维空间中对模型顶点的边缘进行约束，能够处理城市场景的复杂结构特征；
本文以网格顶点与其邻域顶点的曲率信息构建正则化约束，与三维边缘约束构成互补关系，可有效避免三维边缘约束可能造成的模型表面异常凸起或凹陷。

* 以上内容由AI自动生成，内容仅供参考。对于因使用本网站以上内容产生的相关后果，本网站不承担任何商业和法律责任。