1 引言
在信息化时代,数字三维信息的需求突飞猛进,推动了三维激光扫描技术、近景摄影测量技术、计算机视觉技术等的飞速发展,点云数据逐渐成为一种重要的三维空间信息表达方式。
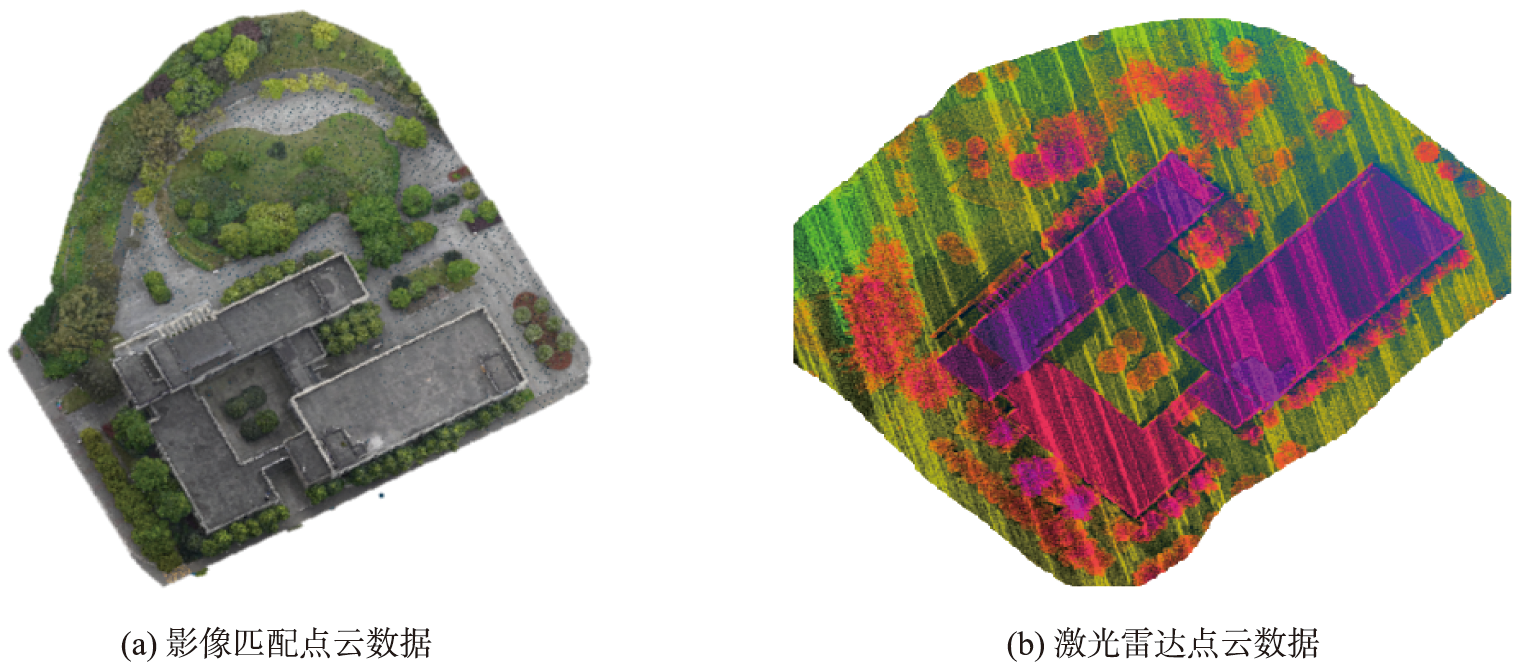
三维激光雷达(LiDAR)点云数据包含三维坐标信息(X,Y,Z),反射强度信息、回波次数信息等;但是,激光点云数据通常只在物体表面产生离散的点云,由于场景中三维物体的遮挡等问题,导致点云数据无法表示连续的三维形状,对于形成的空洞需要额外的数据或算法来补充,而且,单纯的激光点云数据不包含颜色和纹理等信息。
影像匹配点云数据(或摄影测量点云)包含丰富的纹理细节、光谱信息、边缘特征,可以在最大程度上直观还原真实场景。但受制于影像采集的质量和拍摄气候环境,影像匹配点云的精度往往不如激光雷达点云,且噪声水平相对较高。
由此可见,来自不同平台的点云都具有其独特的优势和限制,跨源点云数据的融合可以优势互补,解决单一数据存在的数据空洞、信息缺乏等问题,减少场景噪声,提高点密度和精度,实现大范围场景完整、精细的数字现实描述。
2 跨源点云配准方法描述
2.1 跨源点云配准问题定义
设源点云集P={pi}∈R3i=1N和目标点云集Q={qj}∈R3j=1M,其中pi、qj分别为两点云集中的对应点;N,M分别表示点云集中的点数。源点云和目标点云之间应满足的几何关系:
qj = s·R·pi + t
式中:pi、qj分别为两点云集中的对应点;s为尺度因子;R为正交旋转矩阵;t为平移向量。点云配准就是恢复2个点云集之间的对应关系和估算可以对齐相应点云对的最佳变换,其可以表示为一个优化问题:
Argmin ∑‖qj - (s·R·pi + t)‖2
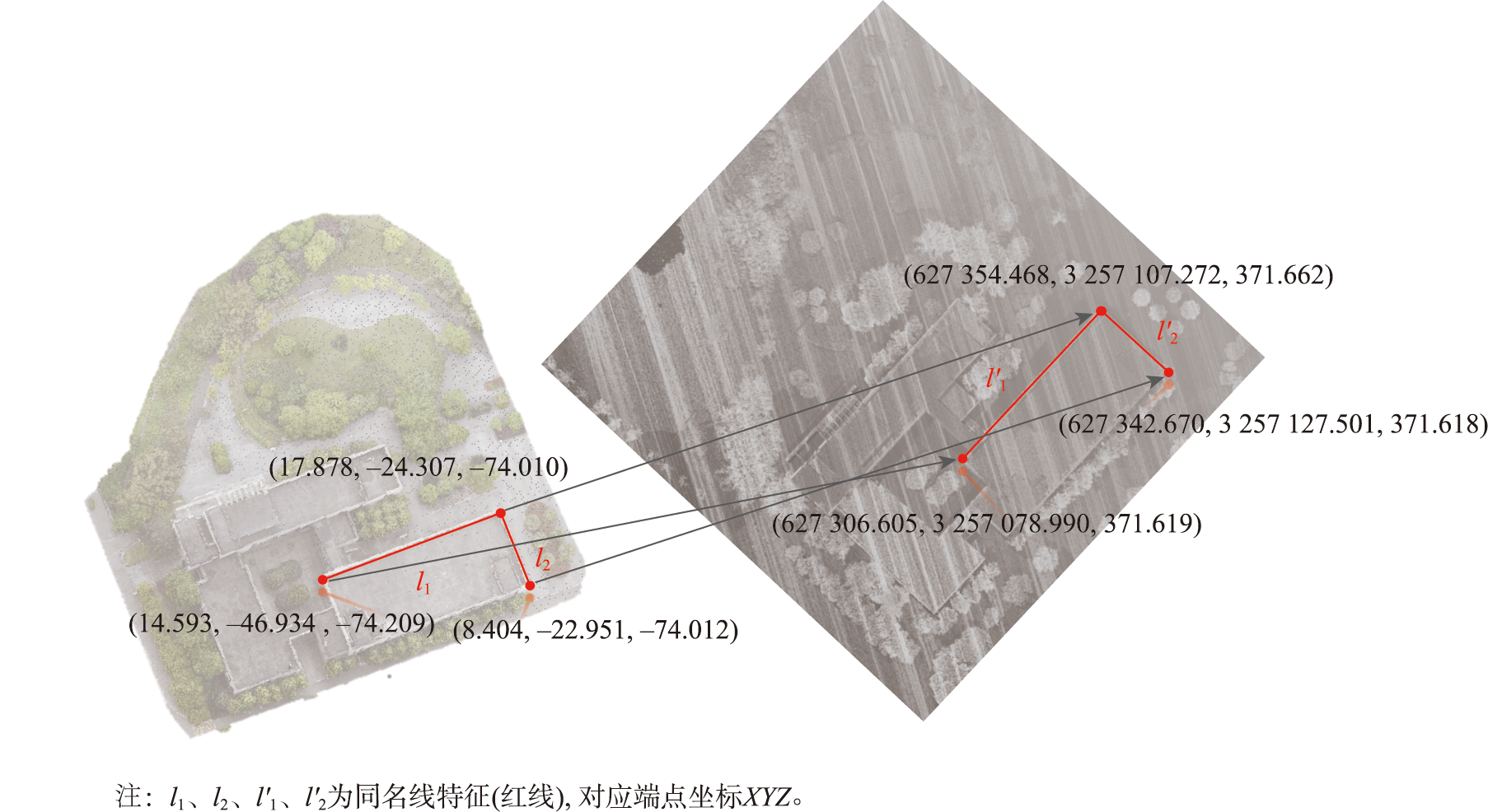
2.2 基于线特征约束的粗配准
设线段ab和AB分别为不同来源点云中的同名线,但端点并没有一一对应,基于配准原理和共线方程,2条线段存在以下关系:
式中:[Xt,Yt,Zt]T表示源点云与目标点云之间的平移参数;[Xa,Ya,Za]T、[Xb,Yb,Zb]T、[XA,YA,ZA]T、[XB,YB,ZB]T为同名点坐标;R表示旋转矩阵;s表示尺度因子;λ1、λ2为引入的未知参数。
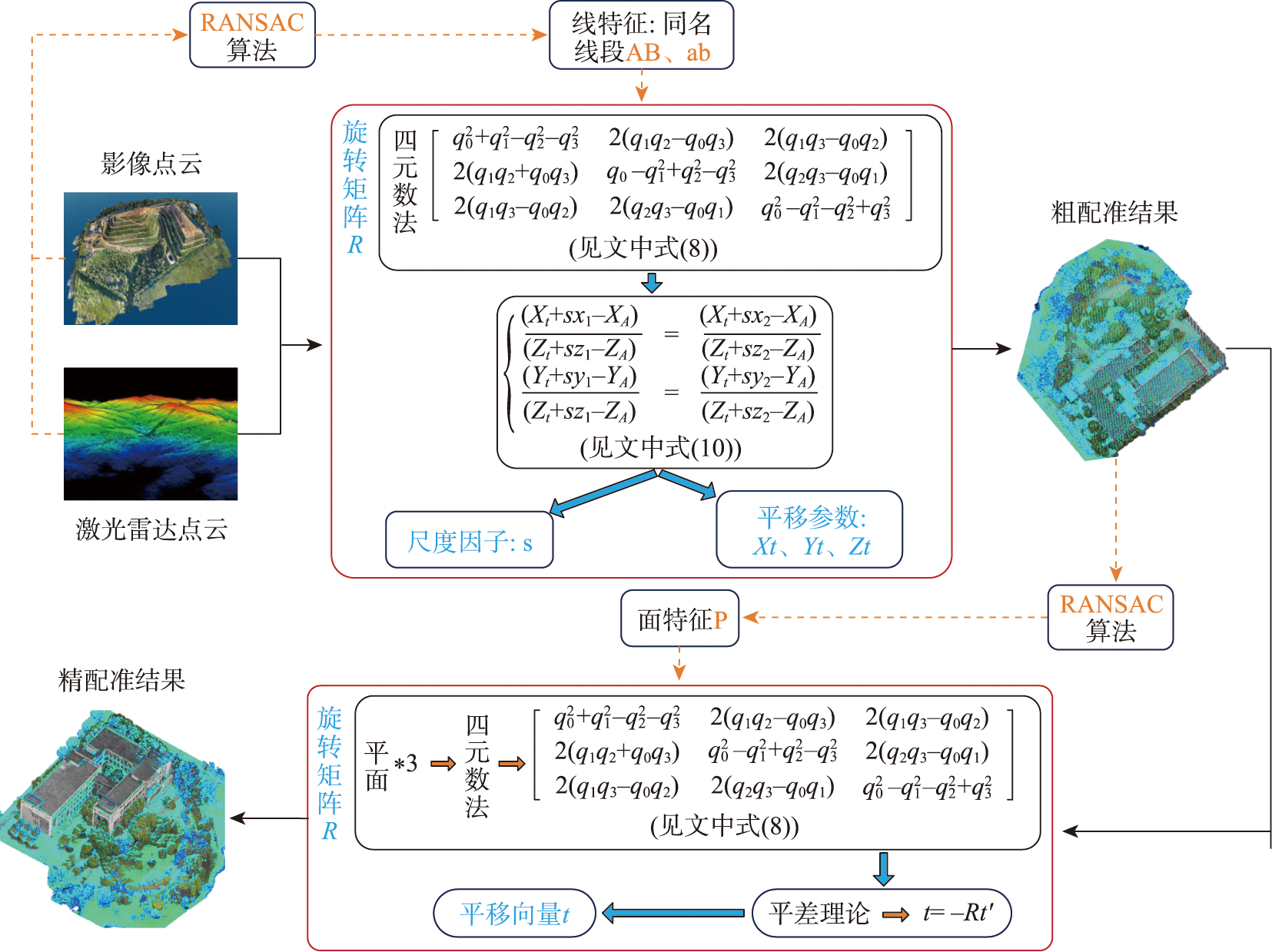
图1 线面特征约束的跨源点云配准技术流程
3 实验及结果分析
3.1 实验数据说明
实验数据是采用六旋翼无人机(型号KWT-X6L-L15)搭载Sony数码相机(ILCE-Alpha7R IV)和激光雷达传感器(RIEGL VUX-1LR)对重庆交通大学科学城校区进行采集,利用ContexCapture软件进行一系列处理得到的影像匹配点云数据和激光雷达点云数据。

图2 跨源点云实验数据
3.2 小区域单个建筑物的配准
该场景中主体建筑为校园图书馆,另外还包括周围的道路以及绿化设施。其中激光雷达点云数据包含3446175个点,影像匹配点云数据包含126472367个点。
3.5 结果分析
为了验证本文提出的算法在不同场景中的性能,采用均方根误差(Root Mean Square Error,RMSE)、配准后平面间二面角θ以及中心点到平面的距离distance_center(pi)/(qi)作为配准效果的精度评价指标。
表1 各算法在不同场景中下计算的RMSE
| 场景 |
文献[12] |
文献[17] |
本文方法 |
| 小区域单建筑 |
0.3685 |
0.5173 |
0.3647 |
| 小区域多建筑 |
0.1275 |
0.3135 |
0.0320 |
| 大区域建筑群 |
0.7026 |
0.8791 |
0.6146 |
表2 面与面的夹角及中心点到平面的距离
| 场景 |
二面角θ/(°) |
distance_center(pi)/(qi) |
distance_center(qi)/(pi) |
| 小区域单建筑 |
0.5578 |
0.117 |
0.109 |
| 小区域多建筑 |
1.3716 |
0.012 |
0.004 |
| 大区域建筑群 |
0.4164 |
0.613 |
0.604 |
4 结论与展望
4.1 结论
相对于单一的点、线和面特征,线面特征约束的点云配准强化了几何约束性,因此本文提出了一种线面特征约束下的跨源点云配准方法。通过RANSAC算法提取出同名线和面特征,通过线特征约束估算变换来完成粗配准,解决尺度差异性。
为了兼顾计算效率和精度,本文在粗配准的基础上根据面特征求解旋转矩阵和平移参数完成精配准。从RMSE值来看,在不同的场景下,本文方法对比文献[12]和文献[17]精度分别高了15.6%和40.8%。并且同名面夹角和中心点到平面的距离均符合精度要求。
综上所述,对于不同场景,基于线特征约束的粗配准能够很好地解决尺度问题,基于面特征约束的精配准进一步提升了旋转矩阵和平移参数的求解精度,说明基于线面特征约束的跨源点云配准方法是可行的。
4.2 展望
本文算法在不同尺度的跨源点云数据上的配准精度优于一些传统的算法,但仍存在些许不足。本文在精配准中没有考虑尺度的差异性,而且本方法主要依赖于线面特征的提取,如果实际场景中包含较少的线面特征,该方法将受到一定的限制。
因此在后续研究中将考虑增加点特征的约束,并在精配准中考虑尺度差异性,采用对偶四元数来求解空间变换参数,最后使用多组不同场景下的跨源点云数据进行实验验证,并采用多个评价指标对不同算法进行对比分析,以提高算法的配准精度和保证算法的鲁棒性。
* 以上内容由AI自动生成,内容仅供参考。对于因使用本网站以上内容产生的相关后果,本网站不承担任何商业和法律责任。