1 引言
空间冲突的处理是制图综合具有挑战性的难题之一。随着比例尺的缩小,地图上的符号难免发生压盖、重叠等占位性空间冲突,在执行化简、夸大等综合算子时同样易产生空间冲突。为解决化简冲突,即执行化简算子所导致的空间冲突,学者们进行了广泛的研究。传统的解决方法是先执行化简算子,然后识别空间冲突并通过移位等操作进行处理,该类方法较复杂且效率低下。
目前的主流思想是在化简过程中尽量避免产生空间冲突,不同学者避免空间冲突的手段各不相同,如Saalfeld等通过动态更新凸包结构来有效地检测和消除曲线自身及其他邻近实体的潜在拓扑冲突。Corcoran等将拓扑关系分为平面关系与非平面关系,分析了不同关系下的化简方法,并整合分析对象的优点提出了一种保持拓扑一致性的化简策略。Tienaah等以线实体及邻近实体间的拓扑与方向关系为上下文约束,通过拓展二叉树模型对Douglas-Peucker算法进行改进。李成名等通过全局化简判断模型对曲线间距较小区域处进行选择性处理以避免出现拓扑变化。张付兵等以拓扑弧段为化简单元,构建约束Delaunay三角网支持下的弧段双侧层次多叉树模型,实现面群邻接边线的协同化简。
为保持道路与居民地在毗邻区域的空间关系及视觉效果,本文以道路与居民地为对象开展顾及形状相似性的协同化简研究。首先提取道路与居民地轮廓中成对的毗邻片段,其次采用动态时间归整算法(Dynamic Time Warping, DTW)进行节点粗匹配,然后根据节点的几何特征对粗匹配结果进行优化,最后根据匹配结果进行协同化简。
2 研究方法
2.1 化简冲突分析
地图要素间的空间关系在综合前后需要尽可能保持一致,否则会影响地图的准确性与可读性。随着比例尺缩小,建筑物逐渐被合并为较大的街区,正常情况下居民地与道路相切或相离,其靠近道路的轮廓往往与道路有着较高的形状相似性,如图1所示。
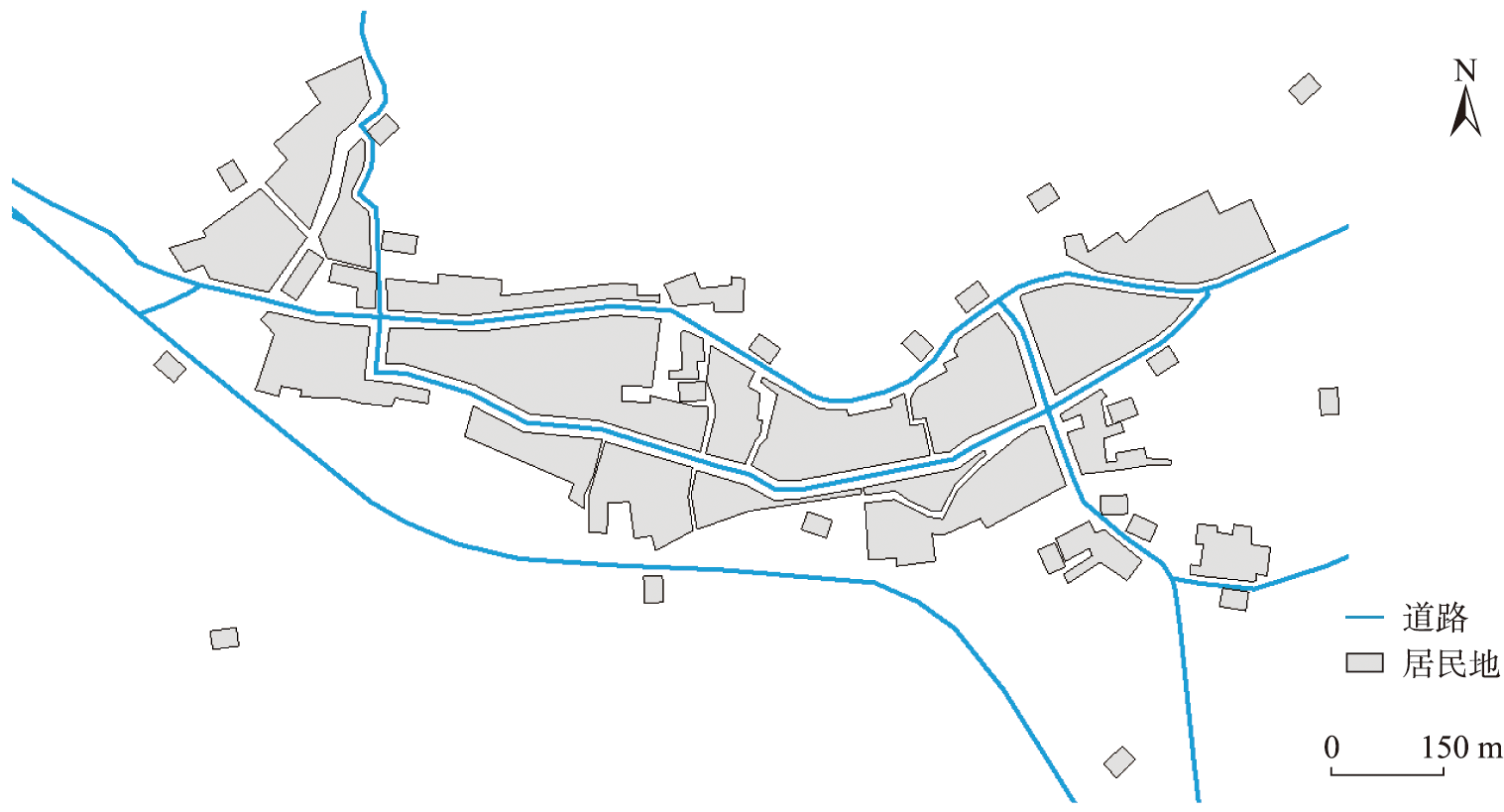
道路与居民地间的强相关性是居民地轮廓与邻近道路形状相似性的根本原因,不同研究对形状相似性的定义与描述不同。距离是评价形状相似性的基本特征,空间距离越小越均衡则越相似。角度、节点曲率、弯曲层次等也是形状相似性评价的常用特征。刘鹏程等利用傅里叶形状描述子表达形状,傅里叶级数展开越接近则形状越相似。总体而言,形状相似的道路与居民地轮廓具有较小且均衡空间距离、相似的节点角度与曲率、相近的曲折程度与近似的平行关系。
地图上的线要素由节点与连接线段构成,化简算子会改变节点的数量与位置,进而改变线要素的空间位置及整体形状。分别化简毗邻且形状相似的道路与居民地轮廓时,两种要素各自的节点变化情况互不关联,很有可能造成要素间空间关系的改变。根据道路与居民地化简冲突涉及的关系类型,可以分为拓扑冲突与形状冲突,如图2所示。其中,拓扑冲突存在拓扑错误,具体表现为"相离➝相交"。形状冲突则主要是距离关系与方向关系的不一致,具体表现为"近似平行➝显著不平行"。
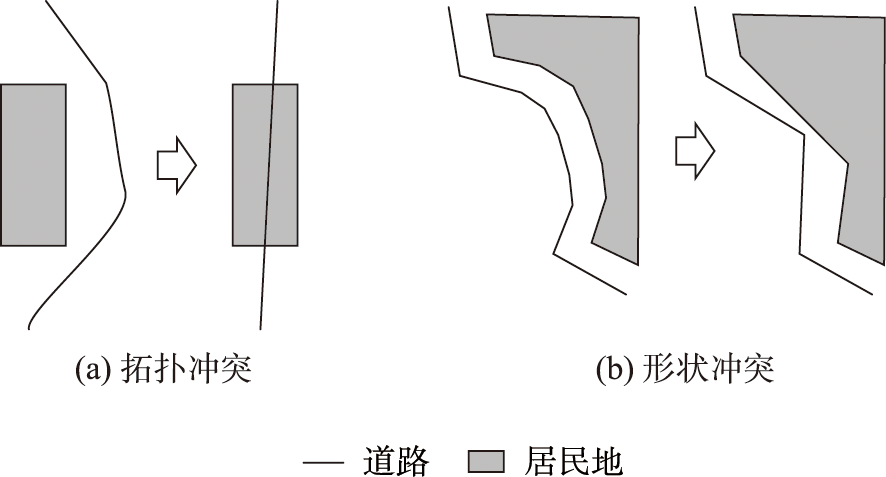
经分析,产生化简冲突的原因主要包括:①道路与居民地各自采取的参数阈值或化简算法不同;②毗邻相似曲线段各自所处的空间上下文环境不同,如化简起始点位置、前后的线要素空间分布等;③毗邻曲线段各自的细节表现不同。为避免产生化简冲突,可通过线要素节点匹配建立道路与居民地轮廓的关联关系,同步取舍其中的关键节点。
2.2 方法流程
协同化简的核心是建立道路节点与居民地节点间的匹配关系,通过节点同步取舍实现两种要素的协同化简(图3)。本文所提出的协同化简方法主要步骤如下:
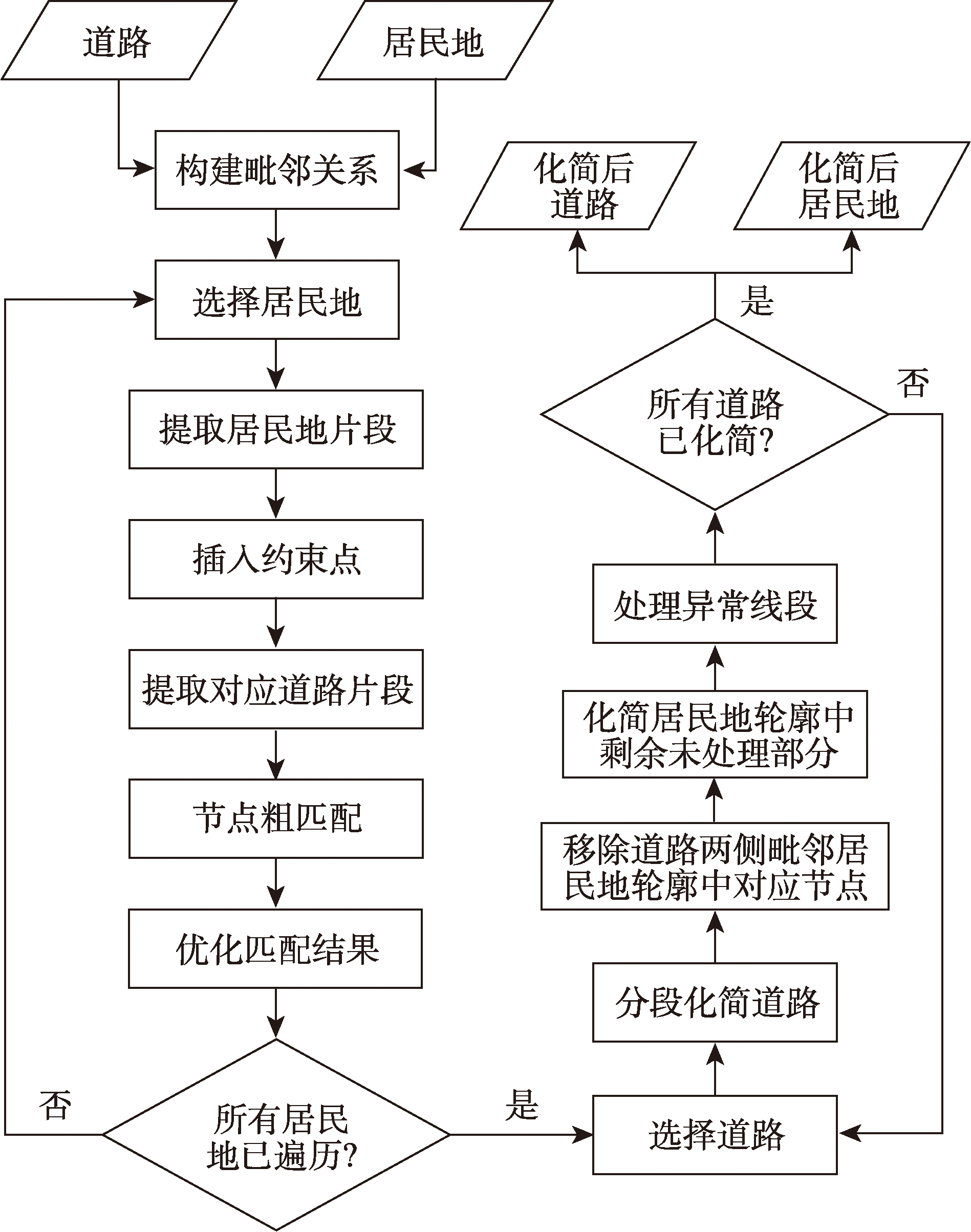
- 预处理。构建道路与居民地间的毗邻关系,将目标居民地的若干条毗邻道路连接为一条完整道路。
- 提取毗邻片段。利用Delaunay三角网提取毗邻的居民地片段,然后提取居民地片段对应的道路片段,并在该过程中插入对应约束点。
- 节点匹配。采用DTW算法进行节点粗匹配,然后结合节点及其连接线的几何特征对匹配结果进行优化。
- 协同化简。在约束点的控制下化简道路,根据节点匹配结果将道路的节点取舍同步到居民地轮廓,采用合适算法化简非毗邻区域的居民地轮廓,最后处理结果中的异常线段。
2.3 提取毗邻片段
毗邻,即边界相接,这里指居民地紧邻道路分布。若目标居民地与目标道路间的距离小于毗邻距离pd且无其他道路或居民地阻隔,则认为二者毗邻。不同居民地与道路间的毗邻状态不同,如图4所示,居民地I有一个连续片段与道路毗邻,居民地II有多个间断片段与道路毗邻,居民地III则完全与道路毗邻。
毗邻片段,即道路或居民地与对方紧密相邻部分的轮廓,是实体间最直接的关联部位。仅毗邻区域需要协同处理,成对的毗邻片段是后续处理的基础,提取居民地的毗邻片段及道路上与之对应的片段,过程如图5所示。
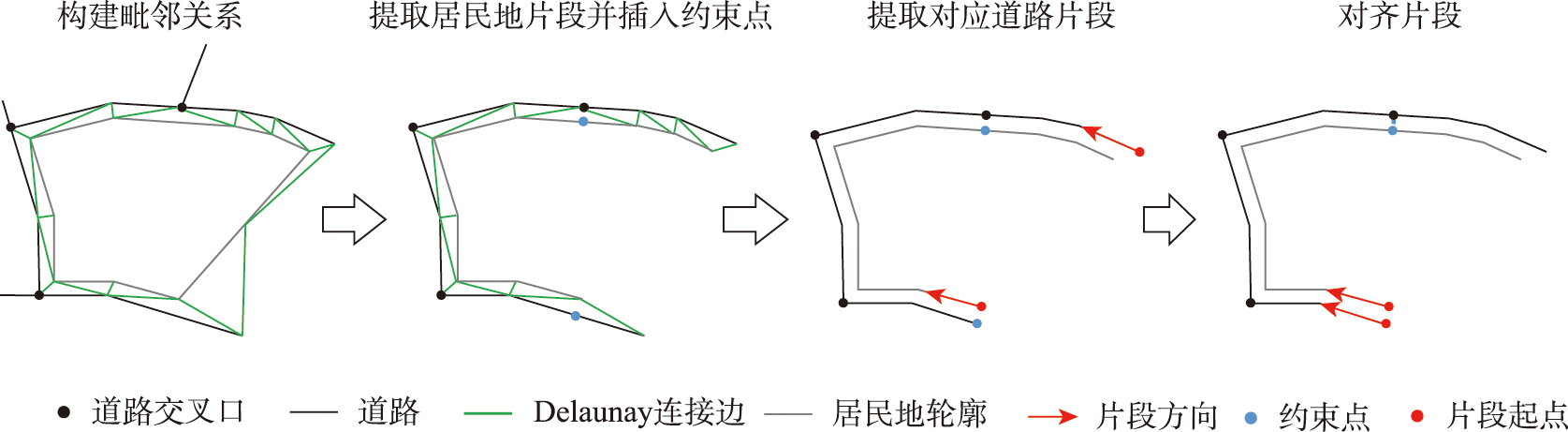
对于与道路完全毗邻的居民地,其片段与毗邻道路片段均为环状线,不需要进行裁剪,仅需调整片段的起点与方向。
2.4 节点匹配
在制图综合中,节点匹配主要应用于线面要素的Morphing变换,具体的技术手段包括缓冲区法、形状上下文、OptCor及骨架线特征等。上述方法服务于Morphing变换中的多尺度插值,匹配对象的比例尺差距大,形态详略程度不同,主要强调特征节点的匹配。协同化简需要同步取舍道路与居民地的部分节点,对匹配精度要求较高,现有匹配方法难以满足要求。因此,本文设计了一种两步匹配法以进行高精度的节点匹配,首先采用DTW算法进行粗匹配,而后结合节点与连接线的几何特征对匹配结果进行优化。
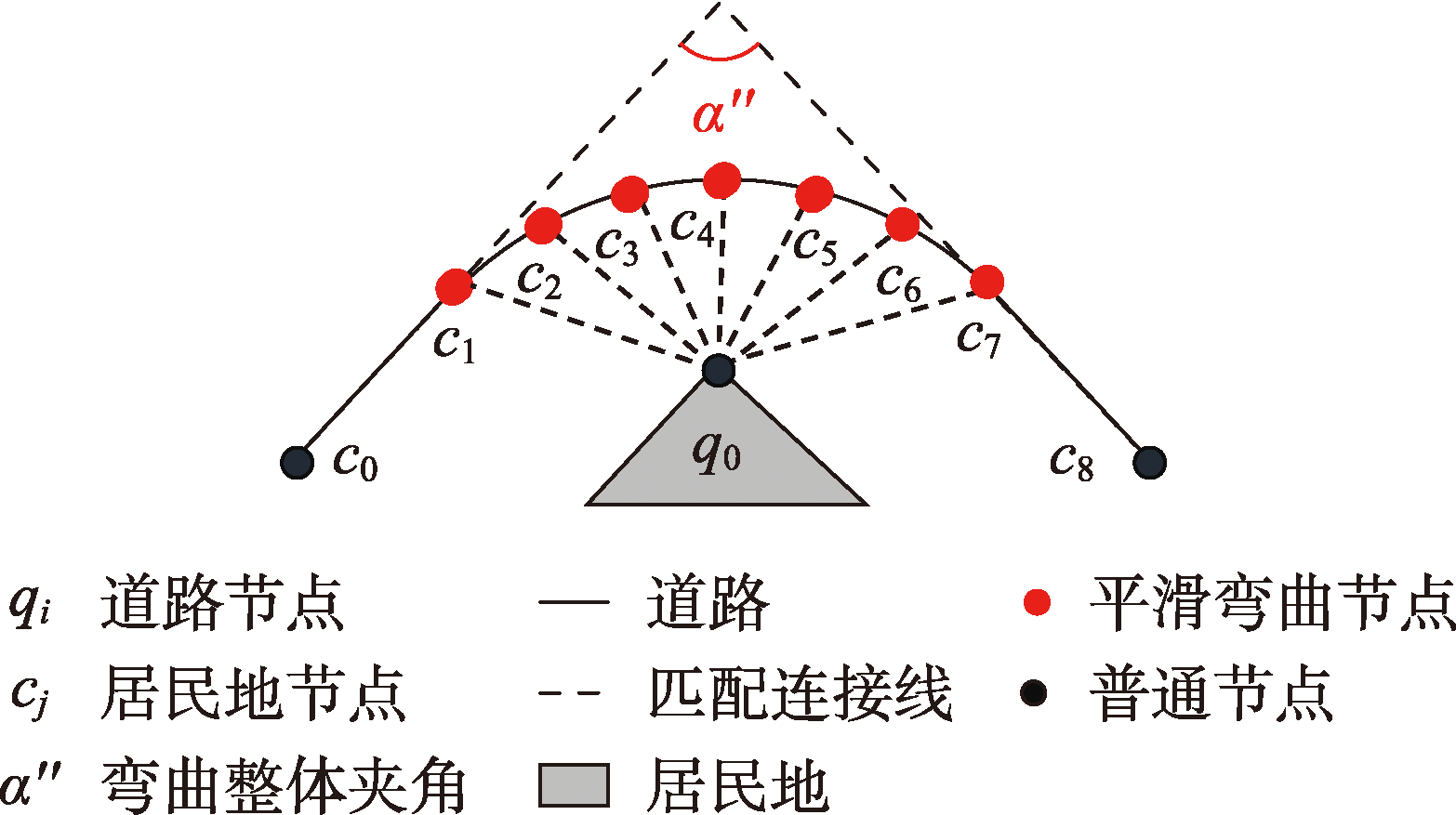
- 计算所有连接线的长度,剔除其中长度异常的连接线所对应的匹配关系。若仅剩一条连接线,按1:1优化策略执行;否则,执行步骤(2)。
- 计算若干个居民地节点共同构成的弯曲整体夹角α",α"为匹配点外侧线段c₀c₁与线段c₈c₇延伸线的交角。
- 计算每个匹配点的节点角度,搜索与道路节点q₀角度差最小且Δβ、Δβλ均满足要求的节点cₜ
- 对比cₜ及匹配点群与道路节点q₀的相似度,若cₜ与q₀更相似,则仅保留点cₜ的匹配关系,否则保留整个匹配点群的匹配关系。
3 实验与分析
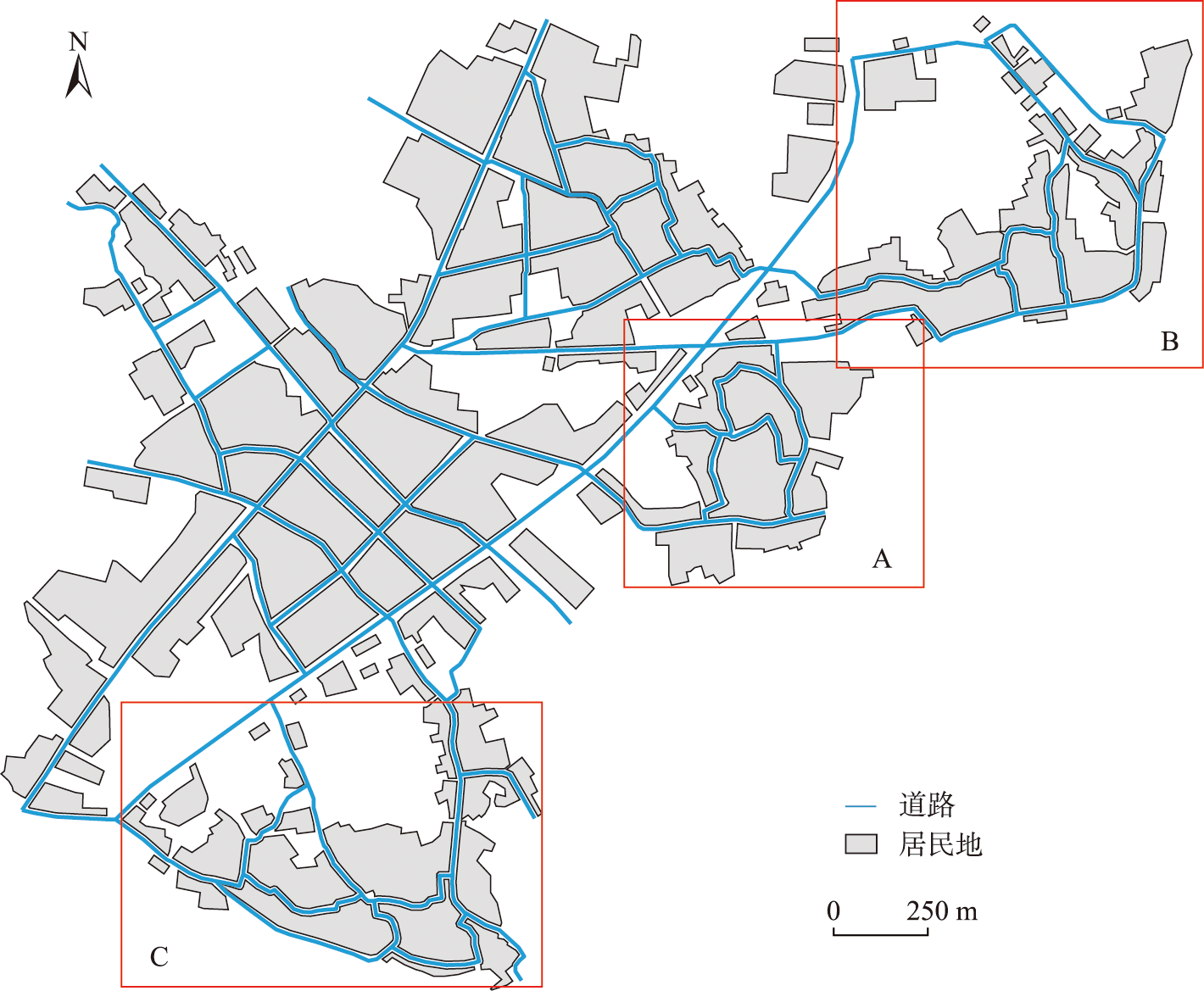
采用浙江省某地区1:5万地图的道路与居民地作为实验数据,包括114条道路及128个居民地,其中区域A、区域B及区域C的线状要素细节较丰富,如图10所示。
3.1 节点匹配分析
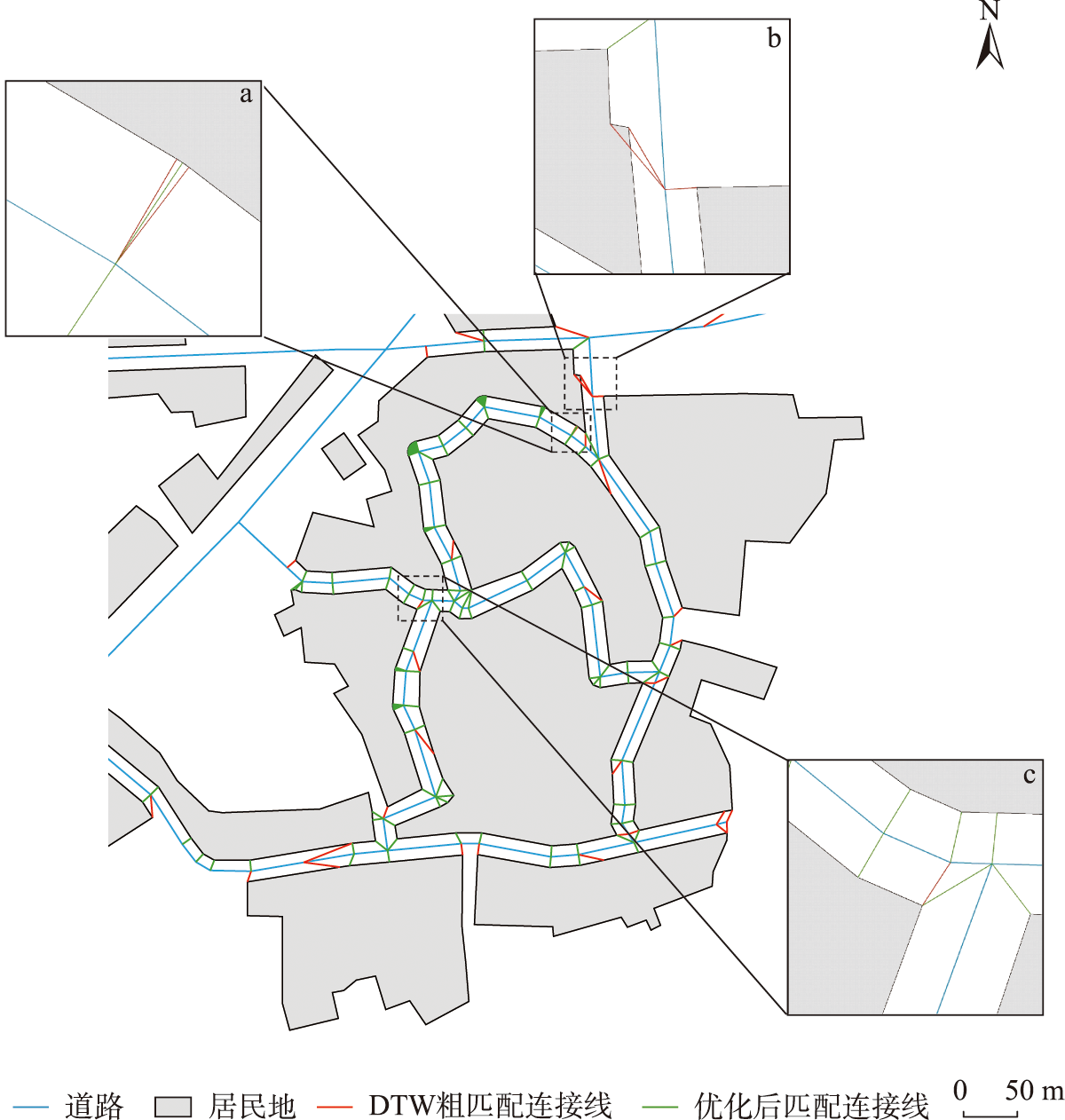
设毗邻距离pd为20m,节点角度差Δα的阈值v₁为20°,角平分线方向差Δβ的阈值v₂为90°,连接线与道路或居民地的节点角平分线的方向偏差Δβλ的阈值v₃为20°。以区域A为例,提取毗邻片段并进行节点匹配,匹配结果如图11所示。图11(a)中粗匹配结果存在一对多匹配,但中间的居民地节点足以与道路节点匹配,两侧连接线可删除。图11(b)中居民地轮廓上的2点与对应道路节点差异较大,删除2个居民地节点的连接线。图11(c)存在过匹配,目标居民地节点为直角拐点,仅与道路交叉口匹配,删除与另一个道路节点的连接线。DTW算法对道路与居民地在毗邻区域的所有节点按距离进行匹配,在此基础上做进一步优化,匹配结果较为精确,可用于协同化简。
3.2 与独立化简方法的对比
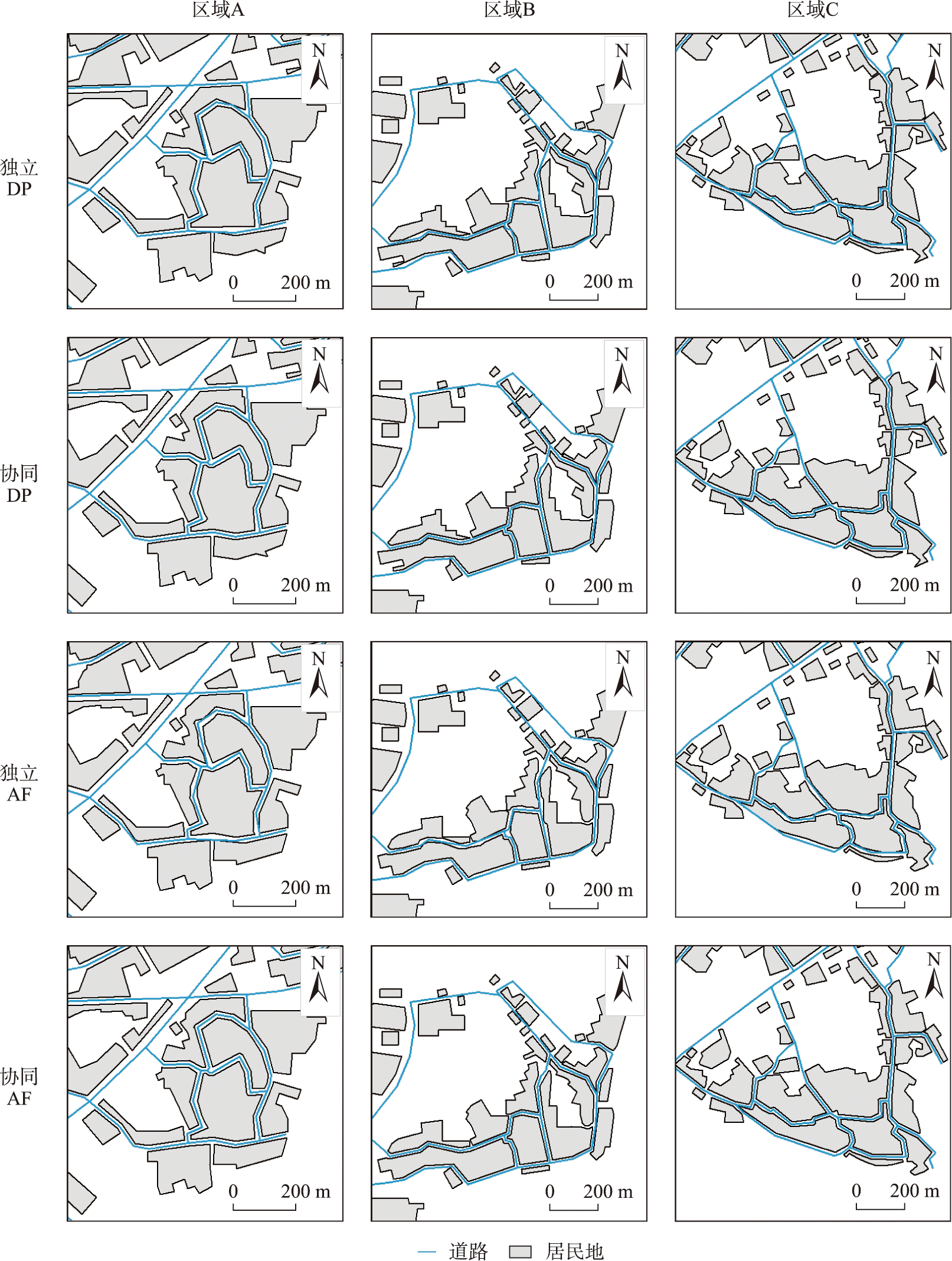
设化简阈值为10m,采用Douglas-Peucker算法(简称DP)对道路进行分段化简,对居民地节点做联动取舍后,分别采用Douglas-Peucker算法与邻近四点法(简称AF)对居民地轮廓进行分段化简,区域A、区域B及区域C的化简结果如图12所示。观察分析可知,独立化简的道路与居民地在毗邻区域普遍存在形状不一致的情况,原数据中的近似平行关系未有效保留,且存在较多拓扑错误。协同化简则较好地保持了道路与居民地在毗邻区域的形状相似性,道路与居民地间的近似平行关系显著。协同化简的居民地在毗邻区域的化简风格与道路相同,在非毗邻区域则能够体现自身化简算法的特点。
对化简结果做进一步的定量分析,采用式(2)所示的平行系数评价毗邻区域的形状相似性,结果如表1所示。平行系数是一条线要素中节点到另一条线要素的最小距离的波动程度,反映了线要素间的形状相似性,相似程度与值成反比。独立化简的平行系数大幅上升,说明道路与居民地在毗邻区域的形状相似性受到严重破坏,化简质量不佳。协同化简的平行系数值与原数据差异较小,表明协同化简方法能够较好地保持要素间的形状相似性。此外,协同DP算法的平行系数值略小于原数据,是因为部分与道路毗邻的居民地轮廓缺少可匹配的道路节点或形状与毗邻道路不相似,所以采用居民地自身的化简算法。DP算法减少了该部分轮廓的细节,提高了线的平直程度,进而增大了平行系数值。邻近四点法主要处理凹凸结构,对非凹凸结构的平直程度影响不大,所以其平行系数值略大于原数据。
式中:PCQ为片段C对片段Q的平行系数,反映C中节点到片段Q最小距离的波动情况,值越小,平行程度越高,反之越低;n为片段C中的点数;di为片段C中每个点到片段Q的最小距离;d̄C为片段C中点到片段Q最小距离的平均值。
4 结论与讨论
4.1 结论
道路与居民地是一对具有强空间相关性的地理要素,部分居民地在经过整体形态化简后以街区的形式存在,其轮廓与毗邻道路有着显著的形状相似性,为保持两种要素在毗邻区域的空间关系及协调视觉效果,提出了一种道路与居民地的协同化简方法。通过节点匹配建立道路与居民地在毗邻区域的节点级关联关系,将道路上的节点取舍同步至毗邻的居民地轮廓,实现协同化简。实验表明,本方法能够同步化简目标道路及其两侧毗邻居民地,化简后的道路与居民地在整体形态、局部细节等方面保持高度一致,空间距离相对均衡,道路两侧居民地的形状结构吻合良好。协同化简结果的视觉感受较为和谐,有效保持了道路与居民地在毗邻区域的形状相似性与拓扑一致性。此外,在非毗邻区域可为居民地轮廓灵活选择算法,根据实际情况呈现出不同化简风格。
4.2 不足与展望
本方法的不足主要在于:①只能同步节点的取舍,无法同步节点的位移,化简道路时只能选择基于节点取舍的化简算法;②存在包括移位冲突与符号化冲突在内的系统性拓扑冲突,属于算法原理层面的问题;③受节点匹配方法限制,本方法适用于图形结构较为规整的道路、居民地等人工地理要素,难以处理湖泊、河流等更为复杂的自然线面要素,且化简算法、匹配结果优化中的参量需要结合数据实际情况进行多次尝试以确定合适的阈值。
下一步将研究兼顾节点增减、移位的协同化简方法,扩大化简算法的选择范围,优化节点匹配方法,增强其对复杂场景的应对能力,并进一步协同道路化简与居民地移位、压缩等算子。