研究背景
PM2.5的健康影响
PM2.5作为空气污染物的主要成分之一,严重影响人类身体健康,如呼吸系统受损、癌症与心血管疾病的发病率增加等。如何降低人类在PM2.5中暴露程度是当下可持续城市和社会发展的重中之重。
预测技术现状
目前已有PM2.5浓度预测模型过多专注于提升模型预测精度,但忽略了模型的可解释性,造成模型可复用性和可信任度较差。大多数时空预测模型却难以兼顾预测精度及可解释之间的均衡。
模型概述
注意力时空常微分方程(ASTODE)模型
本文提出了一种新颖的兼顾预测精度和可解释性的PM2.5浓度预测模型,即注意力时空常微分方程(Attentional SpatioTemporal Ordinary Differential Equation, ASTODE)。
时空常微分方程模块
通过设计了一种新颖时空导数网络将传统NODE扩展到了时空常微分方程,进而挖掘PM2.5浓度数据中的时空关系。
时空注意力模块
构建了一种可解释的数据结构(即注意力机制)辅助时空常微分方程捕捉PM2.5浓度数据中的长期依赖关系。
图1 ASTODE模型的整体示意
核心组件
时空常微分方程模块
传统NODE虽具备一定的可解释性,但仍存在不足:
- 传统NODE的导数网络仅依赖时间因素,没有考虑多监测站点的情形
- 传统NODE在求解过程中仅依赖初值,使该模型难以挖掘PM2.5数据中长期依赖关系
本文提出了时空导数网络将传统NODE扩展到了时空常微分方程。时空导数网络数学定义如式(3)所示:
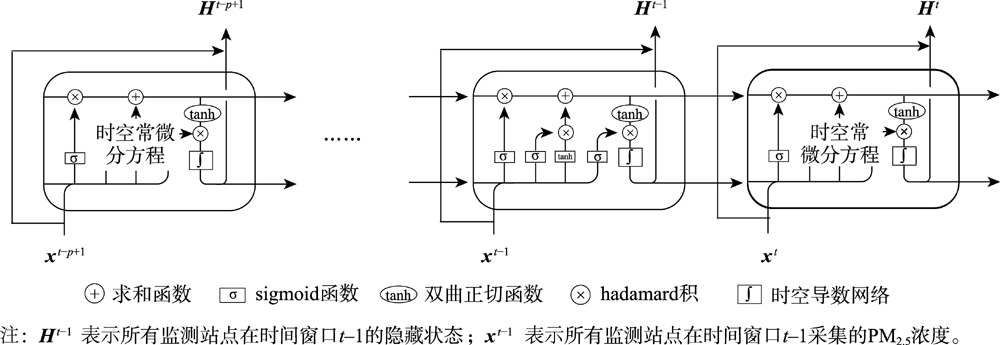
图2 时空常微分方程模块的前向传播过程
时空注意力模块
时空注意力模块由空间注意力和时间注意力组成:
- 空间注意力用于在空间维度融合n个监测站点的隐藏状态
- 时间注意力用于在时间维度融合p个时间戳的隐藏状态
注意力机制是一种可解释的数据结构。以空间维度的注意力机制为例,注意力机制可视为反距离权重函数在数据驱动下的一种扩展。
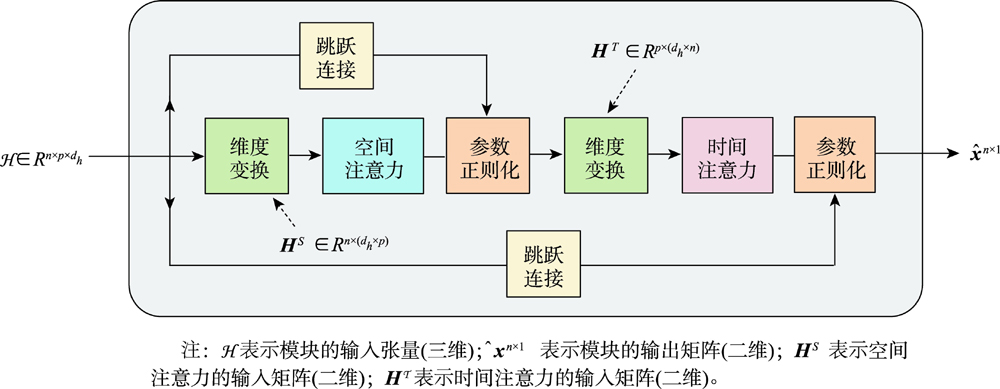
图3 时空注意力模块的前向传播过程
实验与分析
实验数据
本研究采用的PM2.5浓度数据集来源于天津市的27个空气质量监测站点,时间跨度为2015年2月1日—2015年4月30日,采样间隔为60min。
预测结果分析
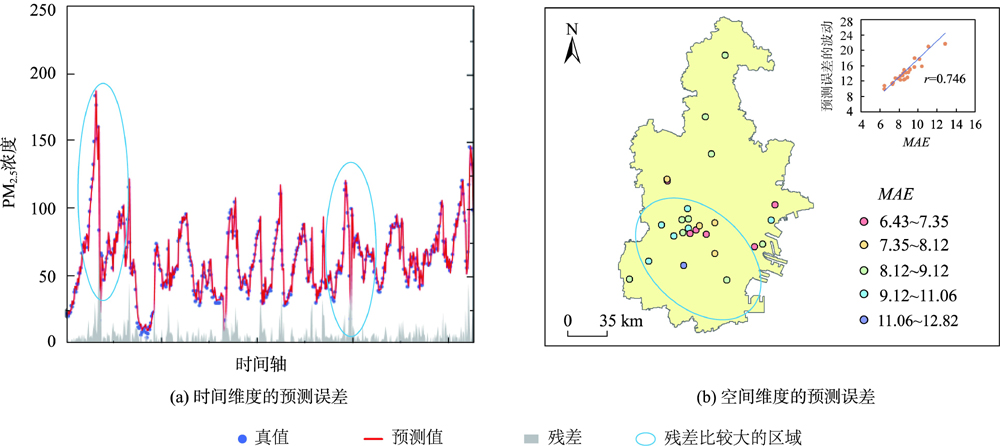
图4 ASTODE模型的定性预测结果
图7从时间维度和空间维度定性描述了ASTODE模型的预测性能:
- 时间维度:大多数时刻观测真值与模型预测值的残差较小,少量时刻观测真值与模型预测值的残差较大(蓝色区域)
- 空间维度:大多数监测站点观测真值与模型预测值的残差较小,少量监测站点观测真值与模型预测值的残差较大(蓝色区域)
基准方法对比
| 模型 | MAE | RMSE | MAPE/% |
|---|---|---|---|
| ST-KNN | 14.35 | 22.12 | 32.02 |
| T-GCN | 10.20 | 17.97 | 25.14 |
| BTMF | 8.98 | 15.42 | 20.74 |
| GDGCN | 8.56 | 15.11 | 19.47 |
| Vanilla-NODE | 13.34 | 19.52 | 35.06 |
| ODE-RNNs | 9.67 | 15.99 | 23.22 |
| ASTODE | 8.63 | 15.14 | 19.54 |
实验结果表明,ASTODE模型解决了传统NODE的两点不足,兼顾模型可解释的同时,优于或者逼近于现有基线方法的预测精度。尤其是ASTODE模型已经逼近于GDGCN模型的预测精度,这证明了在不考虑模型可解释性的情况下,ASTODE模型已经具备了令人可接受的预测结果。
模型可解释性分析
本研究从2个方面解释ASTODE模型:
- 解释时空常微分方程模块学习到的导数值:10:45之前和19:45之后是PM2.5上升的主要时间段,10:45分—19:45是PM2.5下降的主要时间段,这恰好与可视化的导数值相对应。
- 解释时空注意力模块学习到时空关系:在时间维度,t时刻的预测值受到历史3个时刻的影响;在空间维度,邻域监测站点对目标监测站点的影响权重存在明显差异。
结论与展望
研究结论
可解释的准确预测PM2.5浓度变化对人类健康风险评估和政策实施具有重要意义。本文提出的ASTODE模型:
- 将神经常微分方程集成到时空预测任务中,提升模型可解释性
- 提出时空导数网络和时空注意力机制提升模型捕捉时空关系的能力
- 实验表明ASTODE模型在预测精度上优于或等于存在的先进基线方法
未来工作
本研究的局限性:
- ASTODE模型基于ODE完成时空预测任务,训练过程耗时
- 仅验证了ASTODE模型的单步预测性能,未验证多步预测能力
下一步工作重点:
- 优化ASTODE模型的前向迭代和反向传播过程,提升训练效率
- 验证ASTODE模型多步预测能力