1. 引言
离群点探测是数据挖掘的一个重要研究领域,其目的是通过数据挖掘方法发现离群点中潜在且有意义的重要知识与规律,可应用于城市气候观测、环境监测、犯罪行为检测和医学异常检测等方面。
POI离群点探测角度
空间分布差异
概括程度较低的点通常泛在地、集聚地分布于道路两旁,大多为非离群点,而占地面积较大的地理实体(如校园、住宅区、机场等)POI概括程度高,常采用分布稀疏的少量点表示。
空间上下文差异
各类型POI的空间依赖性不同,一些频繁出现在同一地点的实例类型组合构成了全局或局部的流行同位模式,而未构成同位模式的点由于存在空间上下文特征的差异,一定程度上可判定为离群点。
时空关联性因素
由于特殊事件触发、城市人群行为变化、文化活动等时空关联性因素影响,导致在特定区域内一些POI实例及其周围点的使用频率发生变化,因此形成离群。
本文重点讨论角度①下的离群点探测问题。现有POI离群探测方法面临挑战:它们无法充分表达和量化POIs的局部空间分布特征,且这些方法的有效性需要进一步研究。
2. 基于局部集聚特征尺度判定的兴趣点离群分布探测方法
POI离群分布的本质源于其对地理实体的概括表达,由于地理数据固有的空间异质性及不同抽象程度,导致POI在不同空间尺度上表现出集聚程度差异,形成了全局离群及局部离群等模式。
本文方法基于两个算法模块:POI局部集聚尺度判别方法和POI离群点探测方法。
2.1 兴趣点局部集聚尺度判别方法
POI的互邻近距离自某一尺度开始突然变大且点群呈不均匀分布,这是由于局部空间存在离群点导致分布疏密程度显著变化。
算法1:兴趣点局部集聚尺度判别方法
输入: 实例点集合Pnts
输出: 集聚特征尺度参数K
步骤:
1. 通过Delaunay三角化,粗略表达实例点集的空间邻近关系
2. 提取tri中的边集E,构建边集字典EdgeDic
3. 基于EdgeDic构建图结构,构建邻接链表EdgeLink
4. for k in [1,Max_K-1]:
5. 在EdgeLink中查找每个点的第K个及第K+1个节点
6. 计算交叉K与交叉K+1近邻距离方差比Ik
7. 若Ik < 1,继续执行for循环
8. 若Ik > 1,跳出循环,return K, EdgeDic
9. end for
2.2 POI离群点探测方法
通过算法1获得POI的局部集聚尺度参数K后,在该尺度下以每个点的K邻域截取Delaunay三角网,生成新的边集(TIN_part);在新边集上通过边长约束指标进行离群点探测。
定义3:边长约束指标
CI(Ei) = Mean(TIN_part) + α × STD(TIN_part)
α = Mean(TIN_part) / len(Ei)
式中:Ei和len(Ei)分别表示Delaunay三角网中任一边及其边长;Mean(TIN_part)和STD(TIN_part)为新边集的平均边长及边长标准差;α为适应系数。
算法2:POI离群点探测方法
输入: 局部集聚尺度参数K, 边集字典EdgeDic, 实例点集合Pnts
输出: 离群点探测结果Outliers
步骤:
1. 根据EdgeDic及K值,截取每个节点的K邻域,生成K_EdgeDic
2. for edge, edge_Length in K_EdgeDic:
3. 计算边长约束指标CI
4. if edge_Length < CI: continue
5. else: 删除edge相关的边记录
<6. end for
7. 将点集Pnts与K_EdgeDic中剩余节点作差集运算,获得初步离群点
8. 创建一个空列表,用于存储连接子图的直径
9. for sub_g in connected components of K_EdgeDic:
10. if len(sub_g.nodes) < K+1: 存储子图直径
11. end for
12. 计算直径数值序列的均值、中位数和标准差
13. 遍历所有子图,根据公式计算指标,若子图直径小于该指标则存入离群簇
14. 汇总离群点探测结果
15. return Outliers
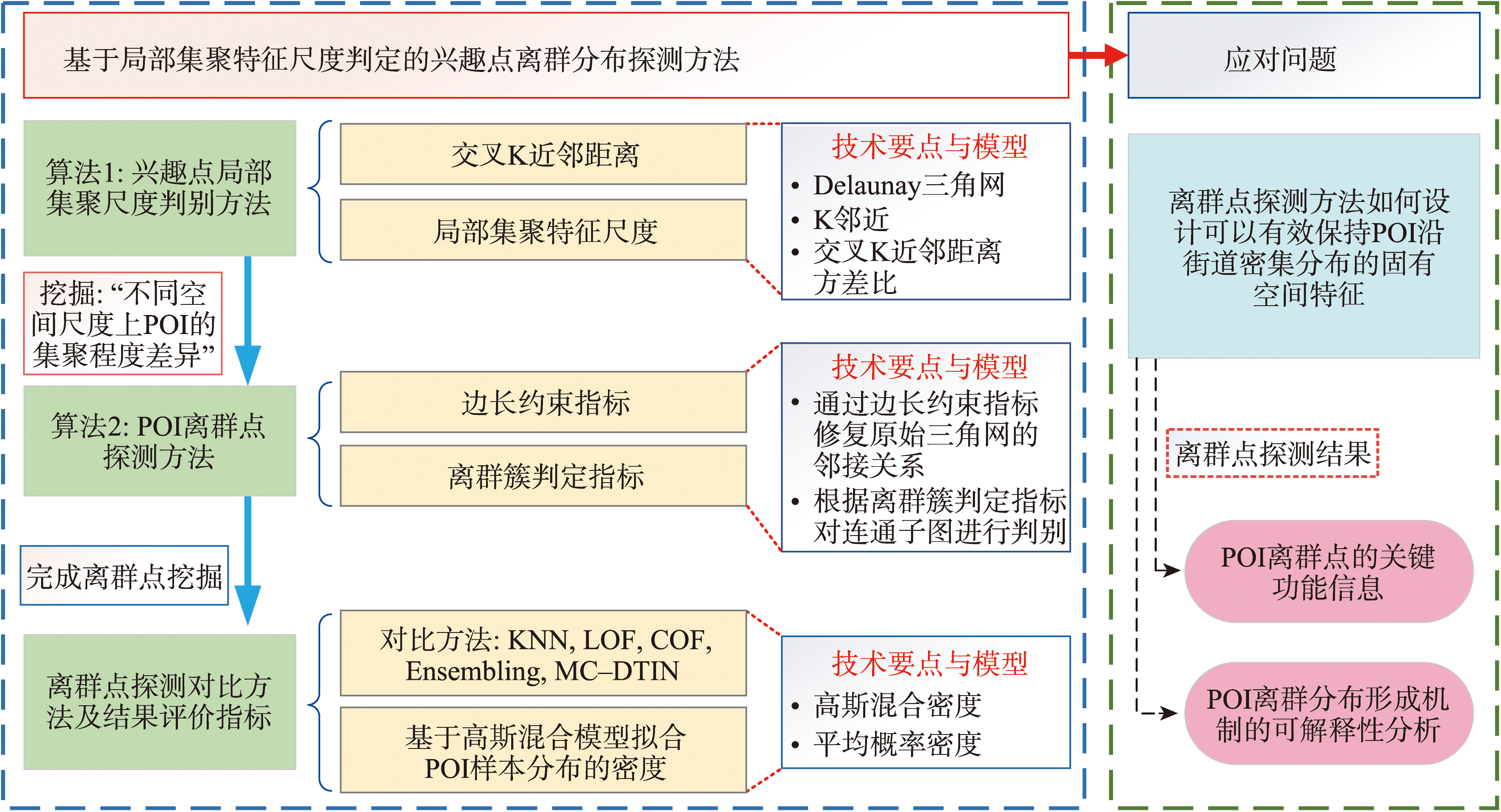
图1 本文方法基本框架
2.3 离群点探测对比方法及结果评价指标
本文基于PyOD库及层次约束TIN算法(MC-DTIN)搭建对比方法原型。选择MC-DTIN算法、KNN算法、LOF算法、COF算法及后三者的集成方法(Ensembling)作为对比方法。
表1 各离群点探测方法详细信息
| 算法名称 | 算法复杂度 | 算法描述 |
|---|---|---|
| KNN | O(N²logN) | 计算每个点与其他点的距离,并选择最近的K个邻居 |
| LOF | O(N²logN) | 通过比较每个点与其邻域点的密度,计算局部离群因子 |
| COF | O(N³) | 基于LOF,考虑全局信息,计算局部离群因子的平均值 |
| Ensembling | O(NlogN)+O(NlogN)+O(N³) | 构建共现矩阵(相似度图);计算拉普拉斯矩阵;特征值分解 |
| MC-DTIN | O(NlogN)+O(M)+O(N*m) | 构建Delaunay三角网;分别基于三层边长约束指标提取离群点 |
| 本文方法 | O(NlogN)+O(KN)+O(Nₚ)+O(Nₛᵤb_g(K+1+E)log(K+1)) | 构建Delaunay三角网;识别显著局部集聚尺度并生成新边集;根据边长约束指标提取离群点,并在剩余点集中识别离群簇 |
由于POI数据本身缺乏分布模式是否离群的先验知识,本文基于高斯混合模型(Gaussian Mixture Model, GMM)拟合POI样本分布的概率密度函数,构建各点与概率密度的映射关系,通过结果观察及指标分析两个方面进行所选方法的有效性评价。
3. 实验及结果分析
3.1 实验数据
本节通过小样本POI数据开展对比试验分析,以检验本文方法的有效性,数据采集于百度地图API。实验原型基于Python3.8开发,在64位WIN7环境中部署并测试。
表2 各城市POI样本数据信息及其在本文方法中的离群点探测结果
| 城市 | 点要素数/个 | 路网类型 | 集聚特征尺度 | 离群点数/个 |
|---|---|---|---|---|
| 北京 | 21928 | 棋盘状 | K=3 | 1487 |
| 上海 | 2992 | 蛛网状 | K=3 | 167 |
| 西安 | 12235 | 棋盘状 | K=3 | 764 |
| 成都 | 10269 | 环形放射状 | K=2 | 1165 |
| 长春 | 9461 | 放射状 | K=2 | 855 |
| 包头 | 33101 | 环形放射状 | K=2 | 2687 |
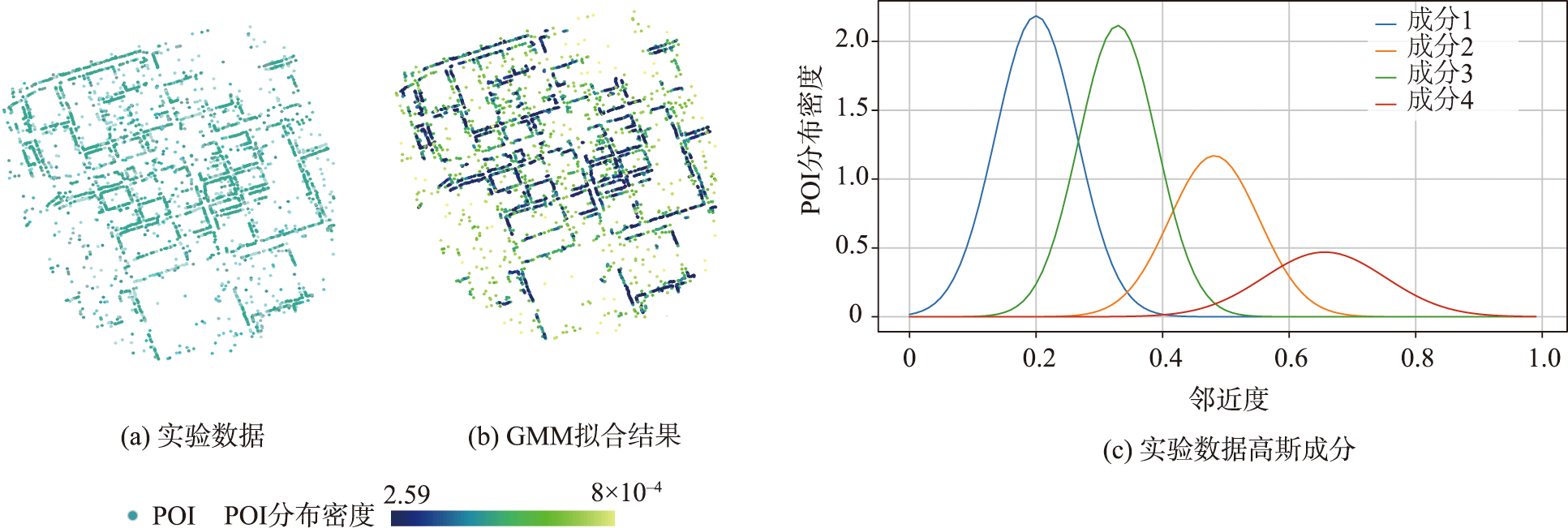
图2 实验数据及GMM拟合结果
3.2 POI试验结果与分析
POI具有泛在地、密集地分布于街道空间的固有特征,并多呈"线型"分布的非凸形状簇。本文重点讨论由于POI空间分布差异导致的离群现象,结合其固有分布特征可大致推断:POI的非离群点可能更多地分布于街道空间,而离群点则会在剩余空间中随机、松散地分布。
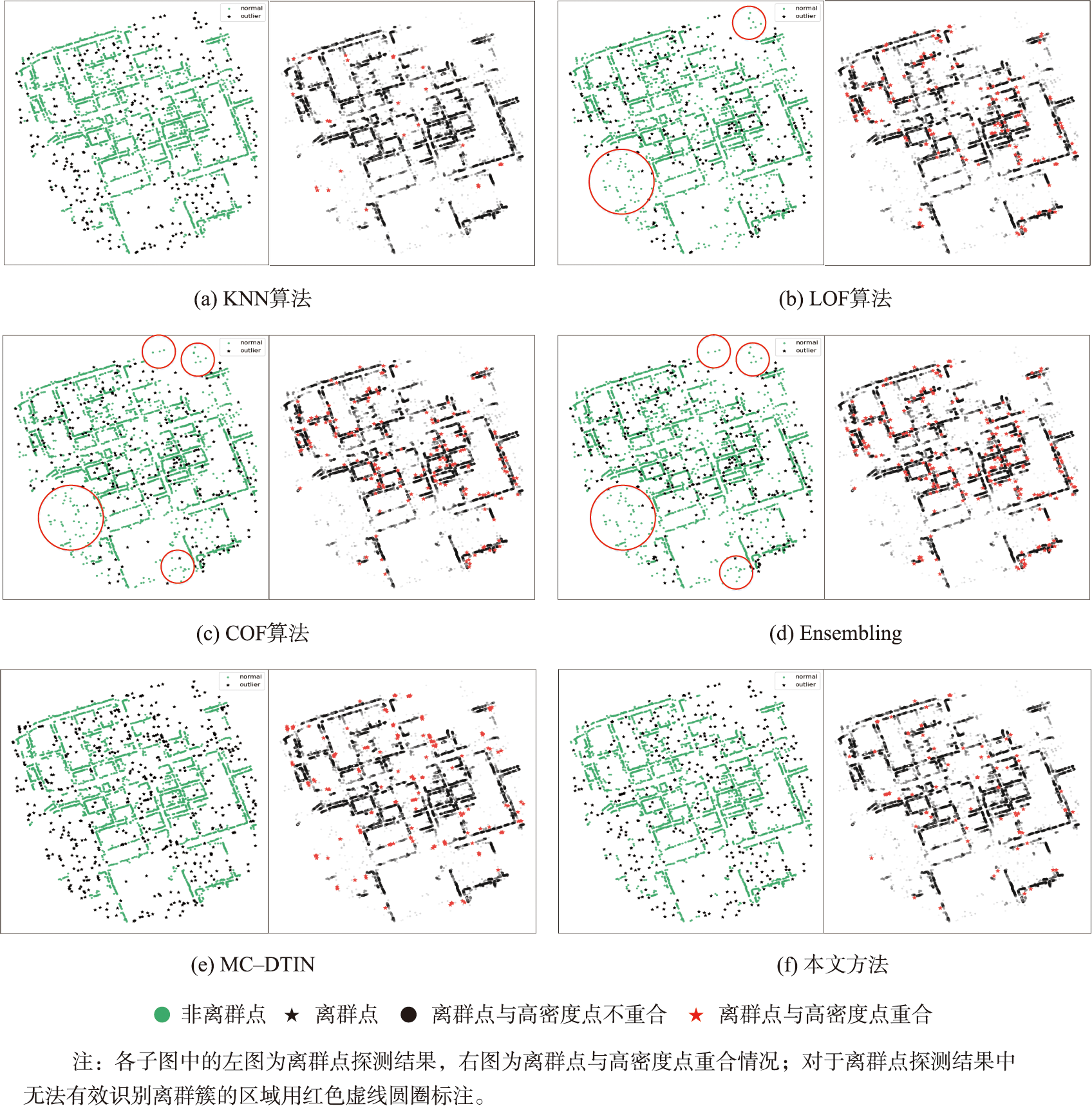
图3 POI离群点探测结果
从离群点与高密度点重合情况来看,本文方法、KNN及MC-DTIN算法结果中重合点较少,并且对POI街道空间分布特征保持良好;LOF、COF及Ensembling算法结果中重合点较多,并且大量重合点存在于街道空间,较少顾及POI街道方向上的集聚性。
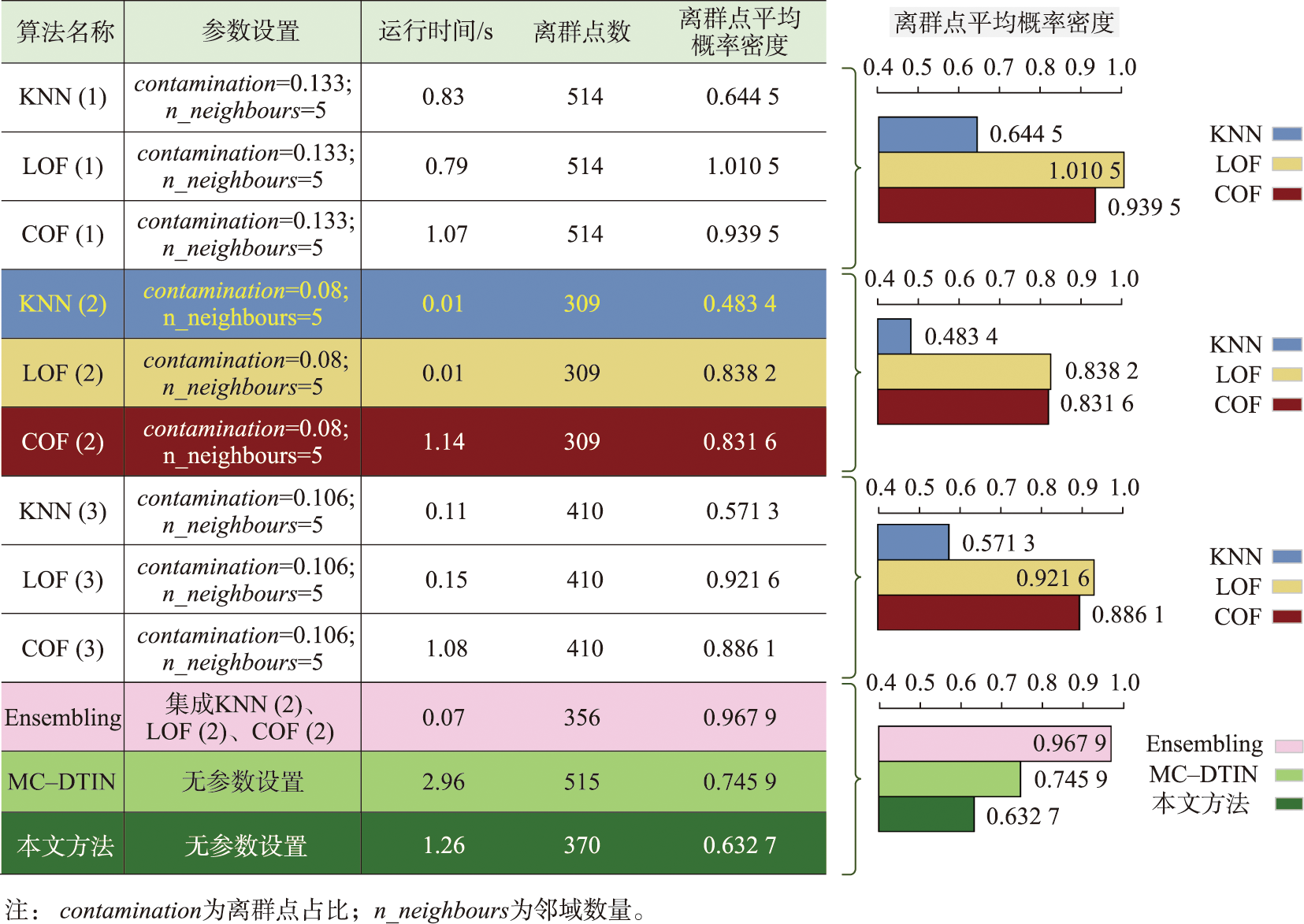
图4 POI数据试验的参数设置、离群点平均概率密度及运行时间统计
图7为各方法的详细配置信息及相关指标测试结果。由于离群点平均概率密度越低,则说明该方法所获得的离群点中较少混杂非离群点。基于该指标可说明本文方法、KNN及MC-DTIN算法的离群探测结果相较于其他3个方法更为有效。
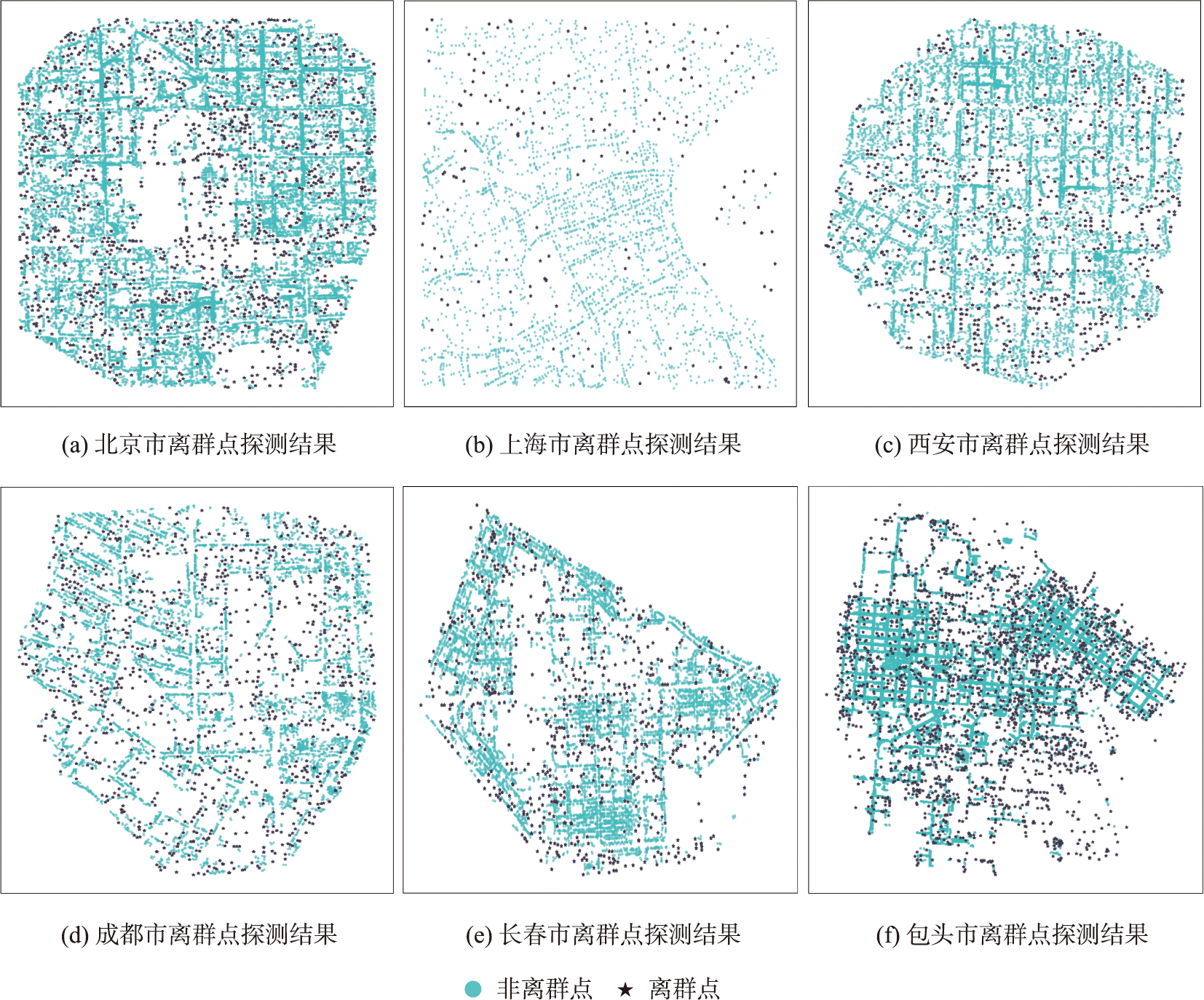
图5 本文方法普适性验证
为进一步验证本文方法普适性,以城市路网结构(棋盘状、环形放射状、蛛网状)及城市发展规模为参考,遴选并截取北京市、上海市、西安市、成都市、长春市及包头市的部分区域POI数据参与验证。可以观察得出,对于不同路网结构约束下的POI要素,本文方法仍可以在顾及POI街道空间分布特征的前提下有效探测离群点,方法具备普适性。
4. POI离群探测结果的可解释性分析
讨论离群点的产生原因并给予解释说明是离群探测的主要任务之一,兴趣点离群原因涉及城市规划变化、人群行为及社会活动等方面。本文基于本文方法对北京市中心城区内249535个POI进行离群点探测,共探测POI离群点23359个。
4.1 POI各类型离群点数量占比及其空间分布特征
本小节通过离群点类型占比以及Ripley's K函数分析方法对离群点探测结果进行解释,挖掘POI数据中离群点的潜在分布模式。
高离群点占比的POI类型主要来源3个方面:①具备特殊的业务或活动,如高尔夫球场、大型露营公园、市政府、宗教场所等;②大型的自然或人工景观带,如农场果园、滑雪场、海洋馆、动植物园等;③满足社会需求的特殊专项服务设施,如机场、火车站、交通服务设施(桥、油/气供给站、出入口等)、殡葬服务等。
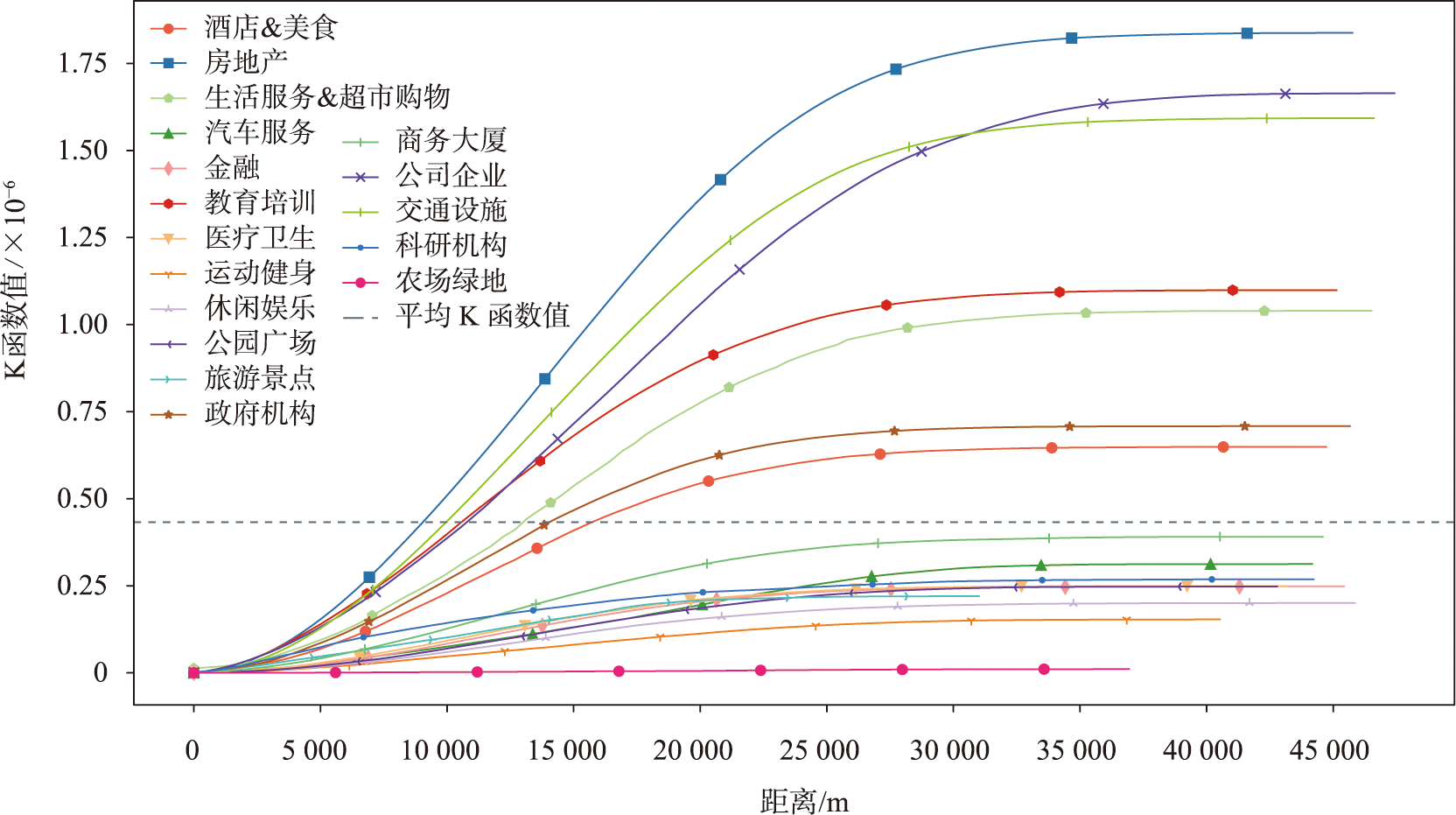
图6 基于Ripley's K函数的离群点分布分析
通过观察各类型离群点的Ripley's K函数曲线可以得出:房地产、公司企业、交通设施、教育培训及生活服务类要素在20000-25000m范围内呈现集聚分布;其他类型的函数曲线增长趋势相对平缓,说明这些类型的离群点在全局范围内呈随机分布。
4.2 离群POI的面积占比及其公众认知水平分析
POI通常标注在地理实体的中心点或实体范围内的其他代表性点上,将大范围区域抽象为一个点也是POI离群的可能原因之一。本文选用北京市AOI数据与POI离群点进行匹配,对POI离群成因作进一步分析。
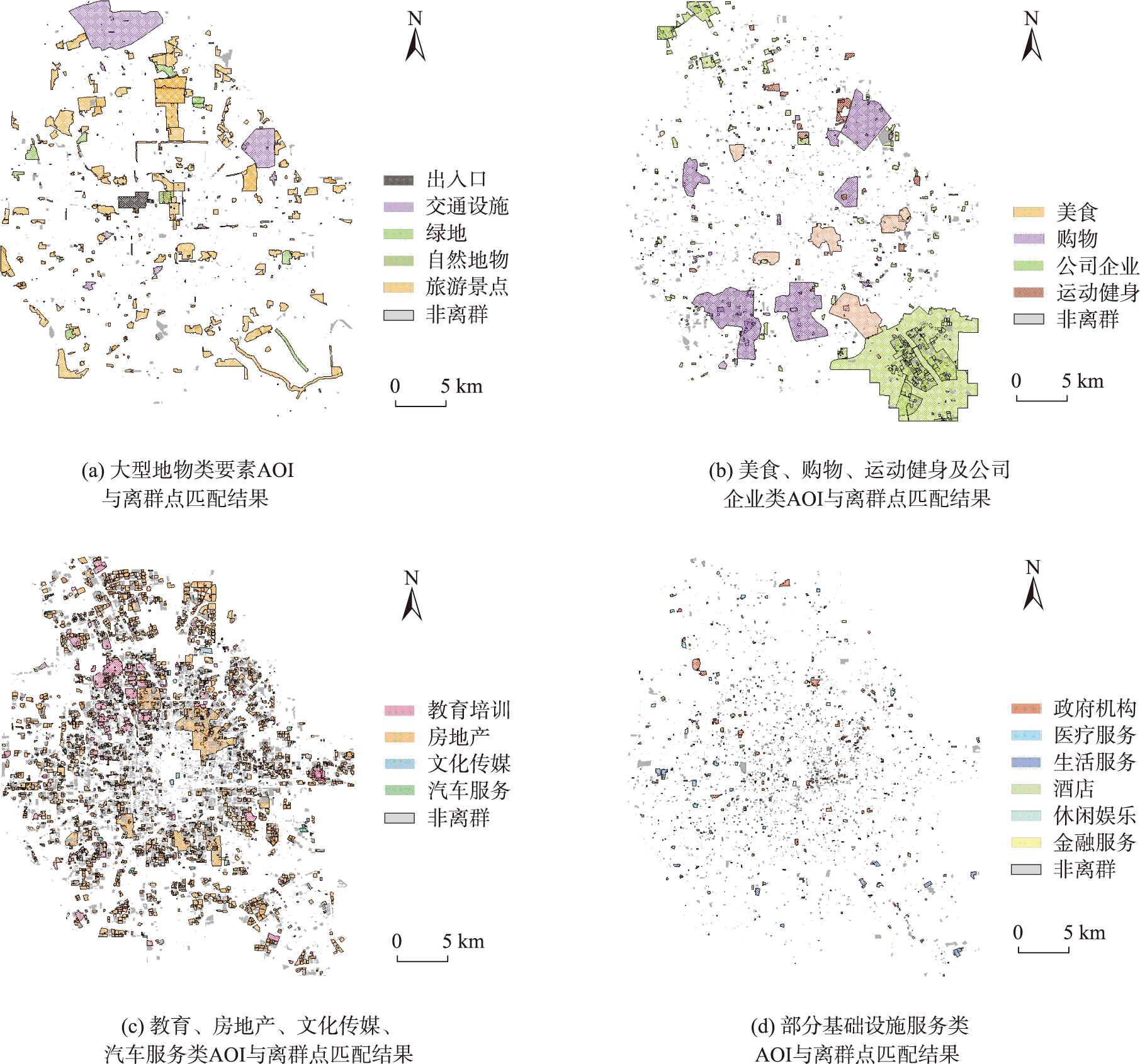
图7 离群点与AOI匹配结果
通过统计分析各类离群AOI要素的面积占比可知:①大型地物类离群要素有较高的面积占比,如出入口类(99.96%)、自然地物类(98.81%)、绿地类(97.87%)等;②美食类、购物类、公司企业类、运动健身类AOI与离群点也呈现大量匹配;③离群要素面积占比在60%以上的AOI类型还包括房地产类(63.15%)、教育培训类(67.95%)等。
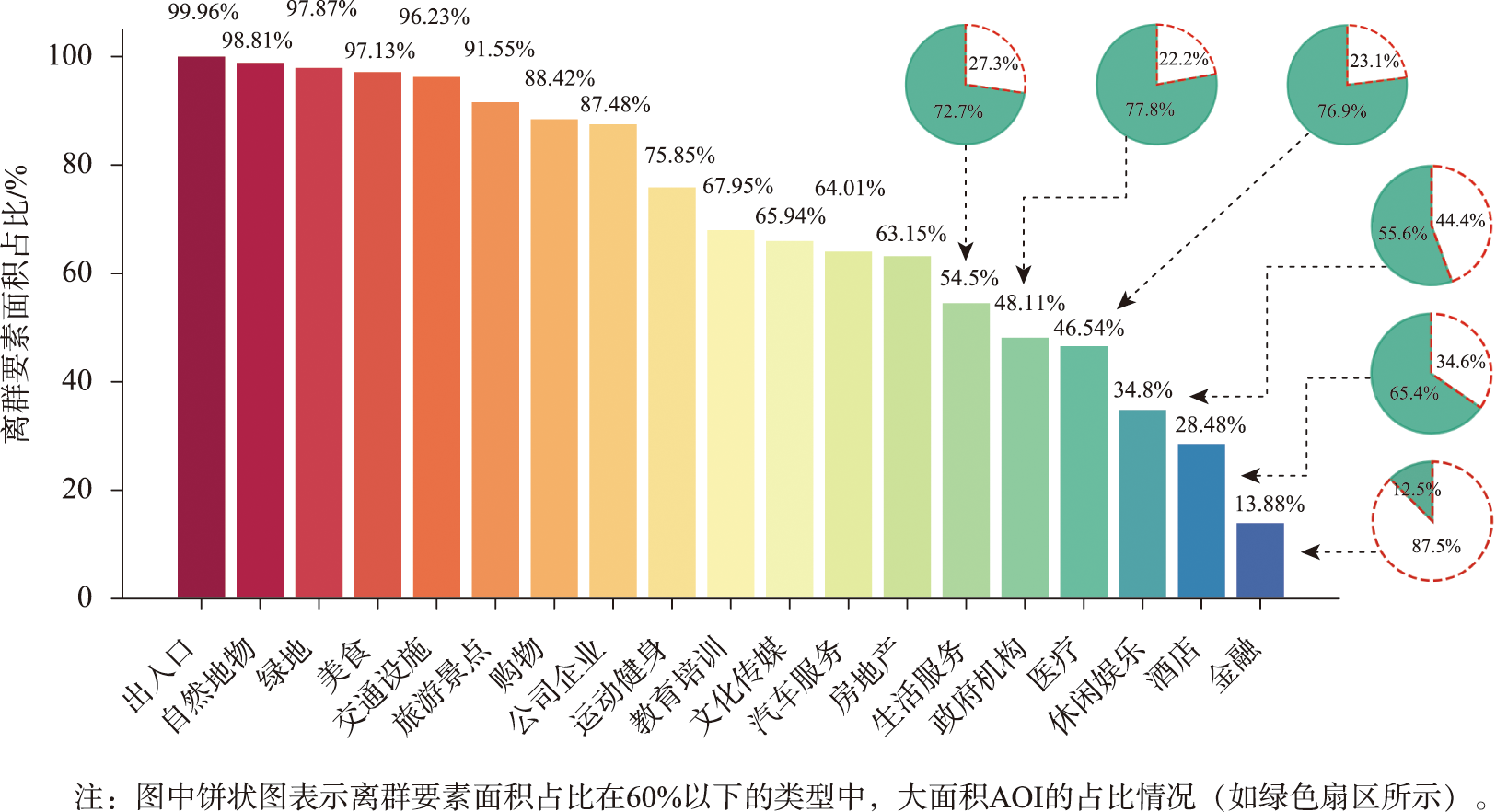
图8 离群AOI要素的面积占比分析
最后,本文以AOI的大众评分来量化各类型离群点的公众认知水平。从箱体长度来看,公司企业类、金融类、生活服务类、文化传媒及政府机构类箱体长度较长;从中位数位置来看,酒店、旅游景点、文化传媒及自然地物类型的离群点认知水平分布集中且均具有较高的公众认知度。
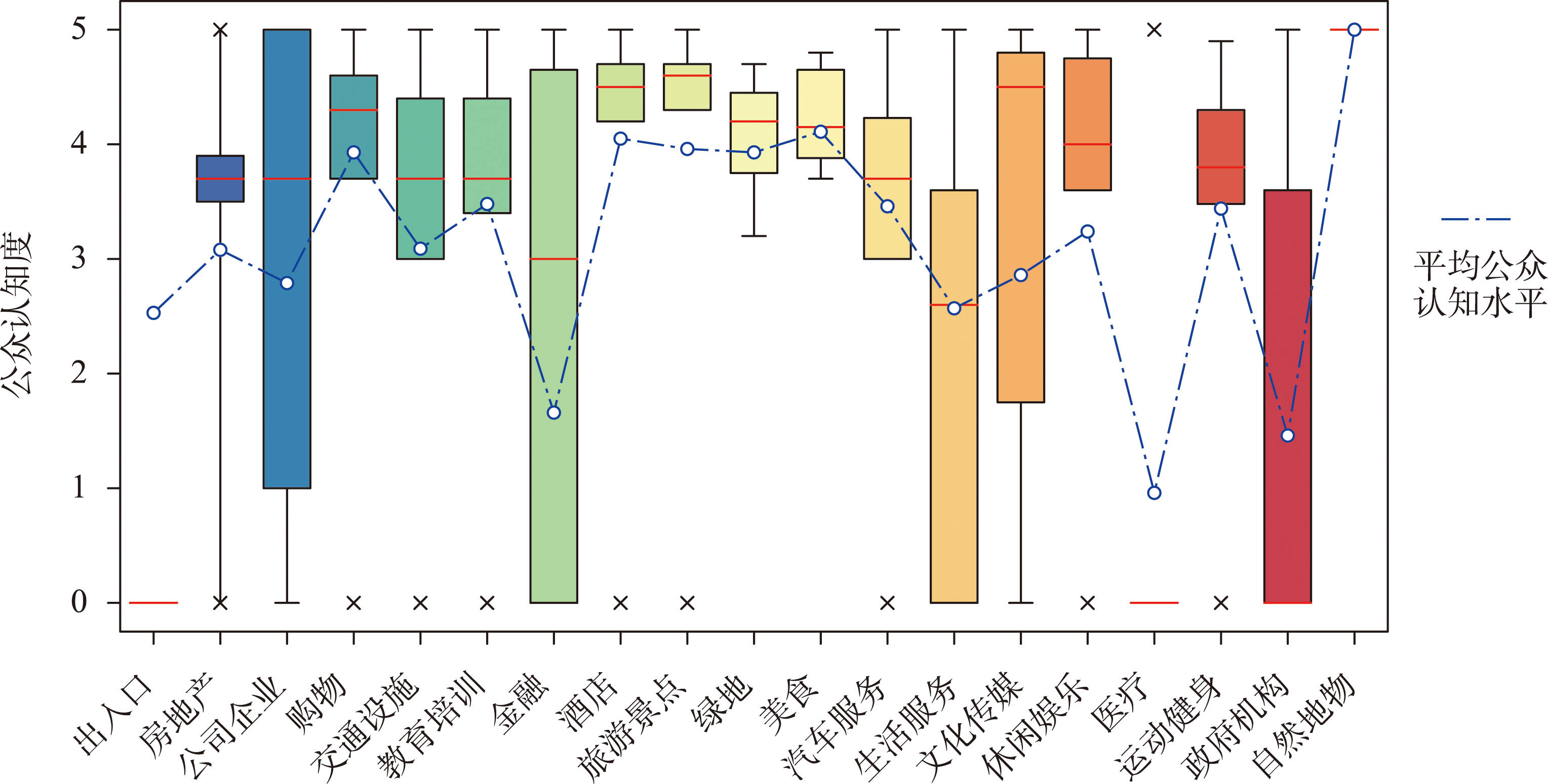
图9 离群点的公众认知水平
综上所述,本文通过构建POI离群点与类型占比、空间分布、占地面积及公众认知度的关联,实现POI离群分布的可解释性分析。分析结果说明当POI要素具备自身功能独特性、大面积占地范围、高抽象程度及知名度时,或在这几个因素综合影响下,较易形成离群分布格局。
5. 结论与讨论
POI离群点探测已广泛应用于多源数据匹配、城市要素范围划定等领域,但现有离群探测方法对POI空间分布固有特征缺乏考虑,且相关研究成果中对POI离群点缺乏进一步应用及解释分析。
本文着眼于因POI空间分布差异导致的离群现象,提出基于局部集聚尺度判定的兴趣点离群分布探测方法。该方法通过Delaunay三角网及交叉K近邻距离表达点群的邻近关系,并围绕图边长及子图直径构建约束指标,在顾及POI局部分布特征的前提下获得离群点。
通过与最优参数配置下的KNN、LOF、COF、Ensembling算法及无参数的MC-DTIN算法进行比较,可得出本文方法具备以下优势:
- 相较于局部离群因子测算类算法及Ensembling算法,本文方法继承了KNN算法在任意点局部密度表达上的优势,离群探测结果与高密度组分的非离群点鲜有重合,较好顾及POI在街道方向的集聚性
- 无需通过预实验获得适配参数,减少算法前期开销,并且相较于同为无参数方法的MC-DTIN算法,本文方法通过尺度参数递增的方式寻找局部邻近关系突变,有效避免微小离群簇对POI原分布结构的干扰
- 本文方法普适于不同发展规模城市及各类路网结构约束下的POI要素
利用本文方法对北京市POI数据进行离群探测,并从空间分布特征、类型数量、面积占比以及公众认知水平等方面对离群点开展可解释性分析,合理揭示了兴趣点在现状规划背景下的离群分布成因。
未来研究方向
空间依赖性分析
结合各类型POI不同的空间依赖性探测并解释其离群现象
时空关联性研究
根据时空关联性因素开展POI在特定情境下的离群探测及变化分析
基于该方法的相关研究可辅助城市规划与决策者更全面地把握城市发展动向,并为资源配置优化、提高城市可持续性及人居生活质量等方面提供新的方法及研究视角。
* 以上内容由AI自动生成,内容仅供参考。对于因使用本网站以上内容产生的相关后果,本网站不承担任何商业和法律责任。