摘要
时空数据的缺失和稀疏分布是普遍存在的现象,时空插值是解决数据缺失和稀疏分布的重要手段。现有的时空插值方法大多未同时考虑数据的长期时间相关性以及全局空间信息。
本文结合长短时记忆网络LSTM与数据的空间特性构建了时空插值模型:
- 模型利用空间层剔除弱相关性的信息,提取相关性更强的空间信息输入LSTM网络;
- 由于传统人工神经网络ANN模型无法考虑时间对插值的影响以及单向LSTM模型仅能考虑过去时刻对当前时刻的影响而不能利用未来时刻的信息,本文使用双向LSTM模型BiLSTM体现时间相关性;
- 为了有效提取全局空间特征并保留BiLSTM双向建模的优势,本文将自注意力机制引入BiLSTM中,构建了融合自注意力的双向LSTM插值模型SL-BiLSTM-SA。
在实验设计阶段,模型被应用于山东省PM2.5浓度数据集进行插值效果研究,并与其它模型进行性能比较。实验表明,SL-BiLSTM-SA模型有着更低的误差度量,相较时空普通克里金STOK和遗传算法优化的时空克里金GA-STK精度分别提高了39.83%、36.63%,且能较准确地预测高值和低值。
关键词:
1 引言
时空数据的缺失和稀疏分布是普遍存在的现象,时空插值是解决数据缺失和稀疏分布的重要手段,时空插值通过捕获时空依赖关系,利用已知位置和时间上的观测值来推断未知位置和时间上的变量值,换言之,时空插值方法可估计地理现象随时间的几何和属性数据变化。
随着地理分析技术的发展,目前时空插值方法主要基于统计学、机器学习和深度学习建模时间和空间因素,揭示时空数据的演变过程和时空分布规律。
基于统计学的插值模型往往具有明确的数学描述,如经典的反距离加权IDW和克里金,其中,时空克里金利用变异函数模型表征随机变量的变异结构或时空连续性,描述变量的时空结构特征。
机器学习和深度学习模型可以更准确地捕捉时空变量之间的非线性关系,因此越来越多地应用于时空插值。然而,这些方法存在两方面局限:
- 地统计方法,如克里金插值,使用预先设定的线性/非线性方程来定义复杂的时空关系;
- 基于机器学习或深度学习的插值方法大多考虑了时空数据的短期相关性或局部空间特征,未同时考虑长期时间相关性和全局空间特征。
针对上述局限,本文融合空间信息,结合BiLSTM和Self-attention构建了时空插值模型,扩展了时空数据的插值手段,为时空数据分析提供了一定的理论和方法支撑。
2 研究方法
为了捕捉具有全局依赖性和局部依赖性的空间特征以及长期时间特征,研究结合LSTM网络与数据的空间特性构建了基于自注意力机制的双向LSTM插值模型SL-BiLSTM-SA。
技术路线
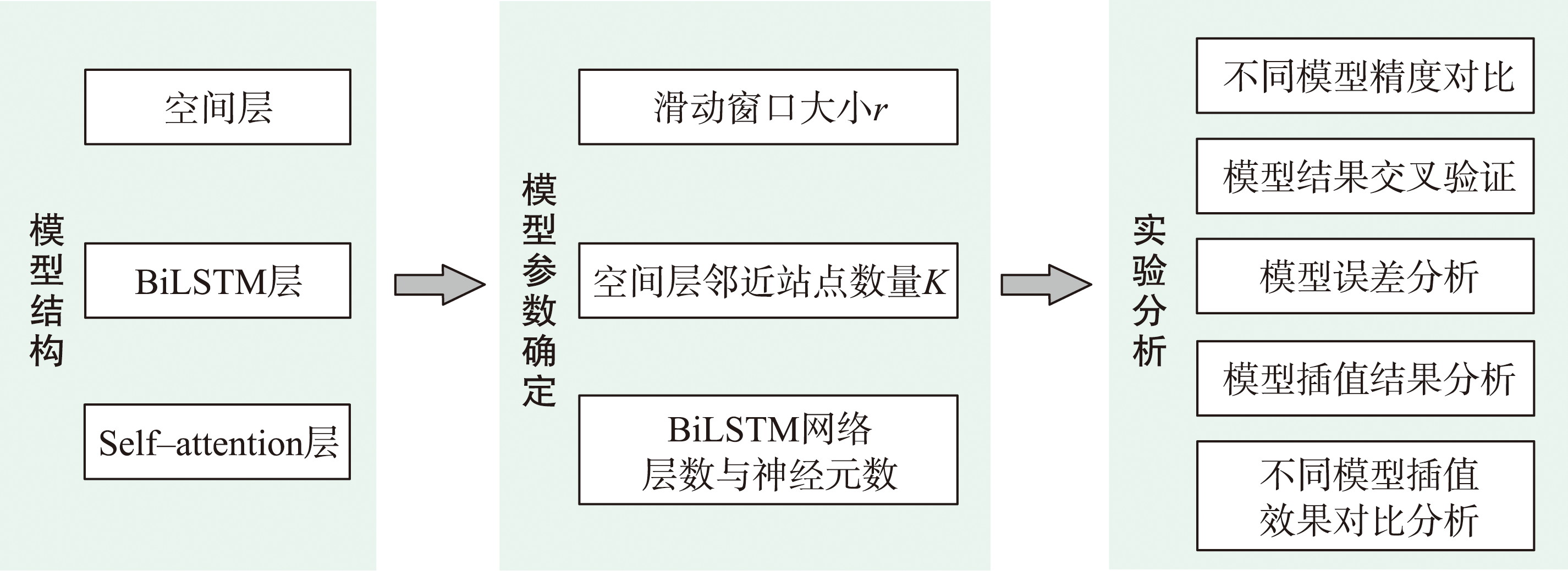
图1 SL-BiLSTM-SA插值方法的技术路线
2.1 空间层设计
在输入层后加入空间层以充分考虑数据的空间相关性,由地理学第一定律可知,已知点和未知点之间的相对位置将影响空间上的联系强度。
空间层旨在选择与未知点相关性强的观测点,并剔除相关性较弱的观测点,其结构如图3所示,Calc_d表示时空点数据之间的空间距离计算;Rank表示对计算出的空间距离进行排序。
计算过程可由式(1)表示:
soutt = MA × sint
式中:sint是空间层的输入;MA是空间层的激活矩阵;soutt为空间层的输出。

图2 筛选强空间相关信息的空间层结构
2.2 BiLSTM层设计
时空数据当前值可能对未来时刻产生影响,因此在时空插值过程中,考虑时间维度的影响是必要的。传统ANN模型无法联系前一时刻与下一时刻的信息。
与ANN模型相比,RNN将前一时刻的输出作为下一时刻的输入,实现了时序信息的传递,但RNN不能捕获时序数据中的长期相关性,甚至会导致梯度消失和梯度爆炸问题。
针对RNN局限性,LSTM引入了自连接单元,允许保留流入单元的值或梯度,并在需要的时间步长进行检索,从而保留长时间记忆信息。
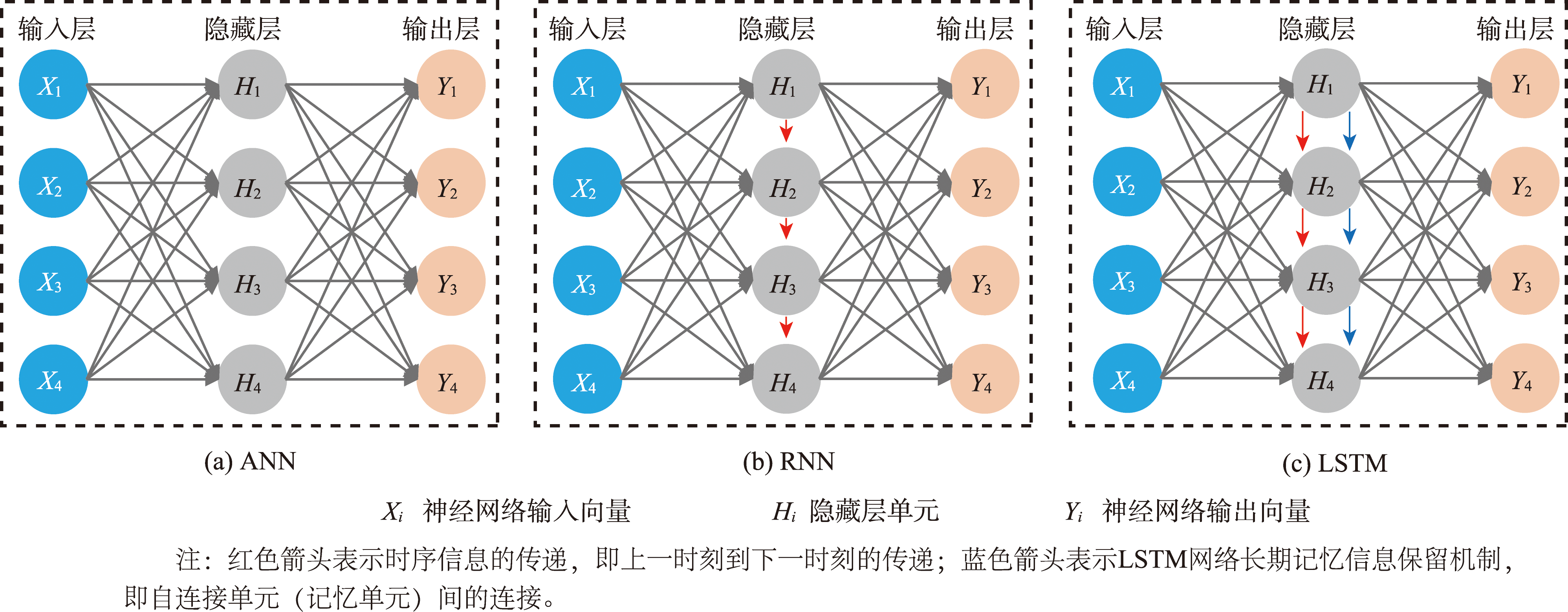
图3 ANN、RNN和LSTM结构对比
2.3 Self-attention层设计
在每个时间步,自注意力模块可以对所有位置的特征进行加权求和,以选择性地聚集每个位置的输入特征,使模型可在垂直交叉堆叠的多层LSTM中,以及在LSTM单元状态的横向传递过程中捕获全局空间依赖性。
Self-attention层的计算如式(3)、式(4)所示:
H = tanh(SA(h))
y = Σ tanh(H)
式中:h代表BiLSTM层的输出向量;SA表示自注意力机制模块;tanh为激活函数;H是通过自注意力模块聚合的特征向量,预测值y即SL-BiLSTM-SA模型的输出。
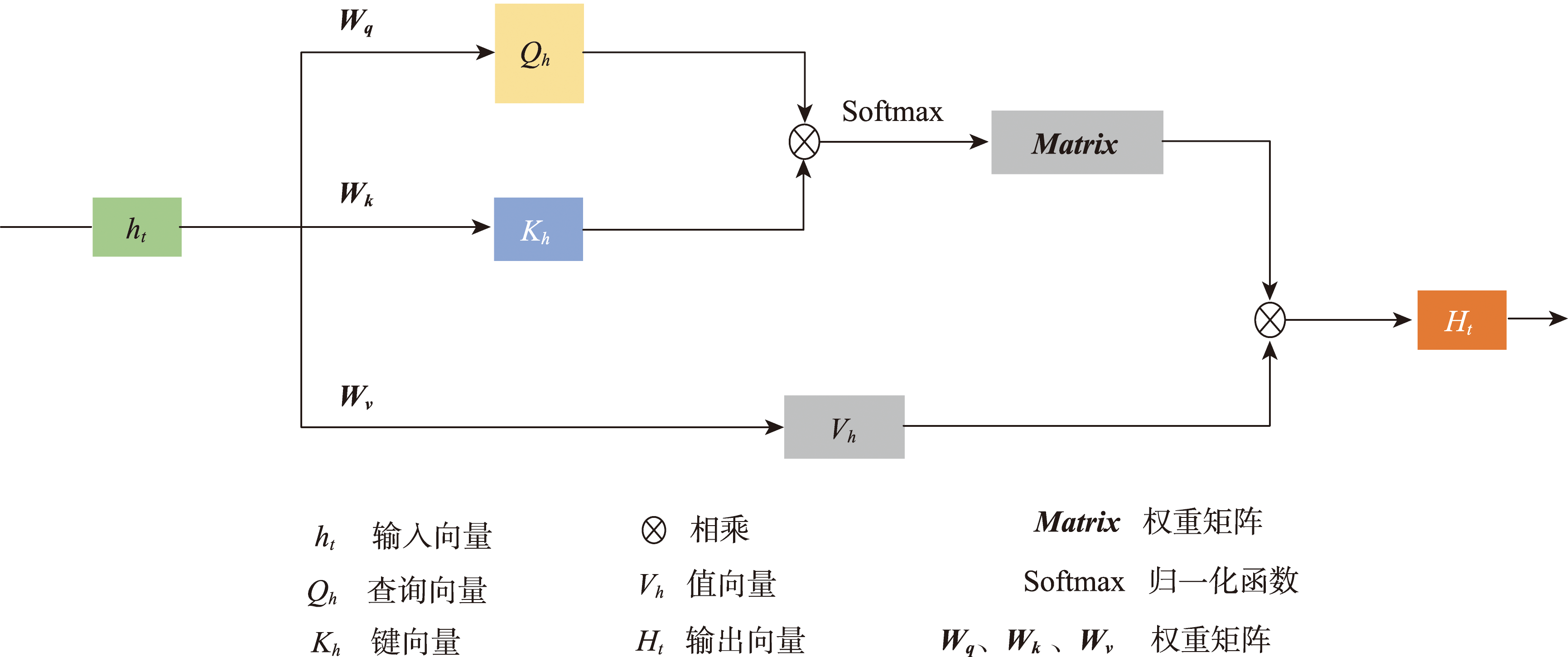
图4 自注意力机制结构
3 实验与分析
3.1 研究区域及数据来源
本文使用PM2.5浓度数据集作为时空插值方法的应用数据集。PM2.5的研究对监控和治理环境问题、探索空气污染来源和评估居民健康风险均有重要意义。
选择山东省作为研究区域,山东省属于暖温带季风气候,降水相对集中,在环境问题中雾霾造成的危害最为严重。研究使用山东省国控空气质量监测站点2020年11月1日—2021年1月31日的空气质量监测数据,共92天,剔除缺失数据较多的监测站点后共使用91个站点。
这些站点遍布在山东省16个地级市内(图8),其覆盖范围基本可以反映山东省的空气质量状况。山东省矢量化地图来源于国家基础地理信息系统数据库,原始监测数据采用CGCS_2000地理坐标系,为便于插值计算,采用高斯-克吕格投影统一将地理坐标转换为平面坐标。
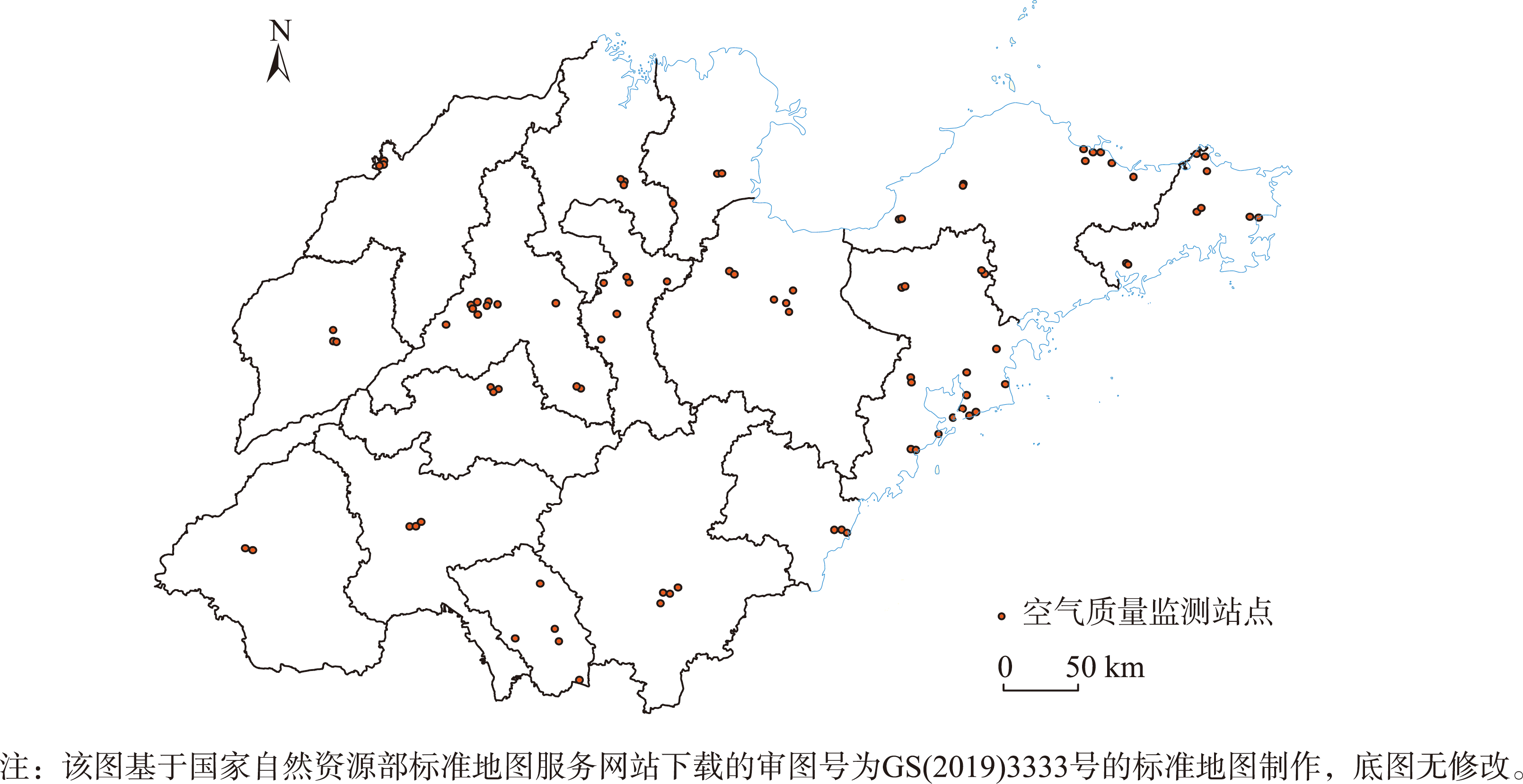
图5 山东省国控空气质量监测站点分布
3.2 数据预处理
在对山东省PM2.5浓度数据收集和清理后,采用滑动窗口法对各监测站点数据进行时间序列建模,滑动窗口由窗口长度和滑动步长组成。
图10示例了窗口长度为3、滑动步长为1构建的时间序列样本,其中窗口长度、滑动步长单位均为"一天"。
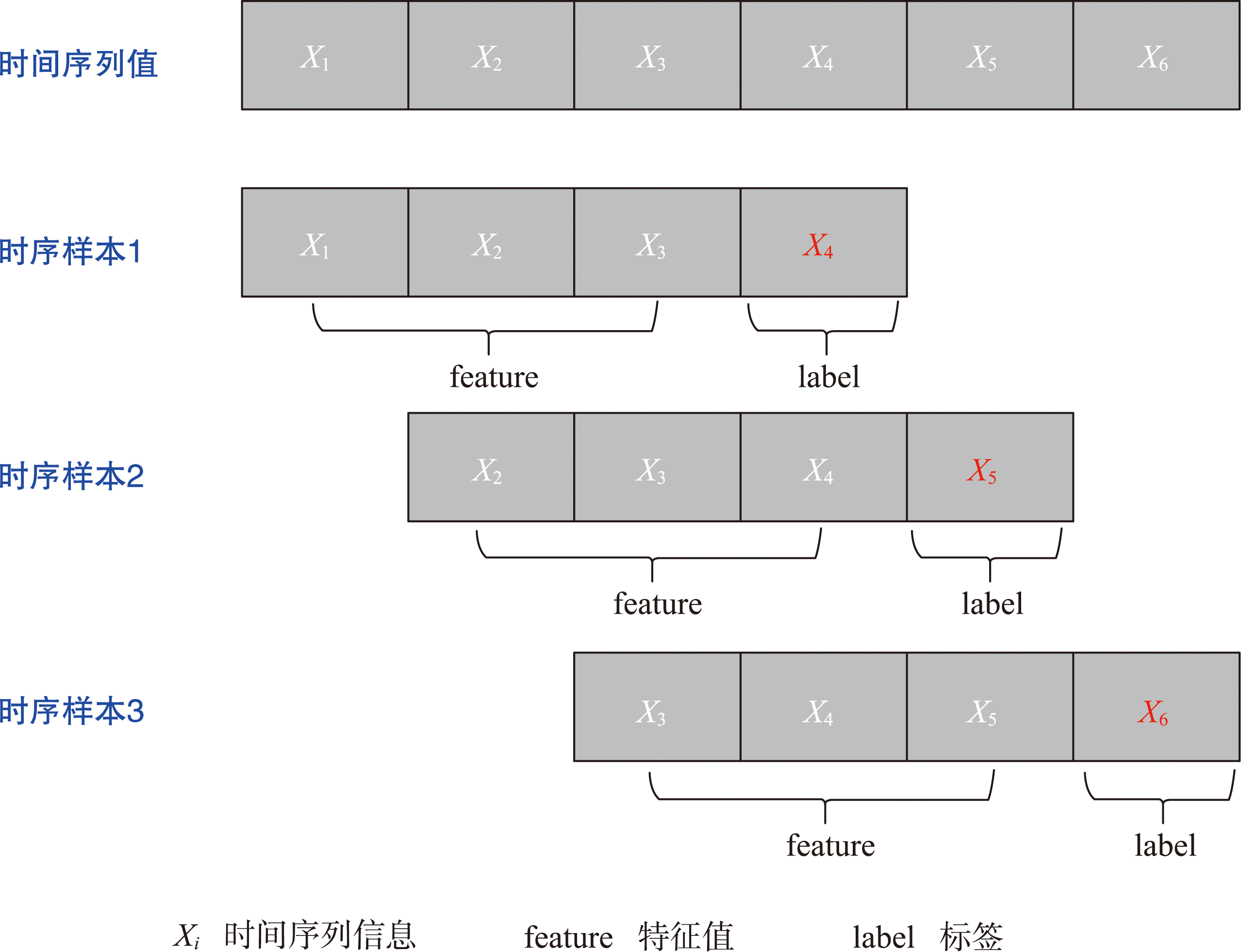
图6 窗口长度为3且滑动步长为1的时间序列样本示例
3.3 实验设计与实现
将构建的时间序列样本输入到SL-BiLSTM-SA模型中,通过训练与测试优化模型结构和参数,最终应用于山东省PM2.5浓度插值,对模型时空插值性能进行分析,并与其他插值模型进行对比。
参数优化
假设滑动窗口长度r=3,每个站点将有90个时间序列样本,91个站点则对应91×90个样本总量。为实现模型的最佳插值性能,首先需确定滑动窗口长度r、空间层邻近站点数量K等参数。
考虑到山东省内PM2.5监测站点分布不均匀,以等间隔策略设置4个K候选值{2,6,10,14}和4个窗口长度r候选值{3,5,7,9},使用网格搜索法对r和K的不同组合进行测试。
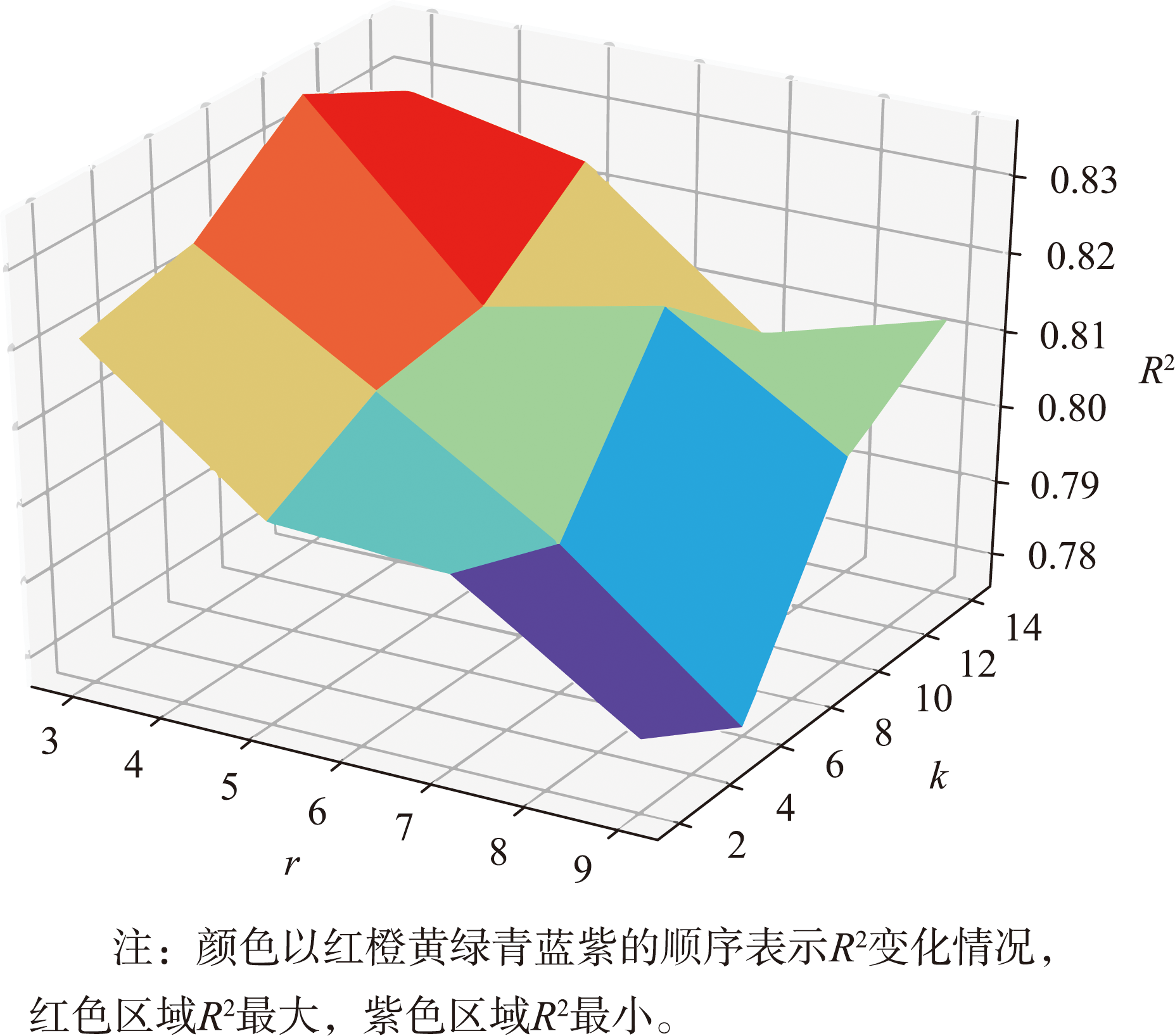
图7 在邻近站点数K和滑动窗口长度r不同组合下R2变化情况
BiLSTM结构优化
除站点数量K和滑动窗口长度r外,BiLSTM模型的层数和每个BiLSTM层神经元的数量也会对模型的插值性能产生较大影响。同样采取不同预选值组合的方式进行筛选,BiLSTM层数的预选值为{1,2,3,4,5},BiLSTM每层的神经元数量应设置为相同,预选值为{16,32,64,128,256}。
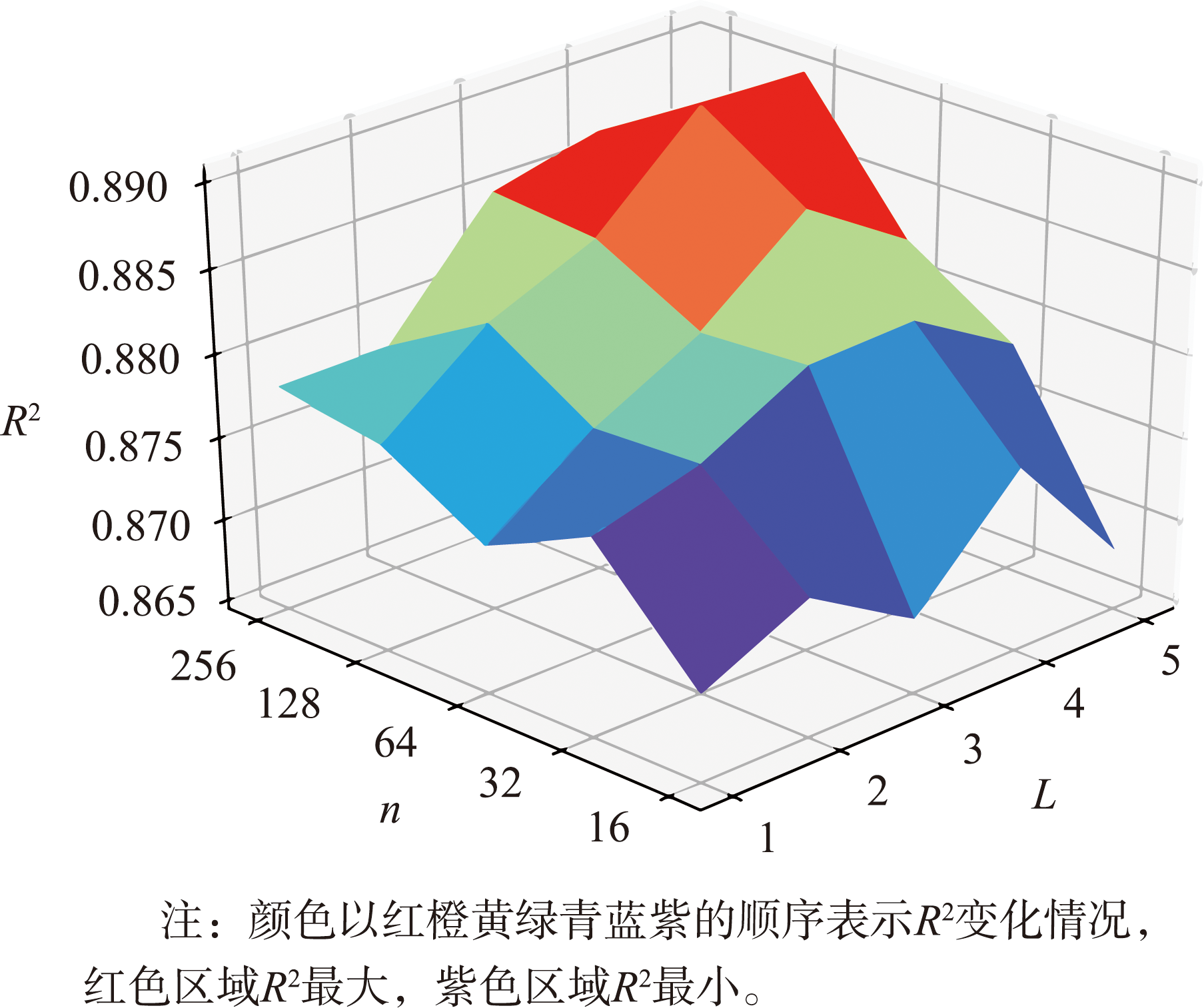
图8 在BiLSTM层数和每层神经元数量不同组合下R2变化情况
模型训练
SL-BiLSTM-SA模型通过随机均匀初始化每层参数,并使用激活函数Sigmoid模拟每个神经元的非线性输出,样本数据集按照75%、25%比例划分训练集和测试集,损失函数采用均方误差MSE,优化方法选用Adam优化器,学习率预设为0.001,训练批次大小设置为32,测试批次大小设置为16,训练轮次epoch设置为1000。
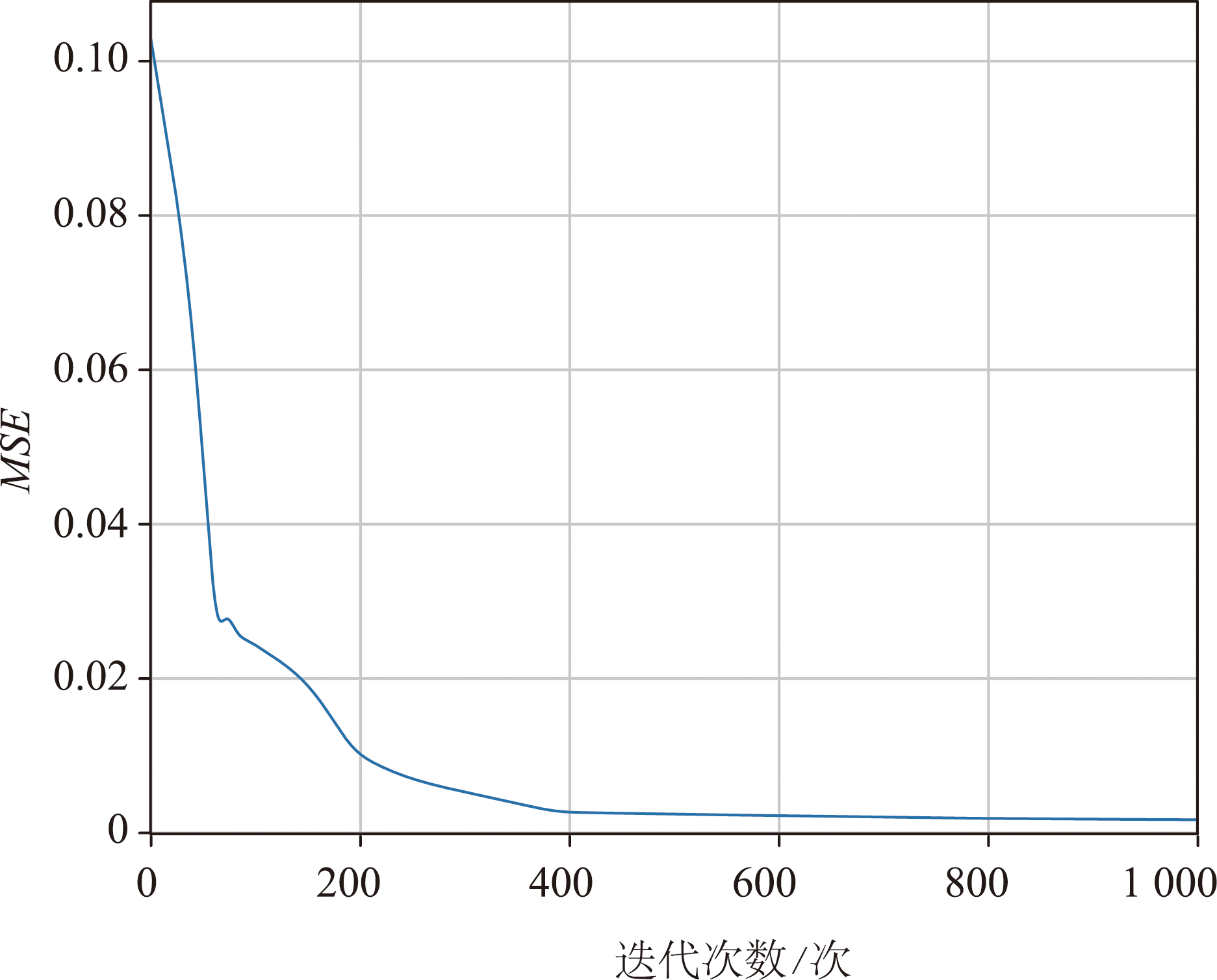
图9 模型损失函数值随迭代次数的变化
3.4 实验结果与分析
将测试集输入经过训练的模型中,通过R2、均方根误差RMSE、平均绝对误差MAE和平均绝对百分比误差MAPE衡量其插值性能,并与STOK、GA-STK和融合空间信息的LSTM模型SL-LSTM进行插值性能比较。
SL-LSTM模型和SL-BiLSTM-SA模型均对PM2.5浓度数据有较高的拟合精度。相较STOK模型,SL-LSTM模型和SL-BiLSTM-SA模型的RMSE分别降低了37.87%、39.83%,MAE和MAPE也均有不同程度的降低,总体精度有所提升。
比较结果中SL-BiLSTM-SA模型表现最好,因为其不仅考虑了站点前后时刻的时间相关性,还考虑了全局的空间相关性。
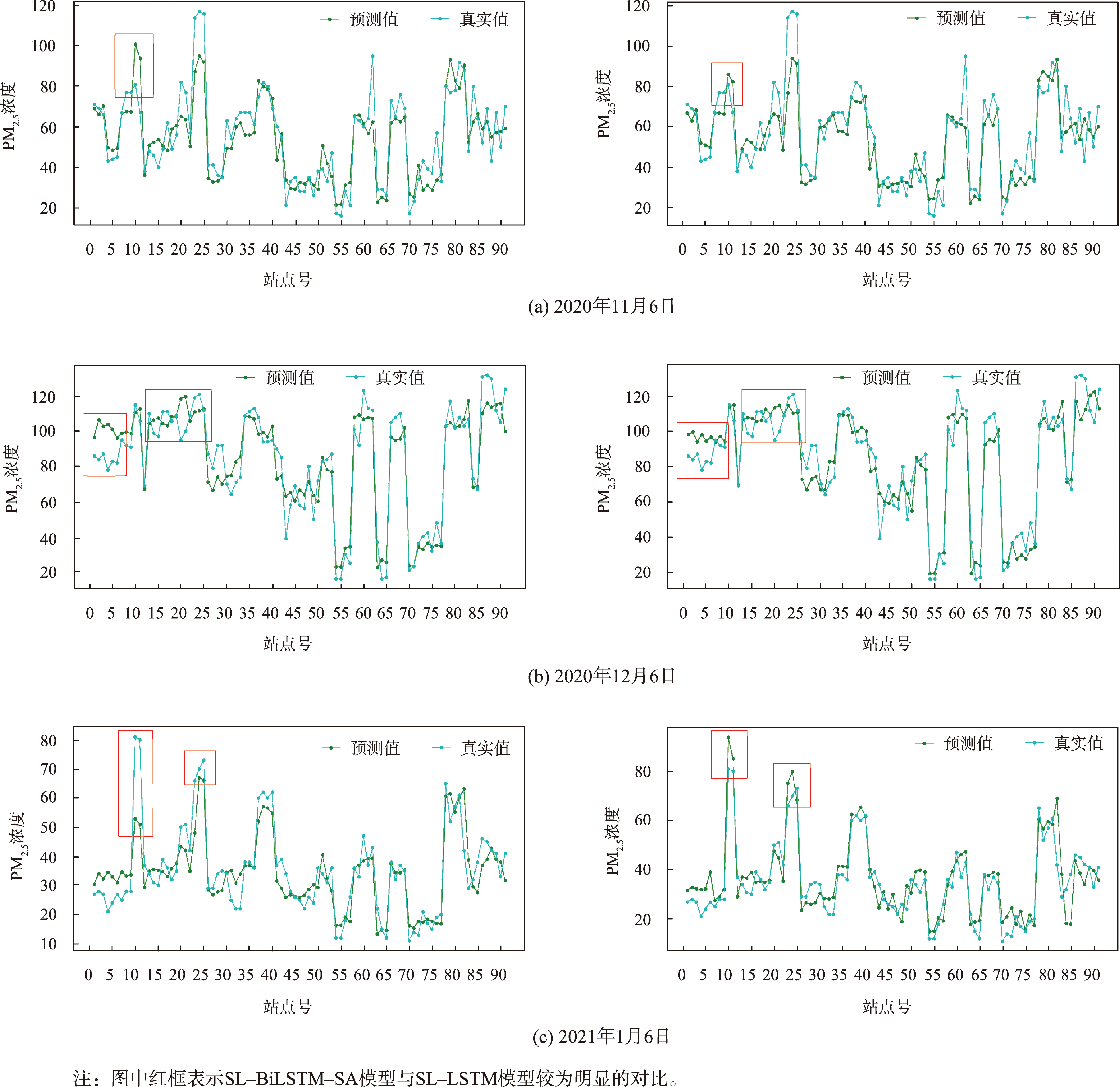
图10 SL-LSTM(左)和SL-BiLSTM-SA(右)模型预测值与真实值对比折线图
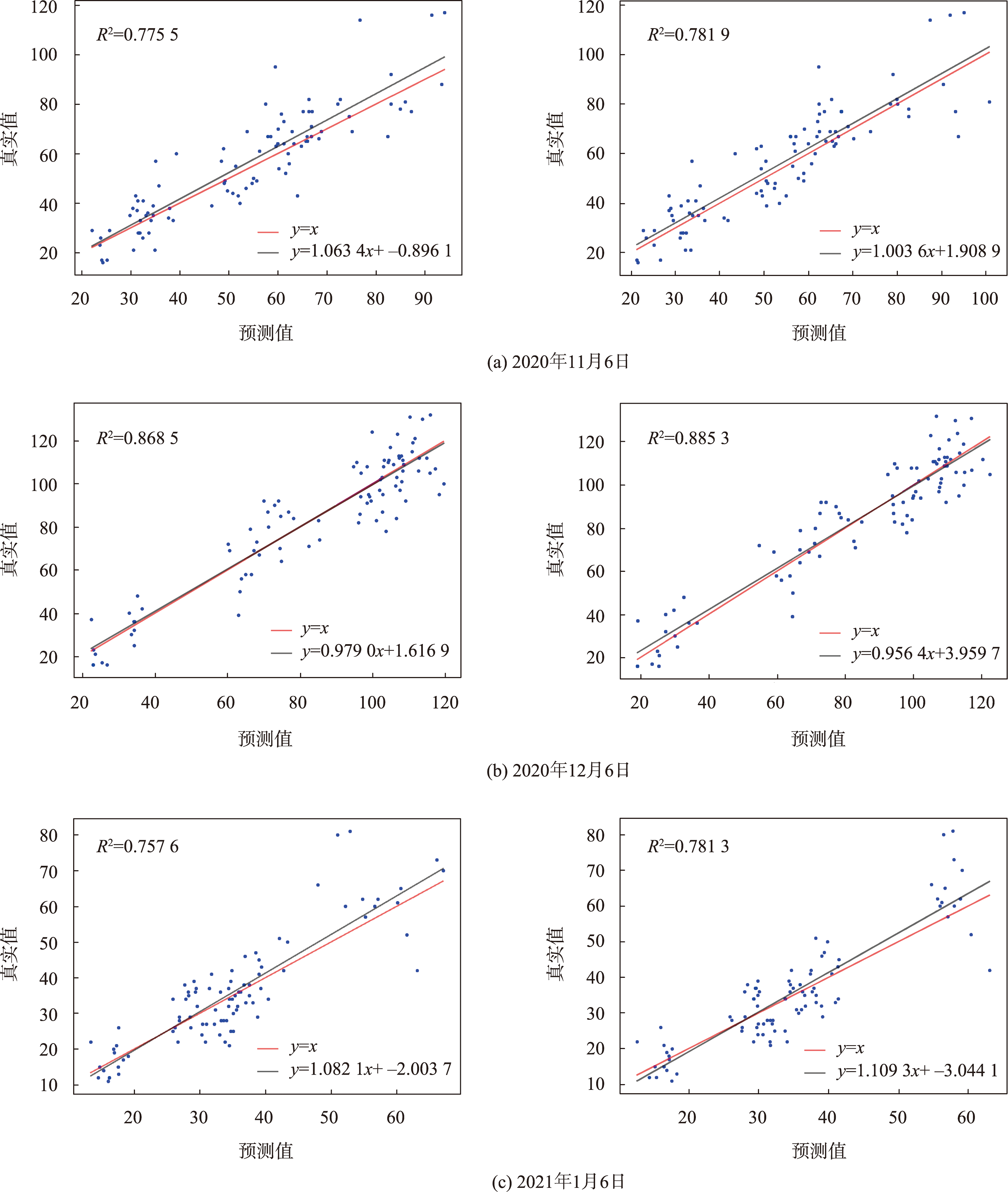
图11 SL-LSTM(左)和SL-BiLSTM-SA(右)模型预测值与真实值对比散点图
为直观体现模型插值效果,使用SL-BiLSTM-SA模型对山东省PM2.5浓度数据进行插值以推断研究区域内PM2.5浓度的空间分布规律,结果见图17。
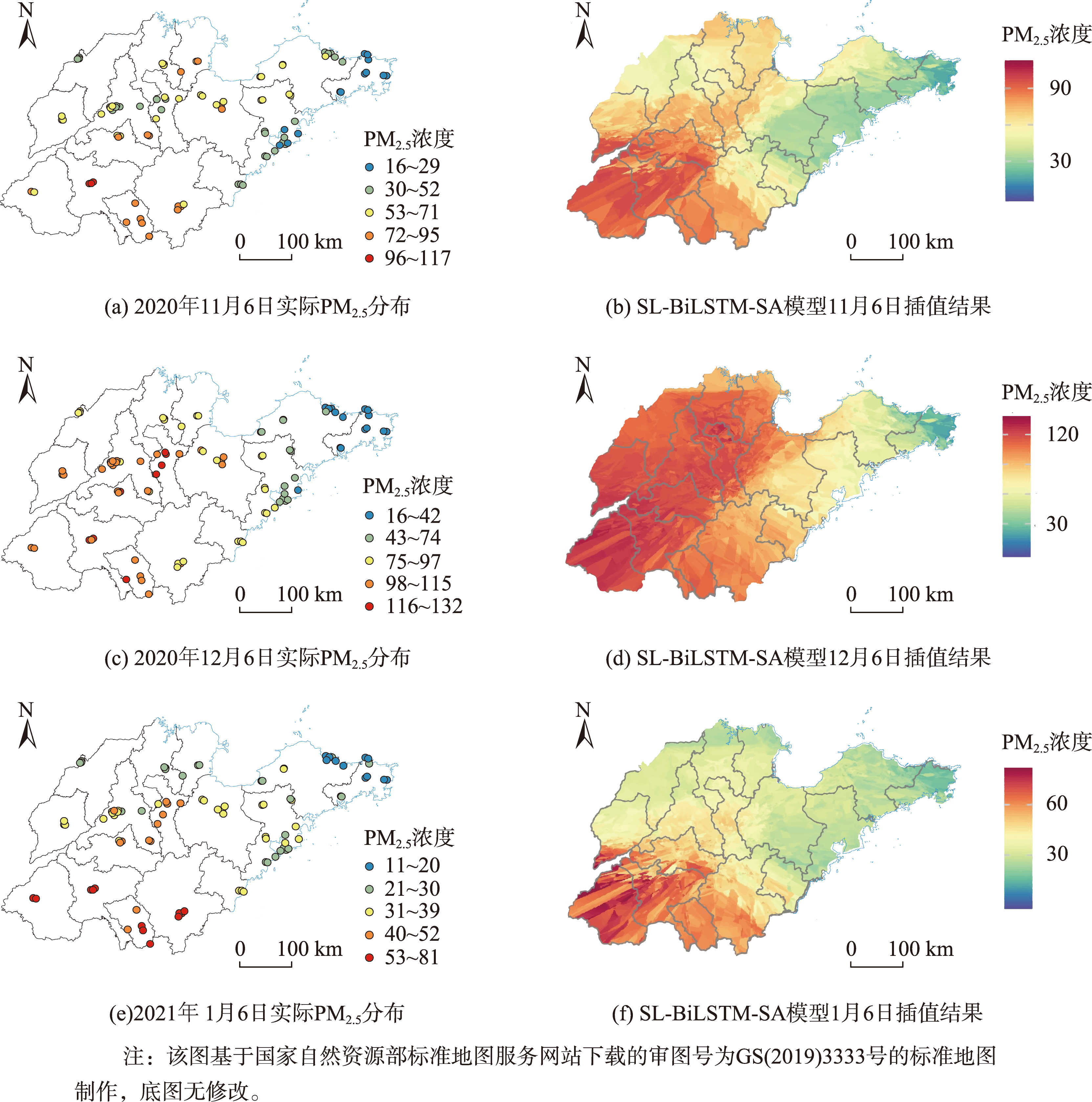
图12 SL-BiLSTM-SA模型的插值结果与实际分布比较
为比较分析不同方法的插值效果,图18展现了反距离权重IDW、STOK、GA-STK、贝叶斯最大熵BME与SL-BiLSTM-SA模型的插值效果对比。
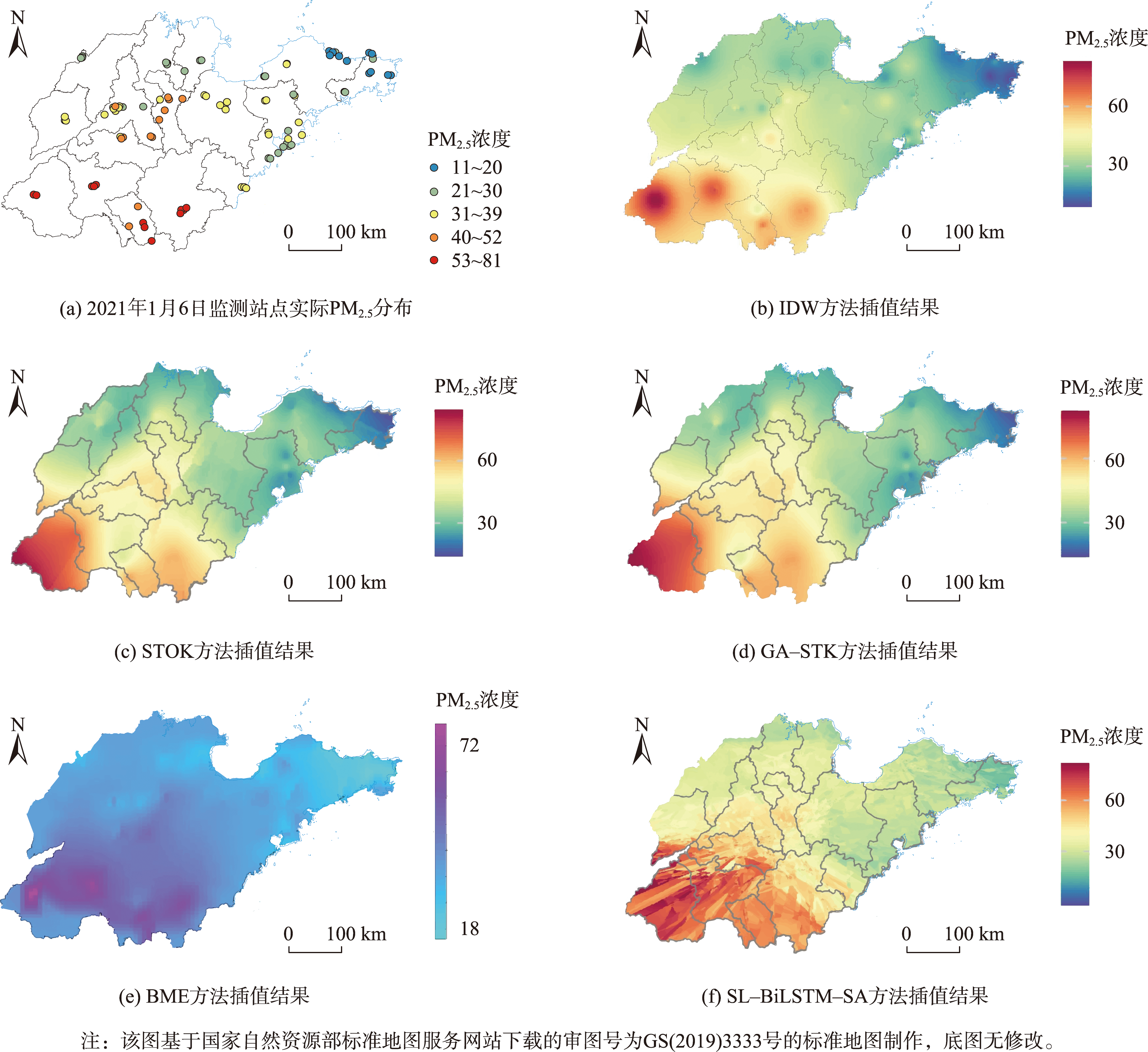
图13 SL-BiLSTM-SA模型与其他插值方法的结果对比
4 结论与讨论
传统时空插值方法存在2个方面局限:① 地统计方法,如克里金插值等,使用预先设定的线性/非线性方程定义复杂的时空关系;② 基于机器学习或深度学习的插值方法大多未同时考虑时空数据的长期时间相关性以及全局空间信息。
本文针对上述局限,设计空间层融合空间信息,引入LSTM单元以捕获长期时间依赖性并用BiLSTM网络结构替换,再添加Self-attention层捕获全局空间依赖性,构建了SL-BiLSTM-SA时空插值模型。
将模型应用于山东省PM2.5浓度数据集并与其它插值模型进行精度对比,验证了本文模型的有效性。实验表明,SL-BiLSTM-SA模型表现最好,精度与传统方法STOK、GA-STK相比分别提高了39.83%、36.63%。在分析模型插值效果时,模型能较准确地预测PM2.5浓度的高值和低值并且可以有效揭示PM2.5浓度变化的层次细节。上述实验分析说明基于BiLSTM的双向建模与Self-attention对时空数据长期时间特征和全局空间特征的捕获是有效的。
然而模型仍存在部分局限,首先,本研究通过构建时间序列样本和空间层的设计考虑了总体的时空相关性,在自注意力机制模块通过赋予不同权重考虑了时空异质性。但根据"三位一体"理论体系,当总体同时包含相关性和异质性时应优先采取分层机制去除异质性影响,论文后续将沿此方向深入研究。另外,研究因素亦受到区域中其它相关因素的影响,如模型在地势平缓地区插值时受到高程因素的影响较小,插值精度更高,因此研究后续会采用更多的相关变量辅助插值以进一步提高精度。最后,模型的滑动窗口长度、空间层邻近点数量等参数采用设定候选值与网格搜索结合的方法确定,还未实现参数的自适应调整,影响了模型的通用性,后续研究将继续改进算法,对模型进行完善与优化。