一种基于可达距离的模糊C均值聚类算法

引言

聚类算法是数据挖掘、模式识别、机器学习等领域的基础算法，是识别数据集合内部结构与数值分异的主要方法，目前已广泛应用于设施选址研究中，其主要作用是对空间数据进行地理可达性分析。地理可达性是指地理区域内不同点之间的相互关联程度，包括路网距离、交通便捷性、出行成本等属性。利用地理可达相似性聚类对空间元素进行分类是解决设施选址和服务范围覆盖等问题的重要方法。

目前已有很多研究将聚类算法应用于设施选址问题求解。聚类算法在设施选址中的主要作用是进行地理可达相似性分析，将相似性高的元素聚为一簇，簇类中心则是在地理可达维度上为该簇内所有元素提供服务的最佳位置点。

然而，这些算法大多以欧氏距离进行聚类，可达性测度准确性较低，可能导致聚类元素被划分至实际距离更远的分簇中，聚类结果误差偏大；且并没有考虑山川湖泊等地理障碍，生成的簇中心很可能位于路网之外的不可达区域，只适合在宏观角度下进行较低精准度的地理相似性分析。

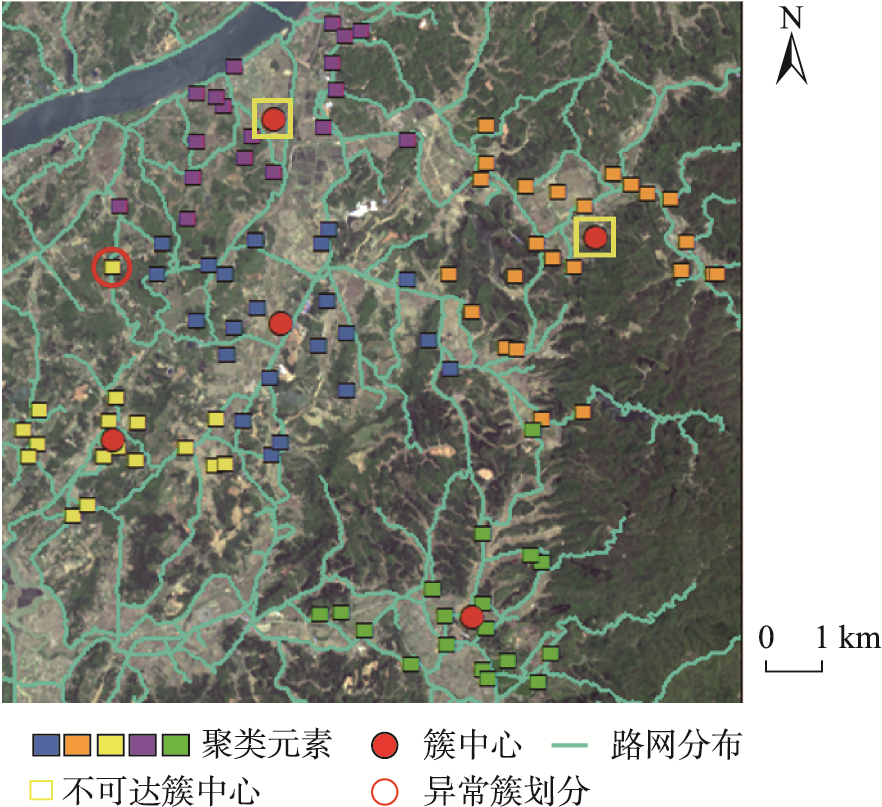
图1 标准FCM聚类算法在应用场景中的聚类结果

研究方法

2.1 问题场景与建模

面向地理可达性的聚类通常根据聚类元素间的可达距离将其划分为若干簇，使得相同簇内元素间的可达性优于非同簇元素。设施选址问题是其中的典型应用。图1展示了基于实际场景的设施选址示例，红色圆点代表设施，需对区域内所有聚类元素提供服务。目前，对空间元素进行地理相似性聚类是确定设施位置及覆盖范围的主要方法。

令C={c₁, c₂, ⋯, c_i, c_i+1, ⋯, c_d}表示簇中心(即设施位置)集合，X={x₁, x₂, ⋯, x_j, x_j+1, ⋯, x_n}表示聚类元素集合，其中c_i、x_j分别表示第i个簇中心和第j个聚类元素，n∈N*表示集合中聚类元素的个数，d∈N*且d≤n表示分簇的个数(即设施的个数)。FCM聚类算法的聚类目标函数如式(1)所示。

J = min(∑_i=1^d∑_j=1ⁿu_ij^m∥x_j-c_i∥²), s.t. ∑_i=1^du_ij=1, j=1,2,⋯,n

2.2 基于可达距离的模糊C均值聚类算法

FCM-RD算法将基于路网的可达距离作为地理相似性度量指标，改造了经典FCM算法的目标函数、隶属度函数和簇中心计算函数；并根据预先指定的簇划分数初始化可达簇中心集合，将聚类元素投影到路网上，设计了满足地理可达性的簇中心迭代机制，实现了基于可达距离的聚类，并在迭代过程中生成可达簇中心。

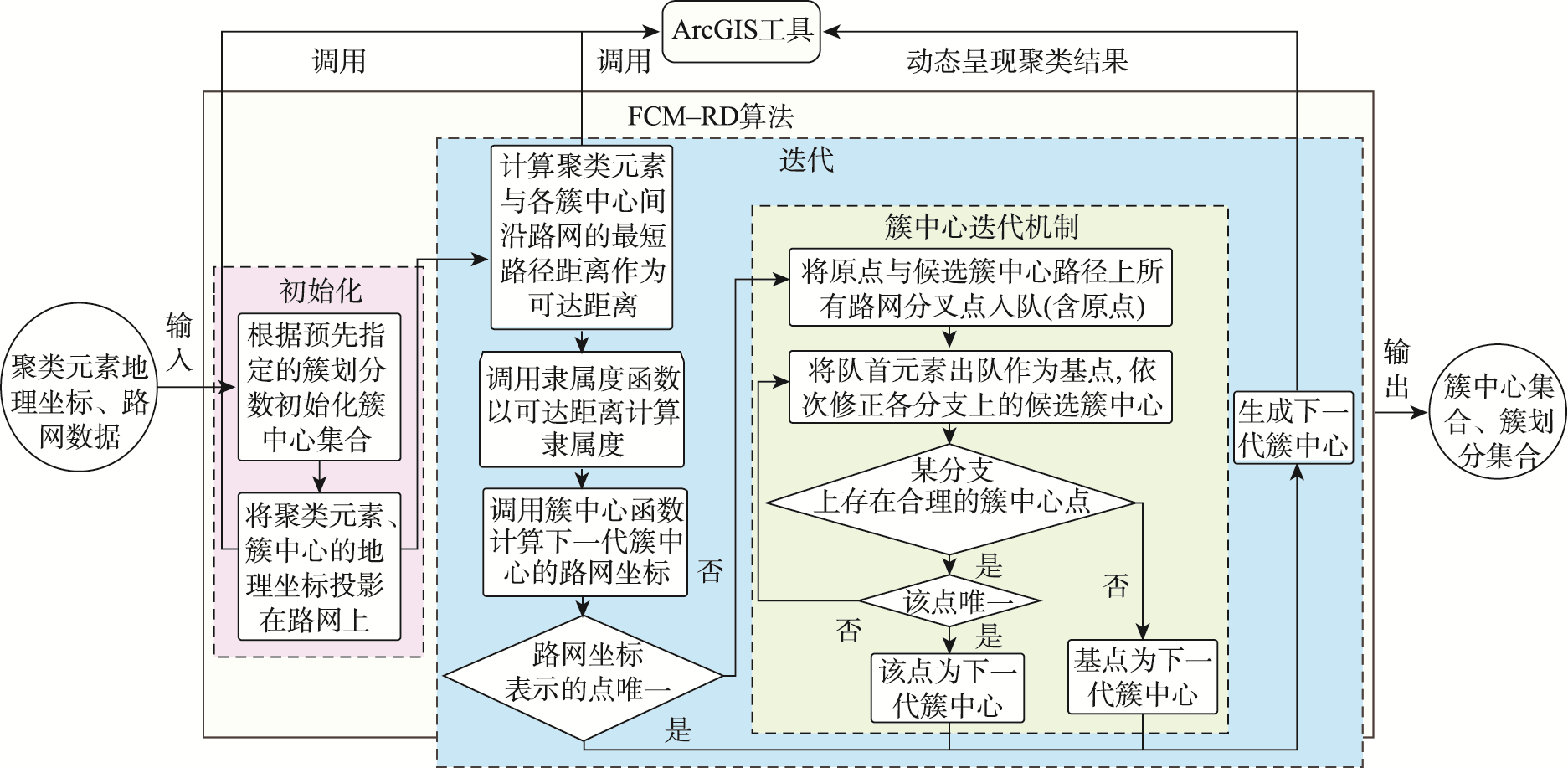
图2 FCM-RD算法整体框架

场景实验

3.1 实验设计

实验场景为湖南省某县一实际业务场景，其中遥感影像来源于开源下载；路网数据来源于商业购买，包括农村公路及普通国、省道数据；预处理阶段已删除重复以及无意义的线段，补齐缺失不连通的线段；聚类元素原始数据为文本地址信息，预处理过程中通过地址匹配加地理编码技术转换为空间坐标。

实验选用5种度量指标来评估聚类性能：所有聚类元素距其所属簇中心最短可达距离的均值、最大值、最小值、Davies-Bouldin Index(DB指数)、Silhouette Coefficient(轮廓系数)。

3.2 实验结果分析

为验证FCM-RD算法在每次迭代中所选簇中心为当前簇类目标函数最小值点，随机在某轮迭代后簇中心左右两边均匀采点并计算采样点的簇类目标值。图5展示了本文八组聚类场景中随机选取的某一轮迭代过程的采点取值结果。

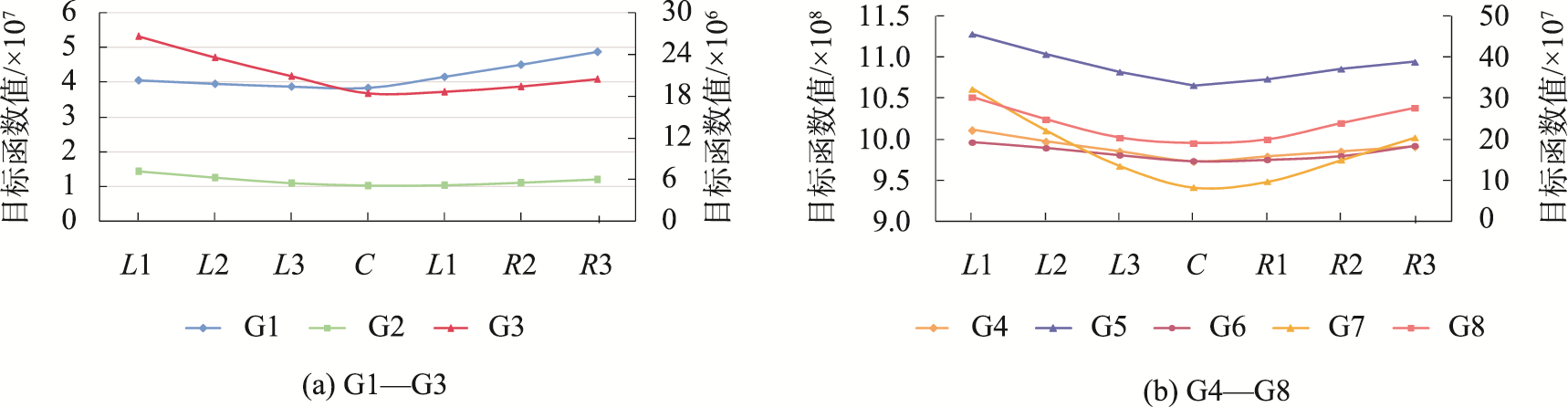
图3 FCM-RD簇中心有效性验证结果

图6给出了FCM-RD算法在各组实验中的可视化聚类结果。其中，红色圆点表示簇中心，相同颜色的正方形点表示同一簇中的样本点。由图可知，FCM-RD算法将聚类元素按照路网距离将其划分到最近簇中心，且算法所选到的簇中心始终位于路网上。

图4 FCM-RD部分聚类结果

本文还分别对八组实验中的簇中心位置进行了统计，如表2所示，FCM-RD所选到的簇中心100%位于路网上，而欧氏FCM、均值漂移算法所选到的簇中心均位于路网之外的空地上或不可达区域。

图7展示了两种算法在实验中的平均每代目标函数值，横轴表示迭代次数，纵轴表示目标函数值。由图可见，FCM-RD聚类算法的收敛速度与欧氏FCM聚类算法相当。

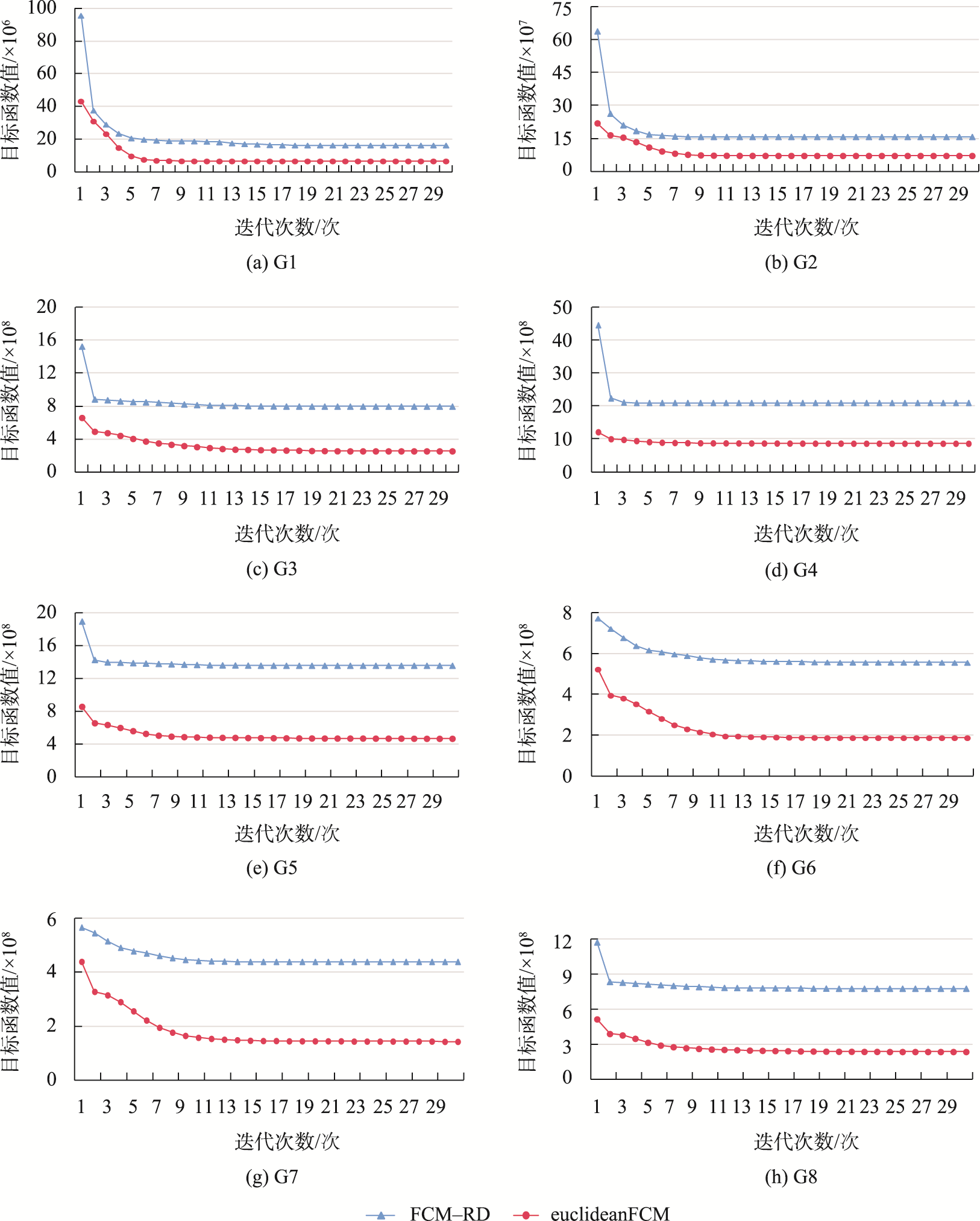
图5 算法收敛速度对比

结论与讨论

4.1 结论

鉴于现有的面向地理可达性的聚类算法存在忽略地理障碍、簇中心受限等缺陷，本文提出了一种基于可达距离的模糊C均值聚类算法(Fuzzy C-Means based on Reachable Distance, FCM-RD)。算法的创新包括：

改造基于欧氏距离的FCM算法的目标函数、隶属度函数和簇中心函数，将聚类元素间沿路网的最短路径距离作为可达距离，以可达距离衡量数据元素间的地理可达相似性，克服传统聚类算法在处理地理空间数据时的局限性，提升聚类结果精度；
将聚类元素的二维地理坐标映射为平面路网坐标，以实际可达距离衡量元素地理相似性，以路网坐标计算簇中心位置，便利簇中心计算且确保簇中心可达；
设计基于可达距离的簇中心迭代机制，确保簇中心唯一且为簇类目标函数最小值点，并对所选取的簇中心的有效性进行了数学分析和实验验证。

与基准算法的对比实验也表明，FCM-RD算法在可达距离均值、最大值指标上均有性能提升，部分性能提升甚至达到38.9%；少部分实验在DB指数和轮廓系数指标上也略有提升，且克服了现有聚类算法在真实场景中地理可达性测度不准确、聚类结果误差偏大、簇中心不可达等缺陷，为实际场景下的地理空间聚类方案提供有效且精准的解决方案。

4.2 讨论

据作者所知，FCM-RD算法是首个以可达距离聚类并在聚类过程实现不受约束的可达簇中心的聚类算法，为设施选址、服务范围划分等问题提供了有效求解工具。相比于现有的应用"二步法"求解考虑多业务因素的设施选址问题的相关研究，FCM-RD算法可以确保初始设施位置可达且为真实地理可达性下的最优选择。

但当路网数据庞大且复杂时，FCM-RD算法的聚类精度较低，后续研究需验证FCM-RD算法在不同数据规模下的一致性和稳定性，以确保其在各种应用场景中的适用性。此外，FCM-RD算法在迭代过程中需频繁读取GIS系统中的数据，导致I/O时间过长，这类问题可从软件工程角度进行优化。