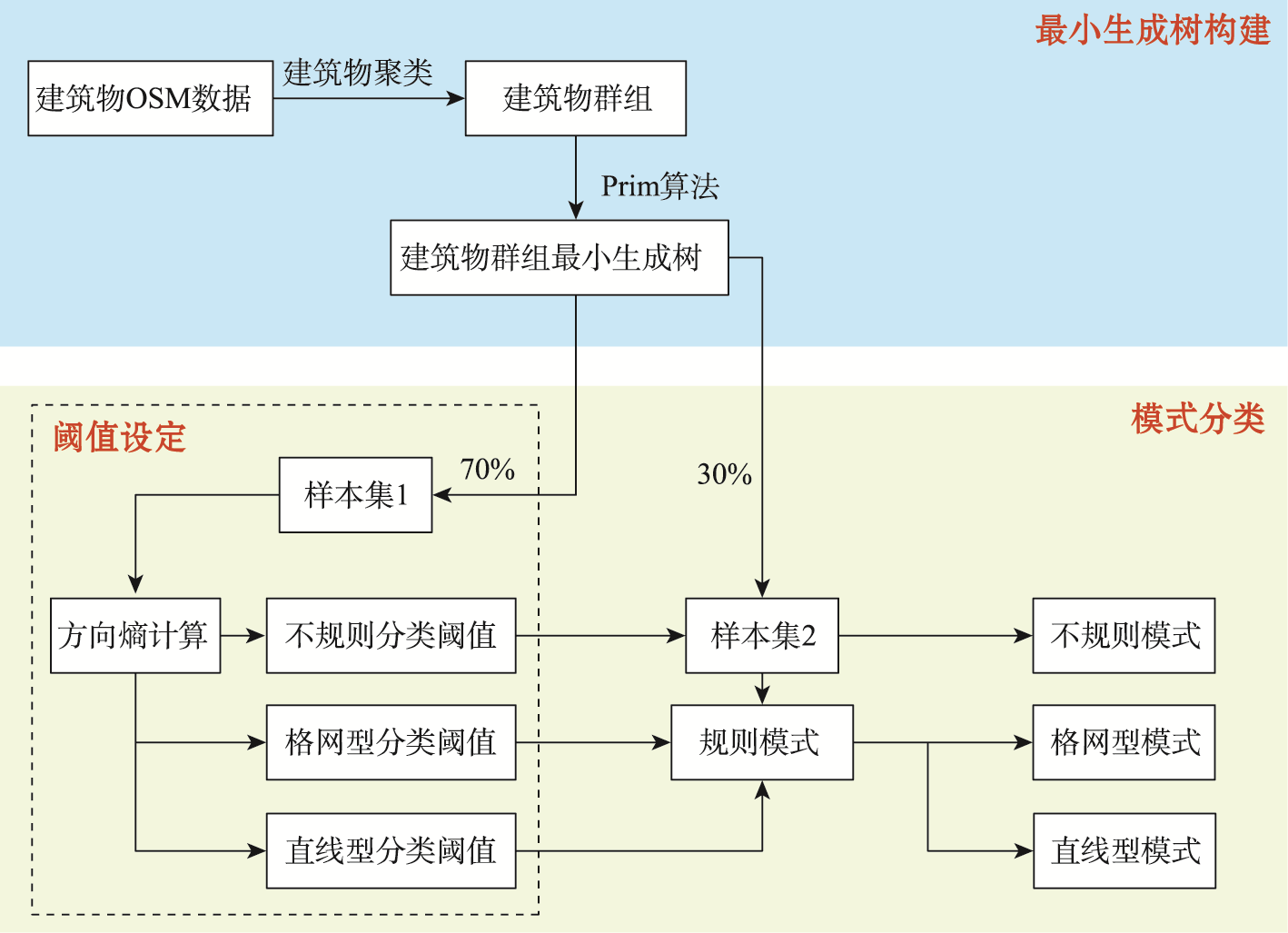
算法流程
方向熵可以很好地反映出目标空间分布的规律,对于结构化区域的识别效果较好,同时其计算不需要人为预先设定阈值。
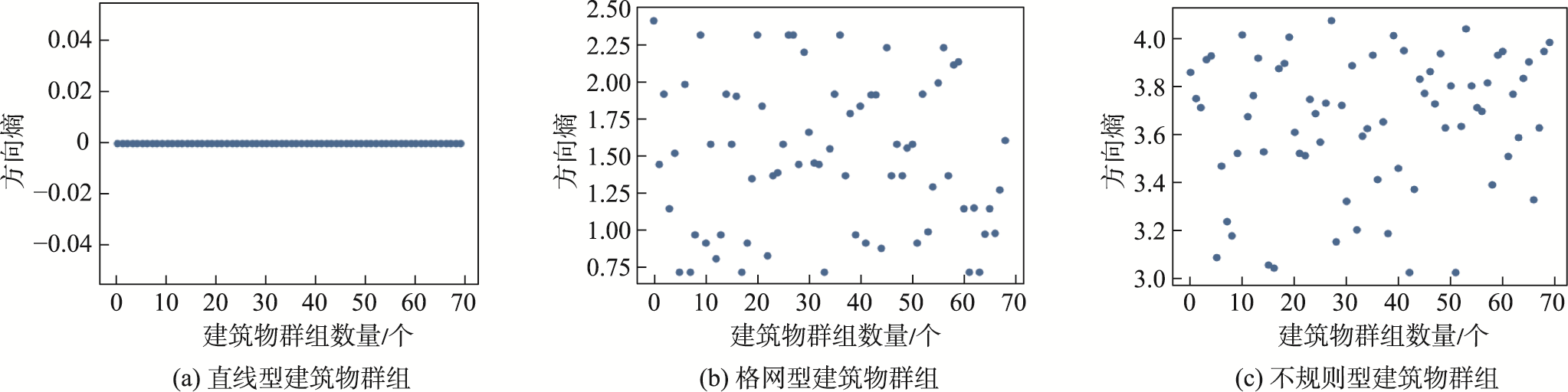
通过实验确定了3种建筑物群组模式的分类阈值:直线型方向熵值为0,格网型为0~2.5之间,不规则型为2.5以上。
实验结果显示,方向熵对于直线型、格网型和不规则型建筑物群组的分类精度均达到了97%以上,验证了方法的有效性。

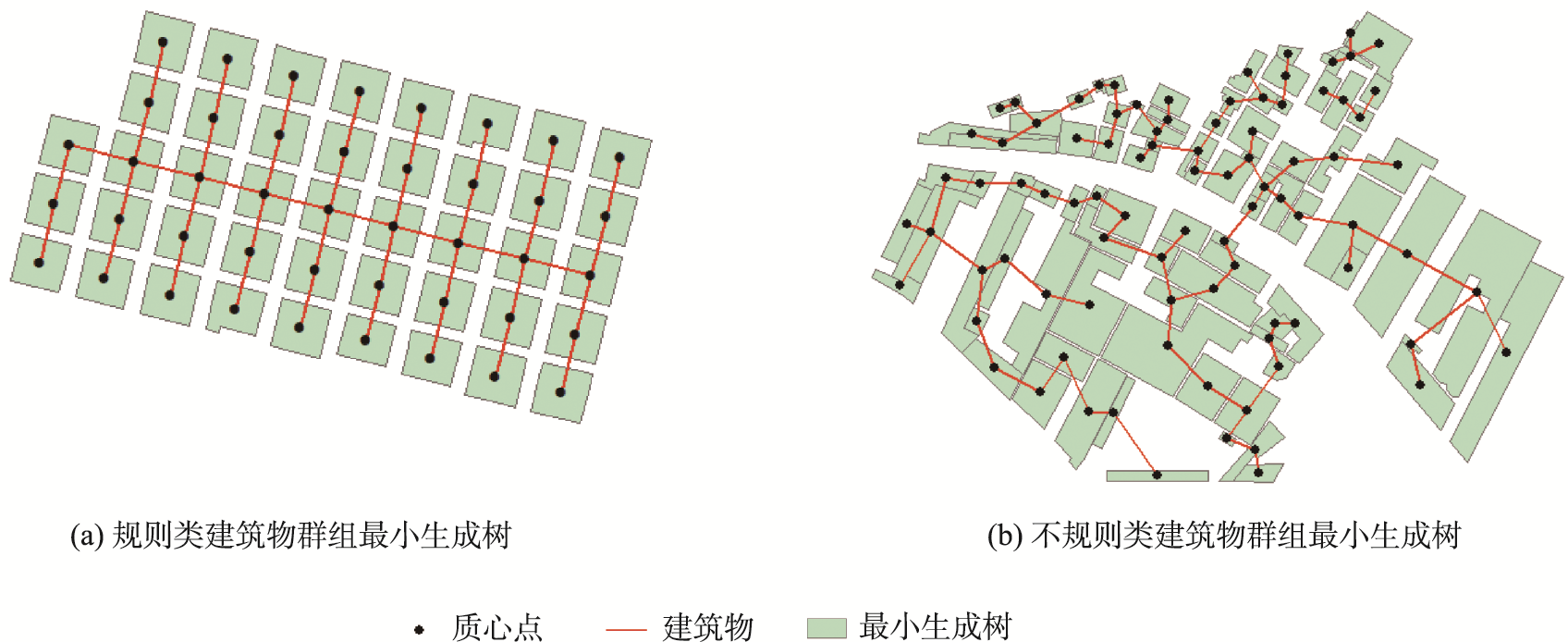
最小生成树(Minimal Spanning Tree)是将N个顶点利用N-1条边连接而成的权值最小连通子图,在本次实验中是以建筑物之间的距离作为权重。
本次实验选用Prim算法构建最小生成树,针对密集的建筑物群组时,Prim算法构建最小生成树更加高效且简单。
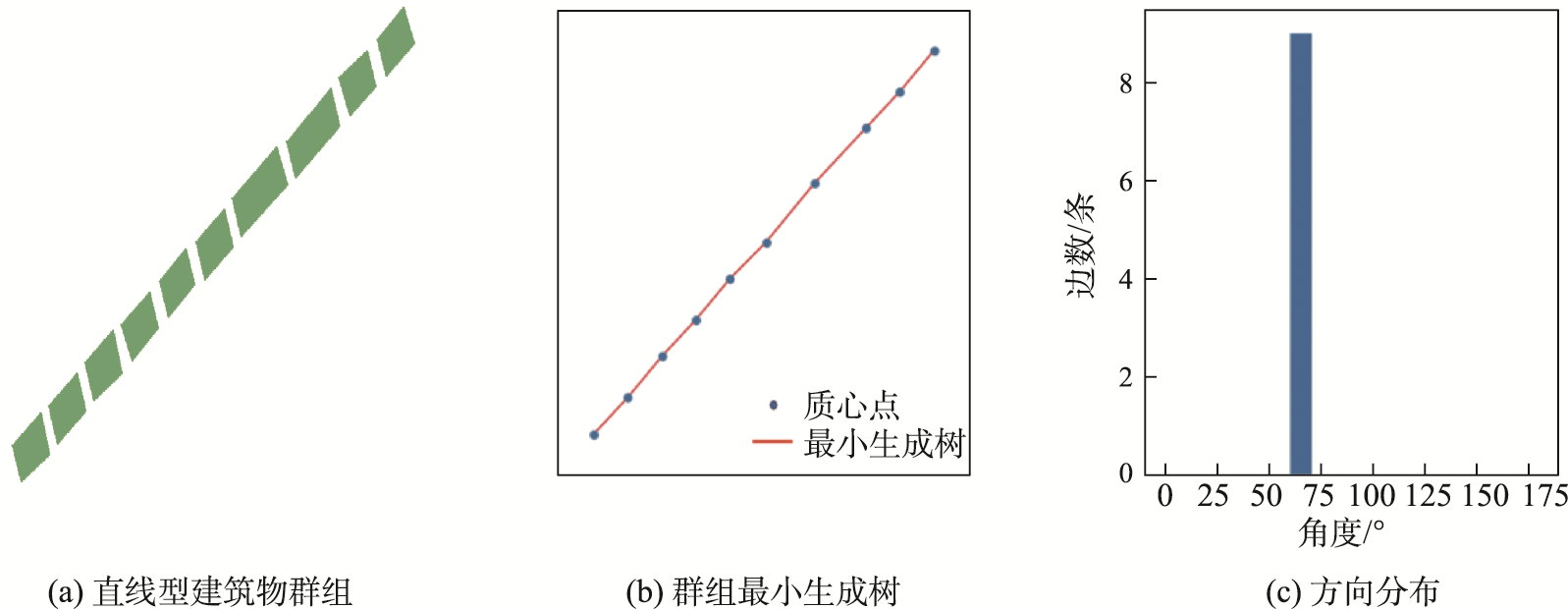
直线型建筑物群组模式是指建筑物群组在一条明显的直线上排列,其方向性分布特征主要表现为:
实验结果显示:直线型建筑物群组的方向熵熵值全部为0,因此设其判断阈值为0。
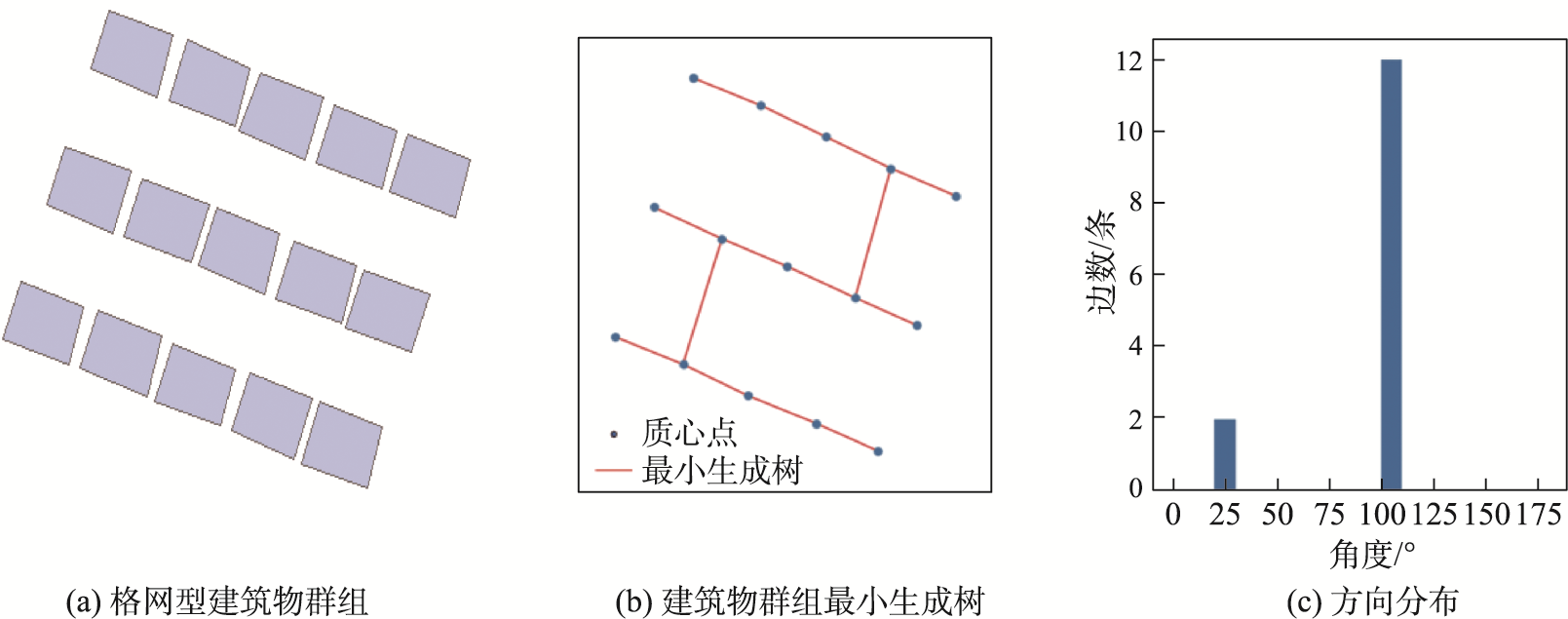
格网型建筑物群组模式主要表现为建筑物群组在二维平面上按网格形式规则排布,其方向性分布特征主要表现为:
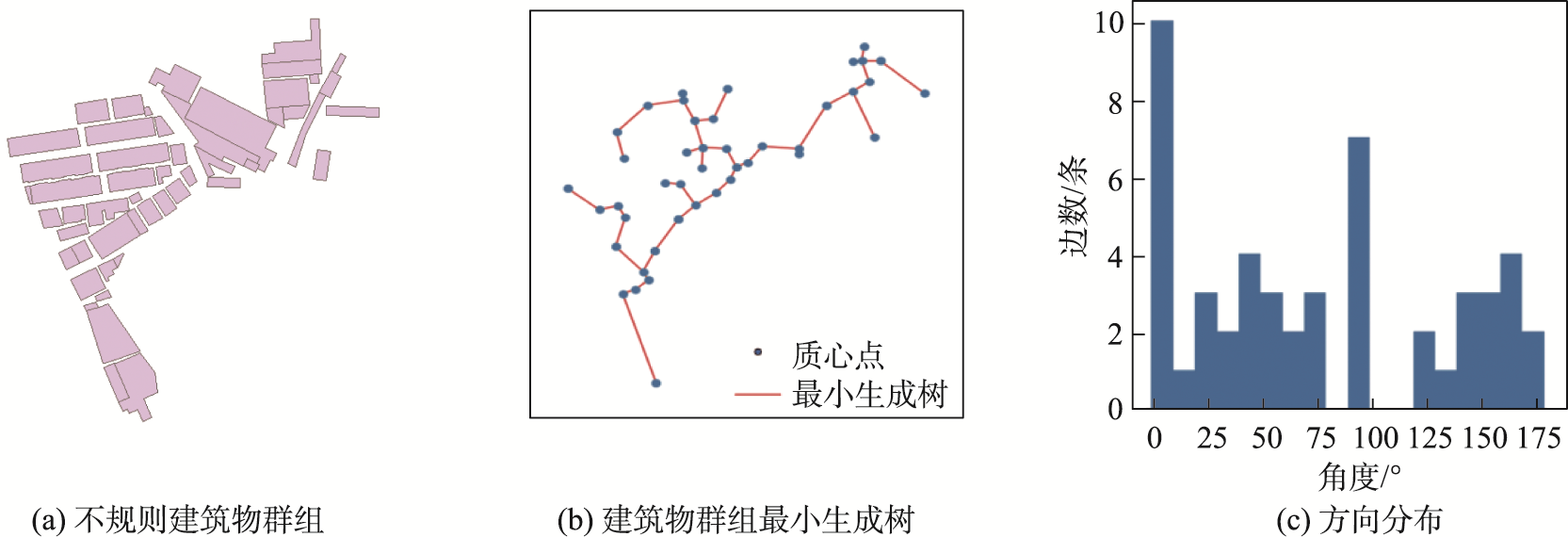
不规则类建筑物群组中建筑物的排列和空间分布较为随意,存在以下分布规律:
实验结果显示:不规则建筑物群组的方向熵熵值一般在2.5以上,因此设置阈值为2.5。
| 测试集样本 | 预测的直线型群组 | 预测的格网型群组 | 预测的不规则型群组 |
|---|---|---|---|
| 标注的直线型群组 | 27 | 3 | 0 |
| 标注的格网型群组 | 0 | 30 | 0 |
| 标注的不规则型群组 | 0 | 0 | 30 |
| 模型类别 | 识别精度 |
|---|---|
| 直线型 | 97.00% |
| 格网型 | 100.00% |
| 不规则型 | 100.00% |
将所提方法应用于上海市的建筑物数据中,获得了符合人类认知的结果,进一步验证了方向熵在群组目标分布模式识别中的有效性。
在问卷调查中发现10号直线型建筑物群组的方向熵熵值计算为0.69,导致识别出现错误。分析发现,当群组中节点之间的偏移过大时,最小生成树内部存在多个不同方向,会影响识别结果。
26号不规则型建筑物群组通过人眼识别时有点偏似格网型,但其建筑物分布离散,部分建筑物位置混乱,方向熵熵值计算为3.33,正确识别为不规则类建筑物群组。
30号建筑物群组属于辐射模式,其方向熵熵值为3.26,被识别为不规则模式。研究发现最小生成树不适用于辐射模式的识别,这将是下一步研究方向。
本研究在方向熵计算的基础上,使用较为简单的方法实现了3种典型建筑物群组的模式识别,主要创新点体现在:
将方向熵引入到建筑物模式识别研究中,克服了已有方法识别模式单一、需要人为设置阈值等不足。
通过样本集划分确定了直线型(0)、格网型(0~2.5)和不规则型(>2.5)的分类阈值。
实现了一次性识别3种建筑物群组模式,分类精度均达到97%以上。
通过换区域验证、视觉认知对比及心理问卷调查,验证了方法的有效性和可靠性。
针对辐射型等特殊建筑物模式的识别问题,下一步将探索Delaunay三角网等方法的引入,以完善建筑物群组模式识别体系。