研究背景与挑战

PM2.5数据缺失问题

我国小时尺度PM2.5约有40%的天数存在缺失，站点数据缺失率高达50%，严重影响污染现象及其演变特征解析成效。如何实现站点PM2.5数据缺失准确填补，并构建完整的PM2.5浓度数据集对提升我国环境治理能力至关重要。

现有方法局限性

  • 未能充分考虑PM2.5的昼夜周期性
  • 未顾及PM2.5自身的时空异质性
  • 采用单一机器学习模型难以有效捕捉复杂关系

研究方法

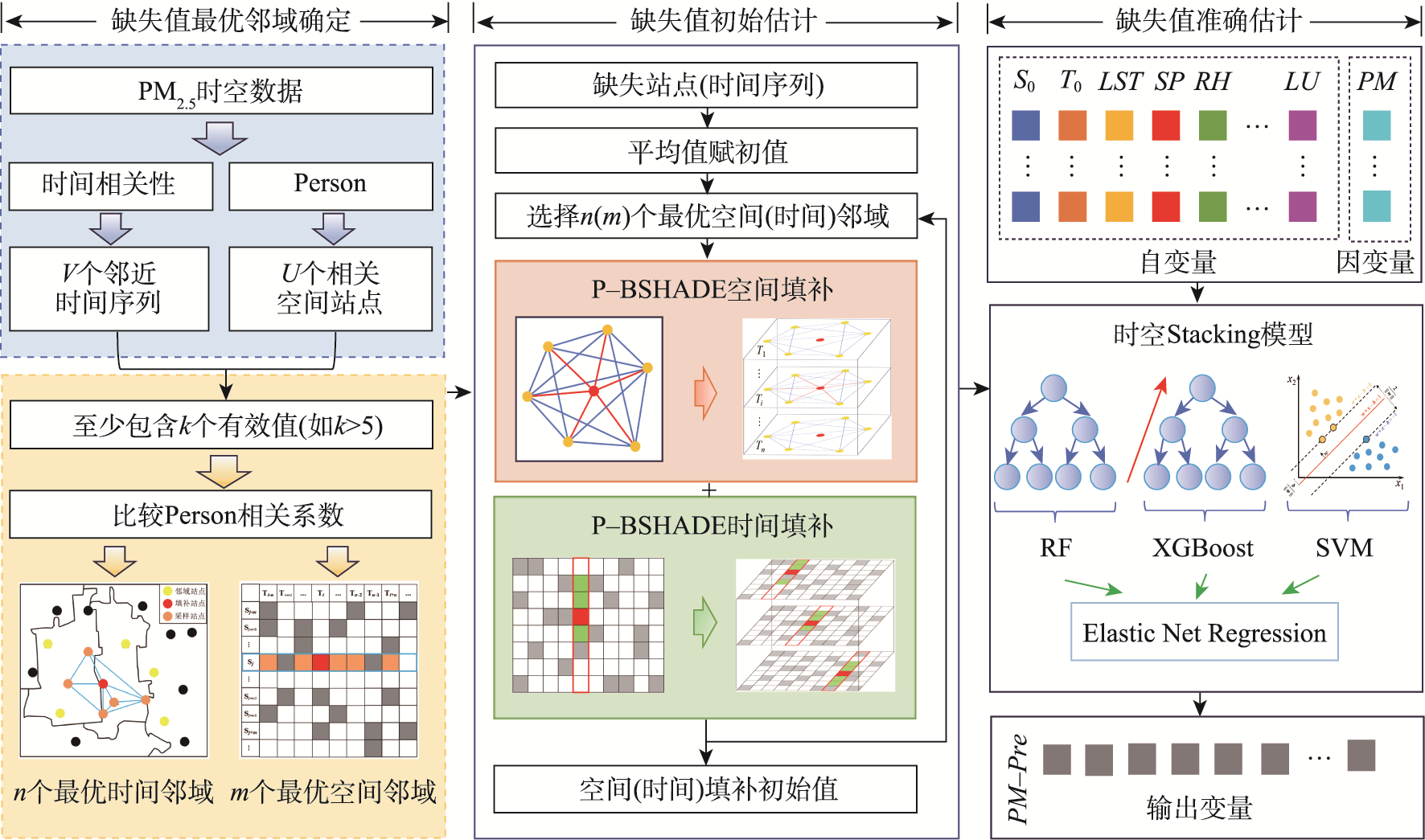
方法流程图

图1 顾及日周期性的PM2.5缺失值重构方法流程

缺失值最优邻域确定

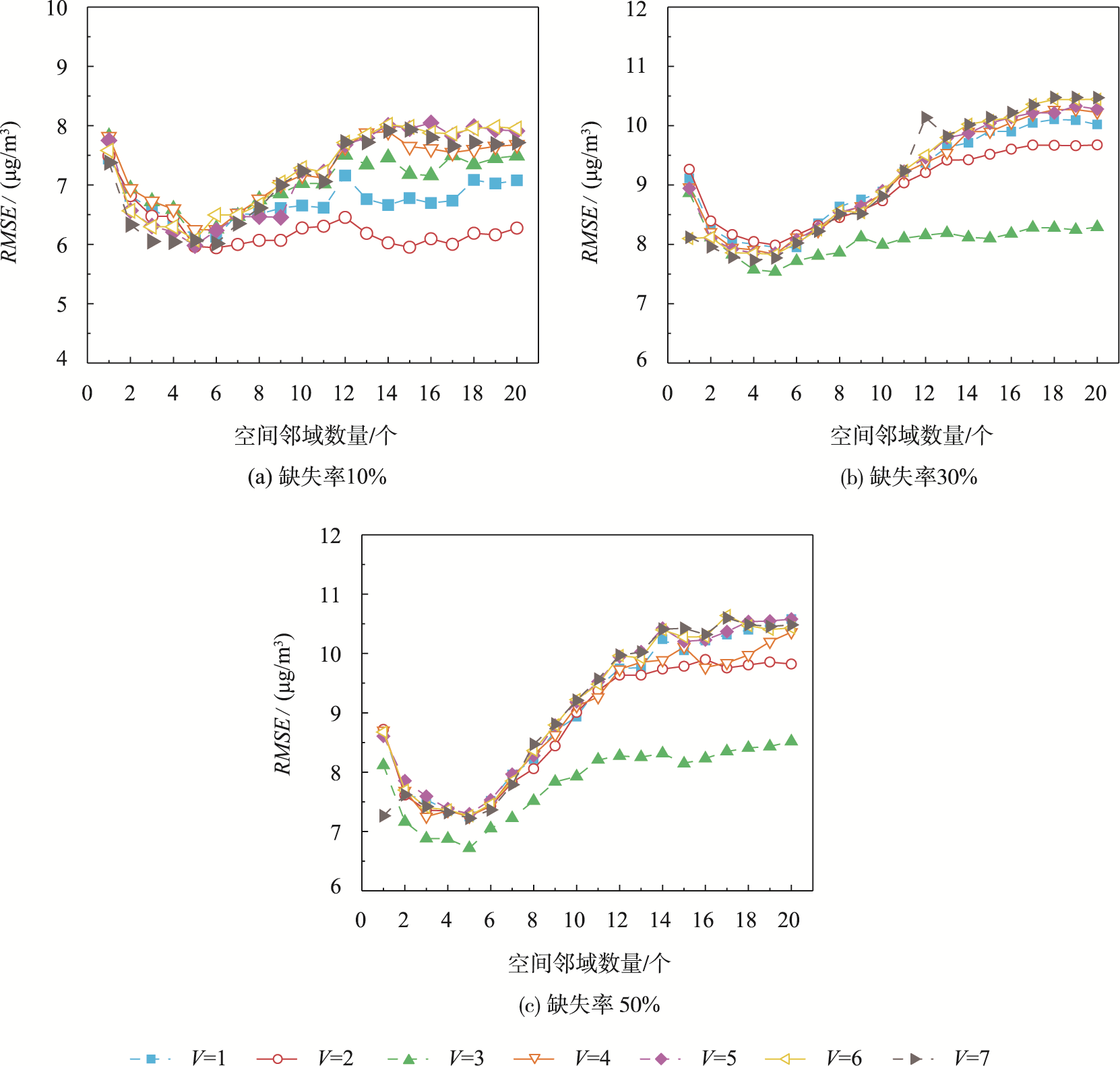
以日周期为处理单元，在空间维度上选择U个相关性最大的站点作为空间邻域，在时间维度上选择缺失位置前后V个时间间隔作为时间邻域。

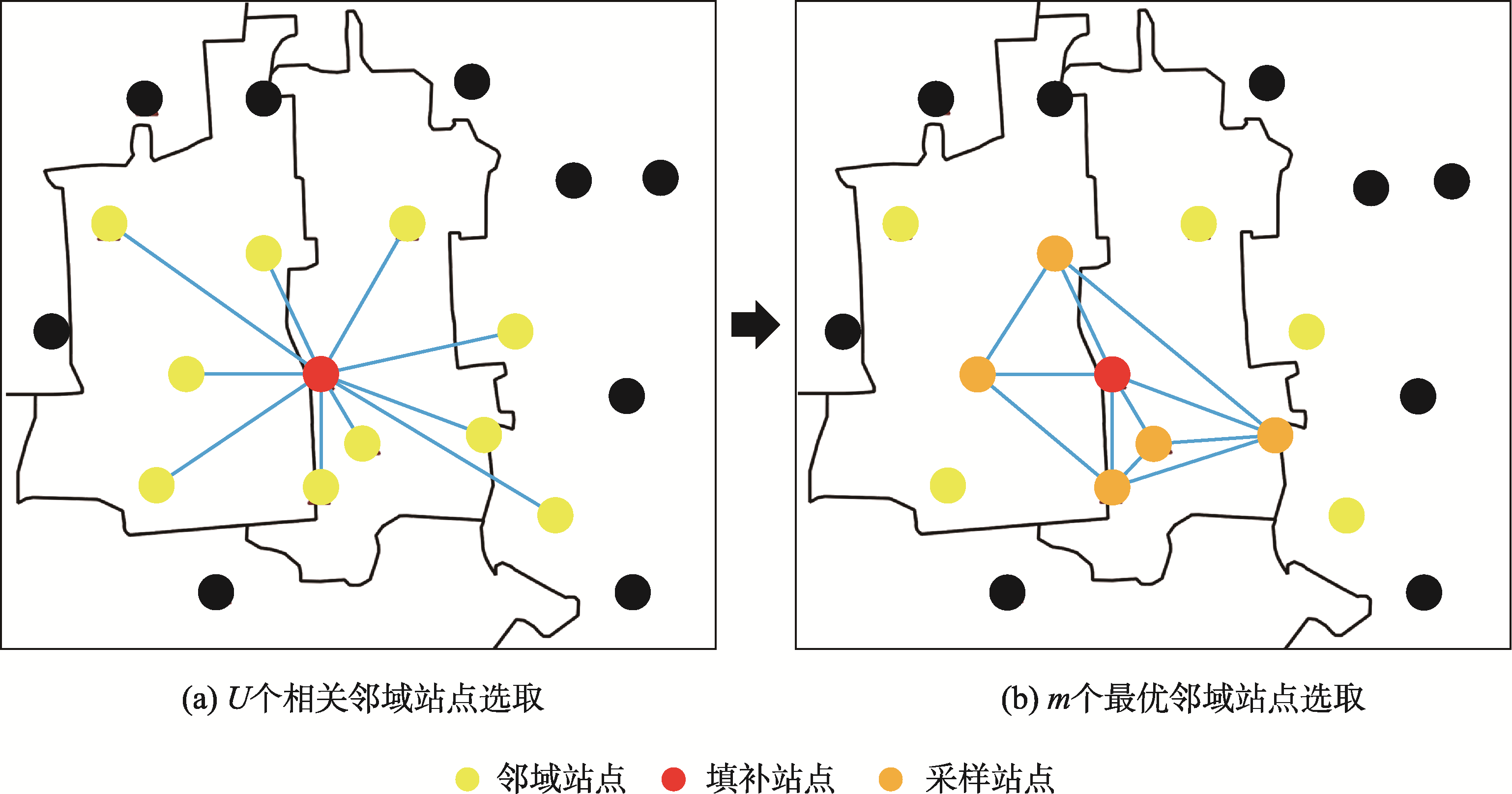
空间最优邻域

图2 缺失值空间最优邻域确定

缺失值初始估计

利用P-BSHADE方法在时间和空间2个维度上重构缺失值，以迭代方式进行空间和时间维度的初始填补，充分顾及时空自相关和时空异质性。

空间维度计算过程：

  1. 计算空间站点关系
  2. 求解空间权重
  3. 计算初始估计结果

缺失值准确填补

在上述时空填补初始值的基础上引入PM2.5影响因子构建Stacking集成学习模型，选择RF、SVM和XGBoost作为基学习器，逻辑回归作为元学习器。

随机森林 SVM XGBoost

方法步骤详解

1. 缺失值最优邻域确定

在空间维度上，从U个初始邻域中选取每天至少包含k个有效值的m个相关性最大的站点作为最优邻域；在时间维度上，选择n个相关性最大且至少包含k个有效值的时间序列作为最优邻域。

2. 缺失值初始估计

对含有缺失值的站点，以该站点缺失值当天的已知观测值的平均值作为其初值；利用P-BSHADE方法对该天站点的PM2.5缺失值进行估算；重复直至所有站点所有天缺失值估算完毕。

3. 缺失值准确填补

将最优时空邻域中全部未缺失位置的空间和时空初始值、PM2.5相关影响因子作为自变量，对应的PM2.5观测值作为因变量输入到Stacking集成模型进行训练；将待计算站点缺失值时刻的空间初始估计值、时间初始估计值、PM2.5相关影响因子作为自变量输入到训练好的Stacking集成模型中，获得最终填补值。

实验设计与结果

实验数据

本文以京津冀站点数据为研究对象，包括气象数据、地理数据等共8项实验数据：

表1 实验数据来源及详细信息

数据类型 名称 来源 分辨率
站点数据 PM2.5 中国环境监测总站(CEMC) 0.01°
气象数据 2 m处空气温度(LST) 欧洲中期天气预报中心(ECMWF) 0.01°
10 m风速(WS) 欧洲中期天气预报中心(ECMWF) 0.01°
相对湿度(RH) 欧洲中期天气预报中心(ECMWF) 0.01°
表面压力(SP) 欧洲中期天气预报中心(ECMWF) 0.01°
露点温度(DT) 欧洲中期天气预报中心(ECMWF) 0.01°
地形数据 高程(DEM) 美国NASA地球数据网站 30 m
土地利用类型(Land-use) 中国科学院空天信息创新研究院 30 m
京津冀PM2.5监测站点分布

图3 京津冀PM2.5监测站点分布

站点缺失情况

日平均缺失率

图4 京津冀PM2.5数据缺失情况

实验结果分析

整体重构精度

表2 各个方法填补结果精度

方法 缺失率 RMSE(μg/m3) MAE(μg/m3)
DP-STF 10% 7.37 4.55
DP-STF 30% 7.53 4.59
DP-STF 50% 7.73 4.69
IST2SMR 10% 8.91 5.26
STPI-BSHADE 10% 12.2 7.54

不同缺失率精度比较

表3 不同缺失率精度及计算时间平均值

方法 RMSE(μg/m3) MAE(μg/m3) R2 计算时间(s)
DP-STF 7.19 4.12 0.968 1,143.36
IST2SMR 12.10 6.88 0.915 523.64
STPI-BSHADE 14.99 8.68 0.875 746.41
ST-SILM 13.77 7.65 0.893 1,578.19
10%缺失率站点R2分布

图5 不同缺失率各站点R2分布

讨论与分析

时空邻域数量分析

不同时空邻域数量比较

图6 不同时空邻域数量比较

随着空间邻域数量(K)的增加，所提出方法的精度呈现出最初的增加，随后的下降。对于时间邻域(D)的比较也是类似的。当缺失率为10%时，U(V)的最佳值为6(2)，而对于其他2个缺失率，U(V)的最佳数值为5(3)。这意味着应该使用更多的时间邻居来估算具有更大缺失率的数据。

时空异质性影响

与基于IDW-SES的方法、S-PBSHADE和T-PBSHADE相比，该方法的平均RMSE(MAE)分别降低了52.0%(44.8%)、21.9%(21.6%)和15.0%(12.3%)。这表明，通过时空耦合插值，重构的PM2.5记录精度得到了显著提高。

研究结论

方法创新

本文提出的DP-STF方法考虑了PM2.5的日周期性变化、PM2.5观测值之间的时空自相关和时空异质性，以及PM2.5与预测因子之间的复杂非线性关系。

精度优势

与7种经典方法相比，本文方法平均RMSE、MAE至少降低了39.83%、40.12%，R2至少提高了5.56%。能够有效捕捉PM2.5极值，极大提升了在时空非平稳区的预测精度。

应用价值

该方法可为空气污染防治、城市环境建设和蓝天保卫战等国家大型环境治理工程提供支持，有助于构建完整的PM2.5浓度数据集。

代码与数据

本文代码已进行公开，所有用户可从以下链接免费获得：

https://github.com/SD-CGG/DP-STF