引言
随着我国城镇化水平的不断提高与发展,空气污染问题在多个领域备受关注。PM2.5是导致中国空气污染的主要原因之一,长期暴露在高浓度的PM2.5环境中会严重危害人体健康,增加患肺癌和心脏病的风险。
目前的PM2.5浓度预测模型方法主要有数值模拟方法、统计建模方法、机器学习方法和深度学习方法。数值模拟方法主要是基于大气污染物形成、扩散、沉降的原理和机制,通过数学或物理的方式构建大气污染物的稀释和扩散等模拟演化模型进行污染物浓度预测。
现有方法在考虑监测站点间PM2.5浓度的空间相关性时,使用欧氏距离将监测站点间的空间相关性建模为各向同性,而使用风向来衡量站点间的空间相关性时,未考虑到山脉或沟谷等地形对站点间PM2.5传输的产生的各向异性影响,影响预测模型的精度和可解释性。
研究方法
2.1 多源变量属性耦合
研究表明,气象属性(如气温、气压、降雨、风速)以及土地利用类型与PM2.5浓度之间存在着显著关联。为了综合考虑影响站点PM2.5浓度的因素,本研究将气象因素中的气温、气压、风速、降雨建模为站点的动态属性(D),将土地利用信息建模为站点的静态属性(L)。
Et = [Xt, L, Dt-m,t1, Dt-m,t2,..., Dt-m,ti], Et ∈ Rn×(2+i×m)
2.2 PM2.5传播距离计算
地理学第一定律指出"一切事物都与其他事物相关,但近距离事物比远距离事物更相关"。考虑到PM2.5污染物在不同监测站点间存在传输与扩散,所以距离越近的监测站点间的空气污染物的浓度特征越具有相似性。然而,山脉等高地形区域会对空气污染物的传播会产生阻隔作用,导致污染物的各向异性传播。
地形距离计算定义
本研究通过计算地形约束下的PM2.5传播路径来近似表征地形对PM2.5空间传输的影响。采用A*算法在DSM数据中计算PM2.5的空间传输路径。
mpq = ∑i=1k Ci
站点风向约束定义
站点间的空气污染物的传输作用会受到风向的影响。为了进一步解决站点间PM2.5浓度相关性的各向异性问题,将风向和地形距离相结合,计算任意时刻站点间的PM2.5传播修正距离。
wij(mij,θij(t)|α = {0, 90°<θij(t)≤180°; e(-mij2×sinθij(t))/2α2, 0°≤θij(t)≤90°}
PM2.5传播路径对比示意图
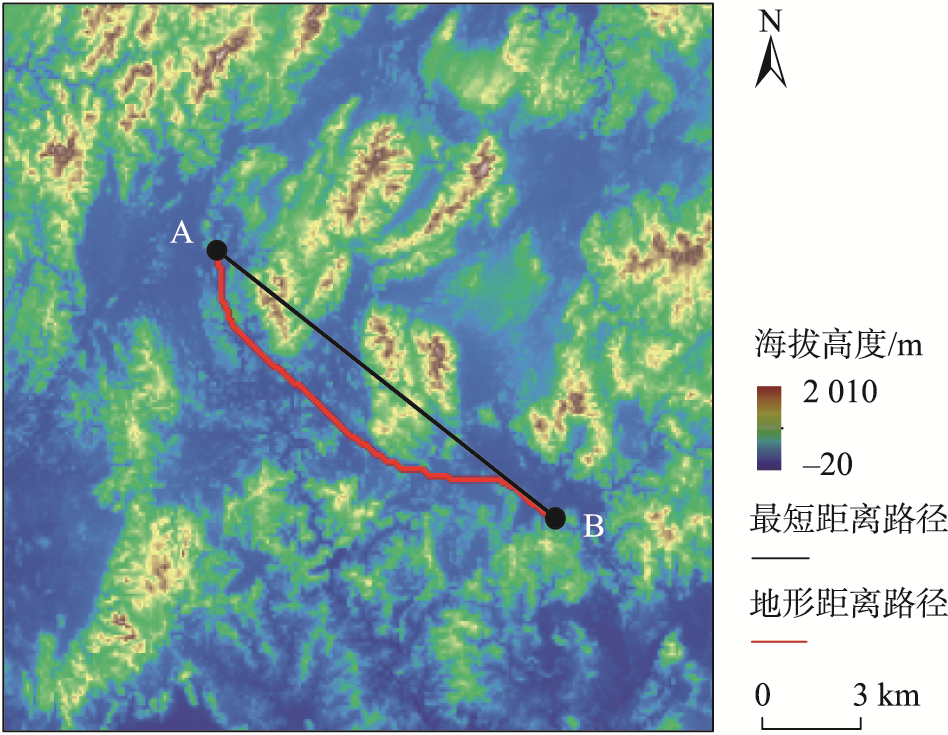
图1 PM2.5传播路径对比示意图
2.3 模型构建与预测
将研究区域内的空气质量监测站点以及站点间的关系看作一个图G=(V, W)。V={v1, v2, ..., vn}表示图中所有的节点的集合,即空气质量监测站点的集合,n是空气质量监测站点的数目,W表示图中节点的边,即站点间的距离。
本文预测模型整体框架
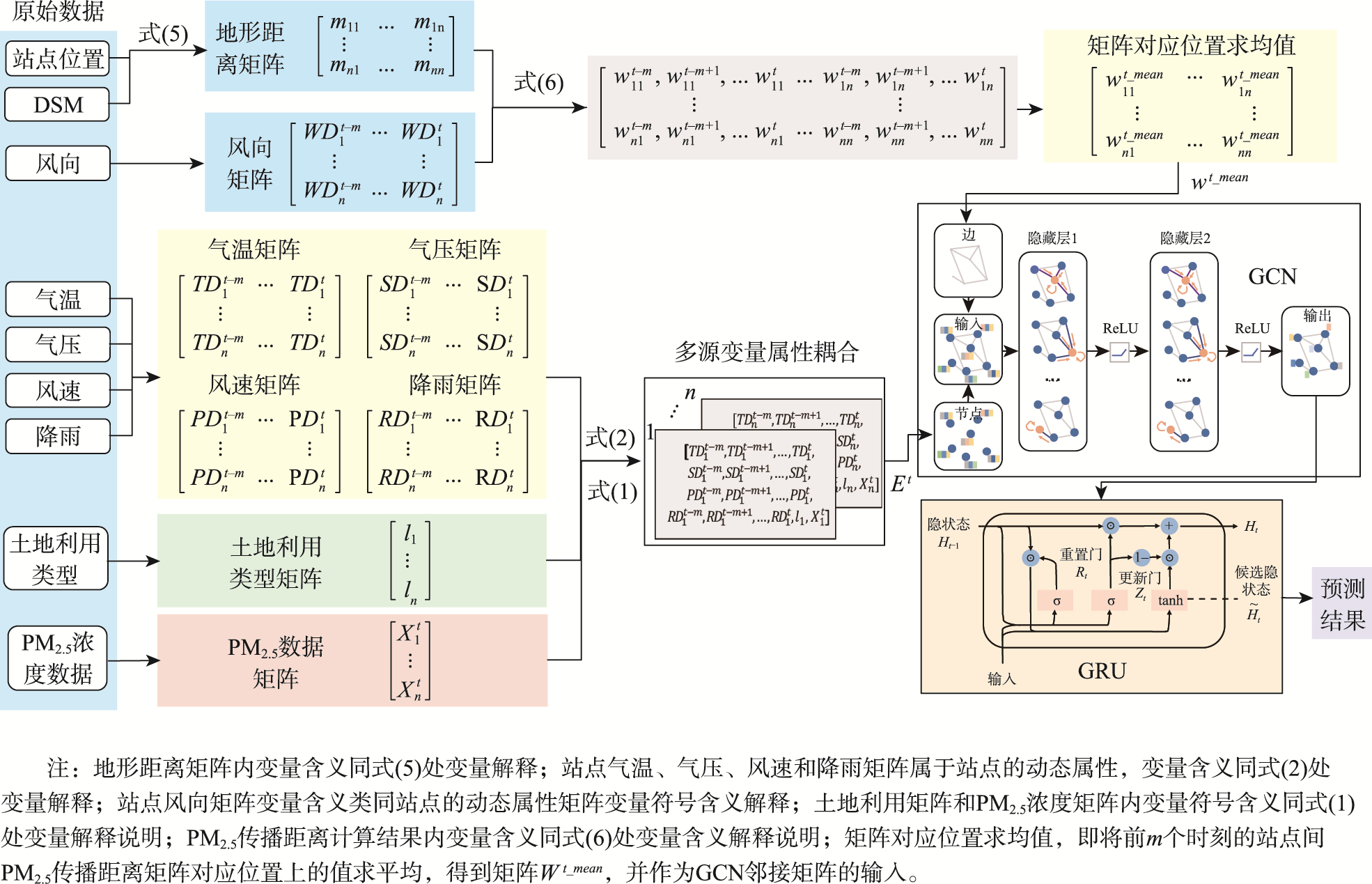
图2 本文预测模型整体框架
实验及结果分析
3.1 实验设计
3.1.1 研究区域与数据集介绍
本文选择位于中国西南地区的贵州省(24°37'N—29°13'N,103°36'E—109°35'E)作为研究区域。贵州省位于云贵高原,地势西高东低,自中部向北、东、南三面倾斜,其中92.5%的面积为山地和丘陵。
贵州省空气质量监测站点空间分布
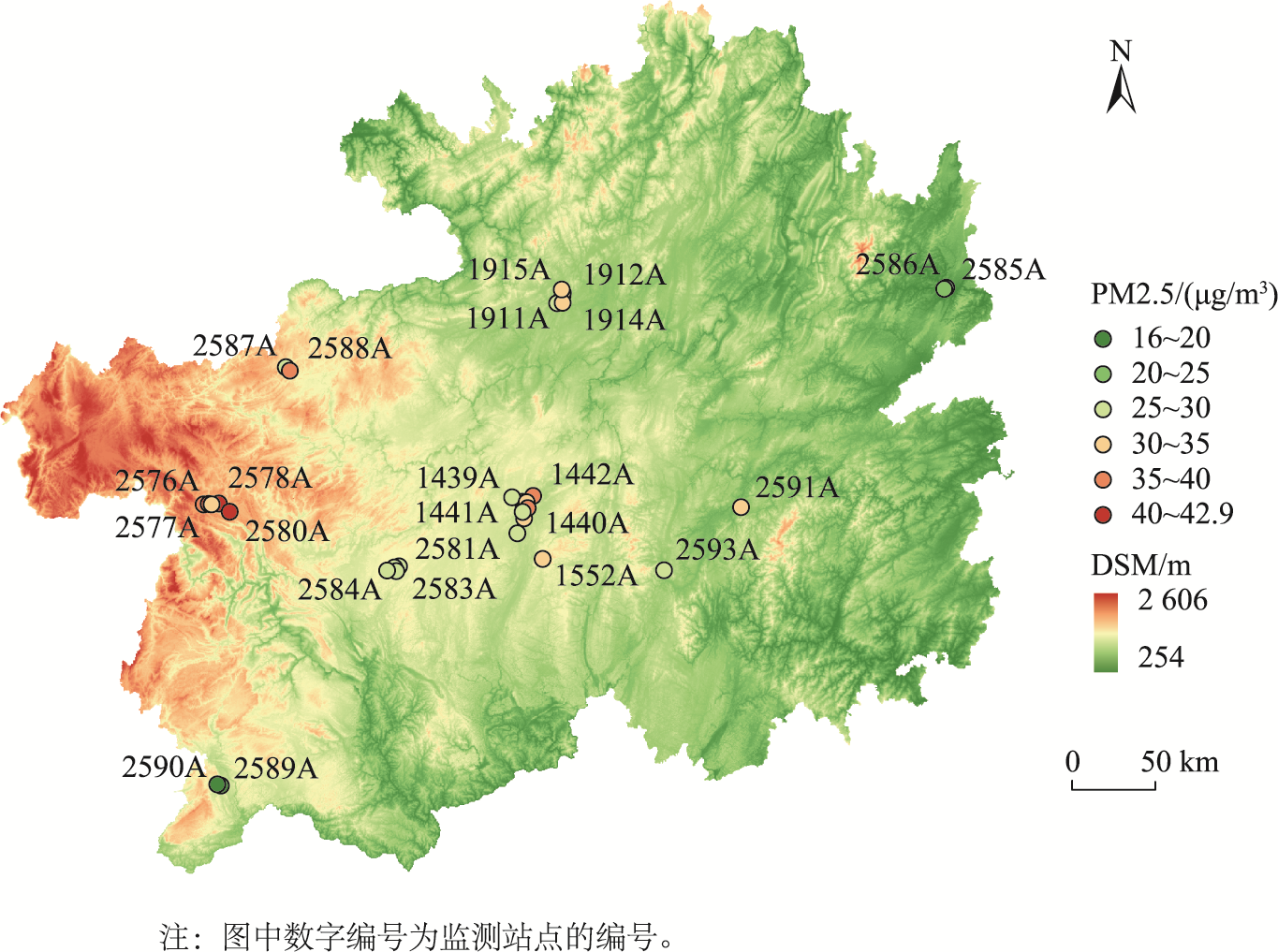
图3 贵州省空气质量监测站点空间分布
表1 本文实验数据及其特征描述
| 数据类型 | 数据来源 | 数据年份 | 取值范围 |
|---|---|---|---|
| PM2.5/(μg/m³) | 中国环境监测总站 | 2017 | [1.00, 863] |
| 气温/°C | ECMWF | 2017 | [-4.26, 39.92] |
| DSM/m | ALOS | 2017 | [254, 2 606] |
3.1.2 实验参数设置及模型评价指标
模型的最大训练次数为2 000次,并采用早停策略(Early Stopping),早停参数设置为10;学习率设置为0.01;Batch Size为128;GCN层数为2;GRU单元数为16;权重衰减率设置为0.000 5;损失函数为平均绝对误差(Mean Absolute Error, MAE);优化器采用自适应矩估计(Adaptive moment estimation, Adam)。
3.2 模型预测结果分析
3.2.1 不同预测模型结果对比
基于贵州省2017年数据集,完成逐小时的PM2.5浓度预测与评估,并与现有时空模型预测结果进行对比来验证所提出模型的性能。
表2 不同方法在测试集上的性能比较
| 方法 | RMSE | MAE | R2 |
|---|---|---|---|
| GTWR | 19.1250 | 15.5995 | 0.6838 |
| STSVR | 14.2656 | 10.3157 | 0.7638 |
| 本文方法 | 10.0466 | 6.8480 | 0.8828 |
3.2.2 不同时间范围模型预测性能
为了评估本文所提模型在不同输入时长(1、2、3、4、5和6 h)和预测时长(1、2、3和4 h)的性能,进行了不同输入时长和预测时长的实验。
不同输入时长和预测时长的RMSE预测结果
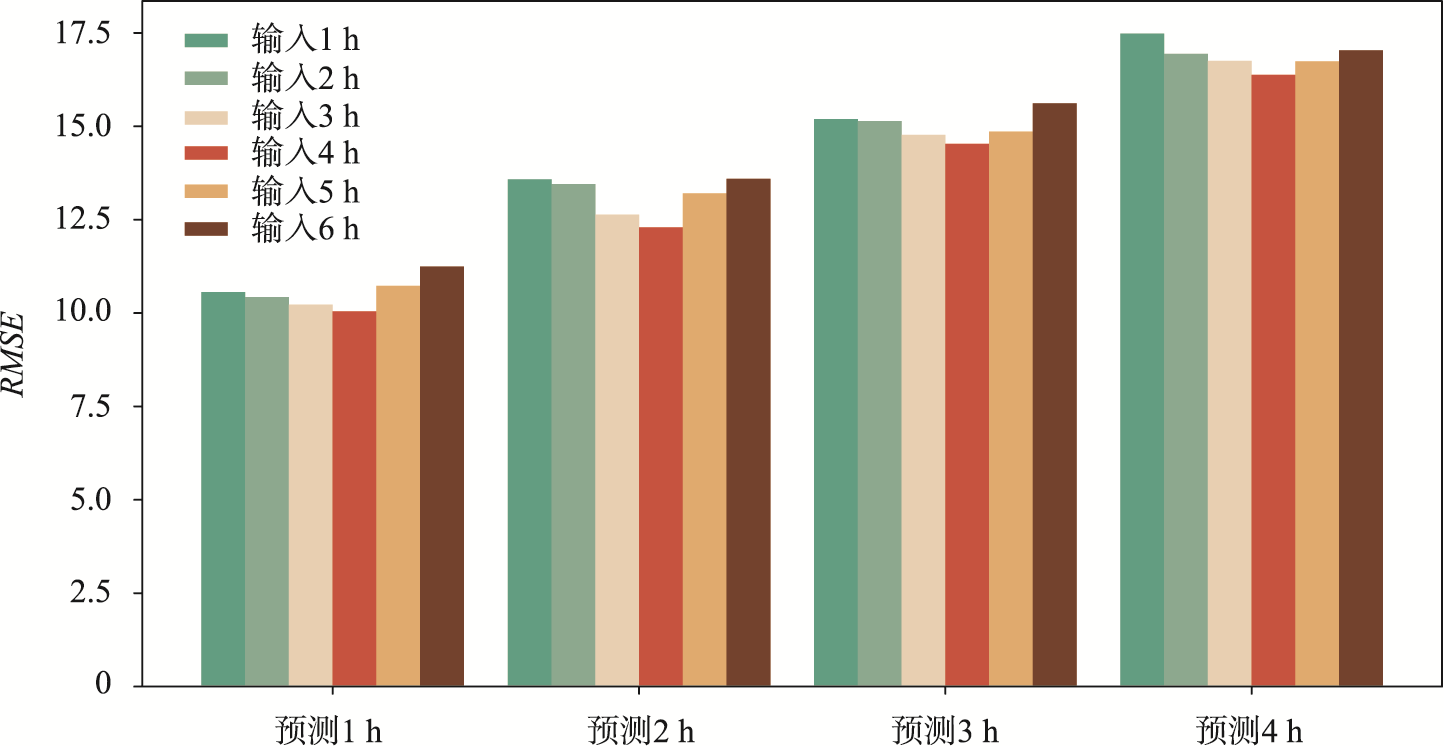
图4 不同输入时长和预测时长的RMSE预测结果
3.2.3 模型预测结果空间化分析
为了体现本研究所提模型对所有站点同时预测结果的优势,随机选取测试集中连续5 h的预测结果与真实结果进行对比,并以克里金插值结果图的形式进行可视化。
本文模型预测结果空间连续插值结果
图5 本文模型预测结果空间连续插值结果
3.3 地形因素影响分析与讨论
地形修正距离与站点PM2.5浓度相关性
在保持风向基本相同时,分析站点间存在与不存在山脉等高地势地形时站点相关性。首先选取3个站点A、站点B、站点C,且站点A与站点B之间存在较高地形阻隔,站点B与站点C之间没有较高地形区域。
地形对PM2.5浓度相关性影响
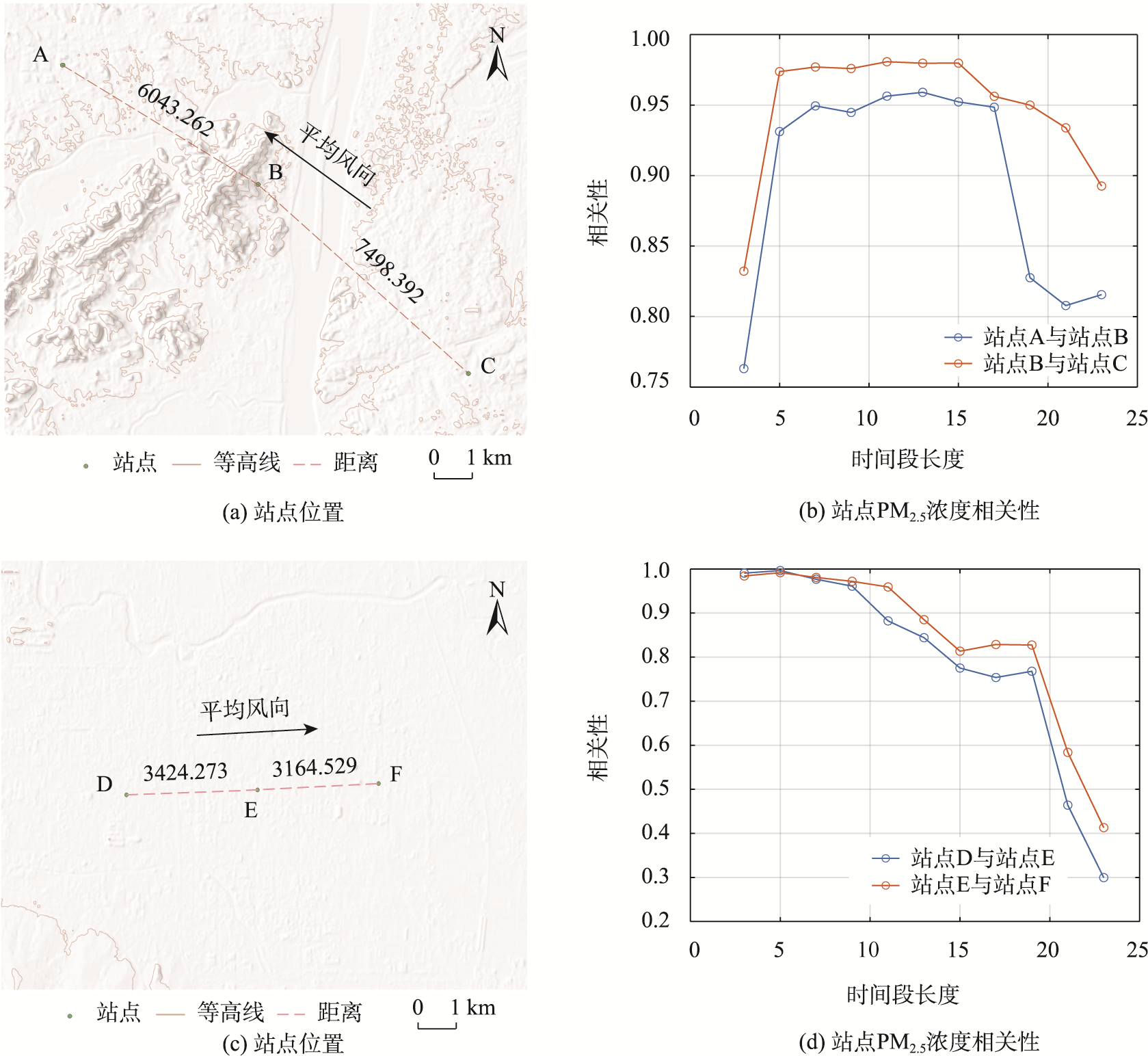
图6 地形对PM2.5浓度相关性影响
地形距离的有效性评估
由于地形距离作用的影响与气象因素的作用大小(风速大小)是紧密相关的,为了进一步说明考虑地形因素的有效性,本文限定气象条件来对地形因素进行讨论。
表3 不同站点PM2.5浓度预测结果RMSE对比分析表
| 站点 | 不利气象条件 | 有利气象条件 |
|---|---|---|
| 1441A | 4% | 22.19% |
| 1914A | 2% | 8.11% |
不同DSM分辨率对模型预测结果分析
DSM是数字地表模型,涵盖了地表建筑物、桥梁和树木等高度。为了分析不同DSM分辨率对模型预测结果的影响,对30 m分辨率DSM数据进行重采样分别得到300、3 000、30 000 m分辨率的DSM数据。
表4 不同分辨率DSM下的模型预测结果
| 不同分辨率/m | RMSE | MAE | R2 |
|---|---|---|---|
| 30 | 10.9000 | 7.3984 | 0.8621 |
| 300 | 11.3902 | 7.6848 | 0.8494 |
3.4 土地利用类型影响分析与讨论
现有研究表明,草地和水体与PM2.5浓度呈现负相关,而建成区等不透水面与PM2.5浓度呈现正相关,且植被相比水体能更有效降低PM2.5浓度。
表5 不同土地利用类型上站点的PM2.5浓度预测结果
| 预测结果 | 1911A(水体) | 2578A(建成区) | 2581A(植被) |
|---|---|---|---|
| RMSE | 9.0761 | 15.6879 | 8.5214 |
| R2 | 0.8842 | 0.8276 | 0.9279 |
结论
为了解决站点间PM2.5传输过程同时受到地形和风向因素的而产生的各向异性影响,引入站点间地形距离并结合风向来建模PM2.5在地形和风向约束下的空间传输过程,进而提出了一种顾及地理环境各向异性的PM2.5浓度时空图卷积网络预测模型。
以地形距离和风向来衡量站点PM2.5传输扩散的各向异性,并结合站点的其它气象因素和土地利用类型特征,采用GCN模型计算空间特征,并通过GRU建模PM2.5浓度的时间序列特征,构建顾及地理环境各向异性的时空图卷积网络预测模型,为PM2.5浓度的精准预测提供了一种新的思路。
通过在中国贵州省的PM2.5浓度预测实验表明,地理环境中各向异性的因素(地形、风向)对PM2.5浓度预测效果具有重要影响。本文顾及地形距离和风向改进的预测模型相比于现有方法在不同地形均能有效降低站点PM2.5浓度预测误差,尤其是在沟谷地形本文方法相比于最优对比模型的RMSE降低约为22%,有效提升了PM2.5浓度预测的精度,对空气污染预测和防治具有重要参考价值。
本文研究仍然存在一些局限性。如在考虑PM2.5的空间传输时,本文主要从自然地理环境特征角度出发考虑了地形因素、气象因素的影响。由于大范围人类活动数据获取较困难,因此本文对于人类活动对于PM2.5传播的影响未进行建模,而人类活动也是影响PM2.5聚集与传播的一个重要因素。因此,需要进一步探索其他因素(如人类活动特征)的影响以提高PM2.5浓度预测精度。