基于边折叠的实景三维模型简化算法

1 引言

实景三维是对一定范围内人类生产、生活和生态空间构建真实、立体、时序化反映和表达的数字空间。实景三维模型是实景三维中国建设中的数据底座，当前的实景三维模型一般采用倾斜摄影采集技术、LiDAR激光雷达扫描技术、人工建模技术等方法创建接近实际场景的三维模型。

然而，实景三维模型具有结构复杂、数据量大等特点，给数据存储、处理和渲染都带来了巨大的挑战。为确保在复杂网络环境下，实景三维模型数据在三维可视化场景中进行复杂而高效的可视化与分析任务，对于满足不同应用需求的可视化效率与效果进行优化的研究也日渐丰富。

在现有计算机硬件的条件下如何渲染大数据体量的实景三维建筑模型来保证三维可视化的效率与效果是最关键的问题。因此，对实景三维模型进行简化变得尤为必要。

实景三维模型通过简化，可以降低模型的复杂度，在保持模型主要形状和特征的同时，消除冗余的几何信息，使得实景三维模型更加轻量化，以达到减少模型数据量和提高渲染效率的目标。

目前，被国内国外广泛采纳的三维模型简化技术主要涵盖几何删除法和顶点重采样法等多种方法。在这些技术中，顶点重采样法存在一些弊端，比如多次对模型进行采样可能引起失真，造成视觉效果较差，而且实现的难度较大。

相较之下，几何删除法因其清晰的思路、对计算机硬件要求相对较低以及简化后模型能够保持良好视觉效果等诸多优势，已经成为广泛应用的简化技术。几何删除法根据删除元素的不同，可分为顶点删除法、边折叠法、三角面片塌陷法等多种方法。

在这些方法中，边折叠法因其简化速度快、效率高，同时还能维持原模型的拓扑结构，因此成为目前应用最广泛的简化技术之一。

2 研究方法

如图1所示，本文研究方法包括数据预处理、QEM算法描述、基于QEM的边折叠简化改进算法、拉普来是网格优化处理4个重要过程。

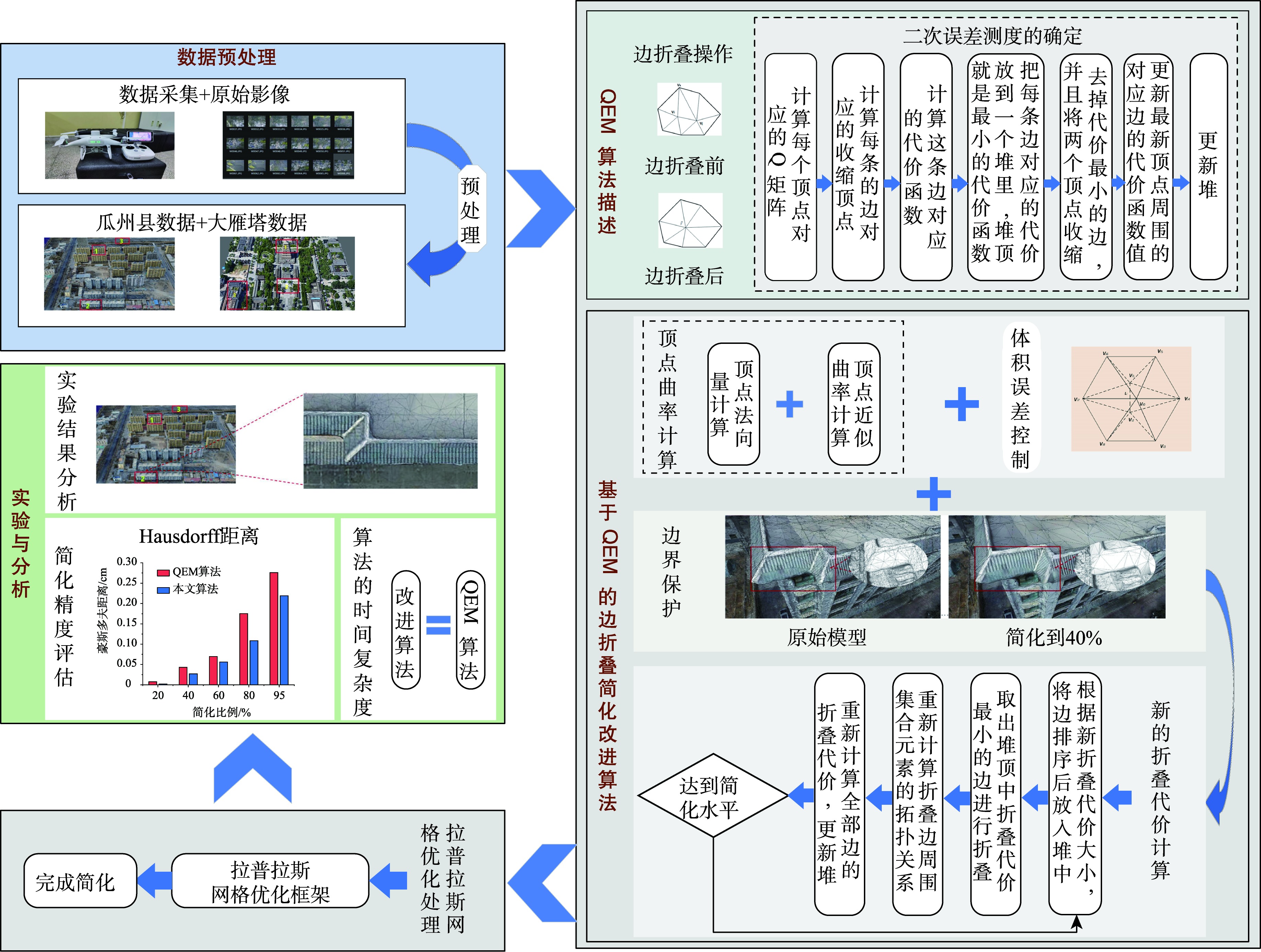
图1 技术流程

在网格简化的过程中，每次都选择具有最小折叠代价的边进行折叠操作。目前，通常通过逐一搜索和对比的方式来寻找具有最小折叠代价的边。然而，一种更加精细的方法是利用二叉堆来存储边的折叠误差队列，并借助堆排序的原理将边的折叠代价进行排序，使得每次迭代简化时，更易于提取具有最小折叠代价的边。

考虑到实景三维模型在不同区域有不同的细节特征保持需求，本文在折叠代价中引入顶点曲率及体积误差控制，以实现更为灵活的简化操作。

2.1 数据预处理

本文采用无人机航拍得到甘肃省酒泉市瓜州县倾斜摄影影像数据，然后使用smart3D对采集数据进行内业处理，内业处理包括空三测量、构建TIN模型（三角网模型）等过程。在本文中，smart3D软件处理后输出OSGB格式的Mesh模型。

2.2 QEM算法描述

2.2.1 边折叠操作

边折叠算法是Hoppe最早提出的一种三角网格方法，该算法通过不断迭代进行边折叠操作达到简化的目的。迭代进行边折叠过程中，每次选择折叠误差最小的边，删除与该边所有相邻的顶点与面，然后对边折叠后所产生的空洞重新进行三角化。

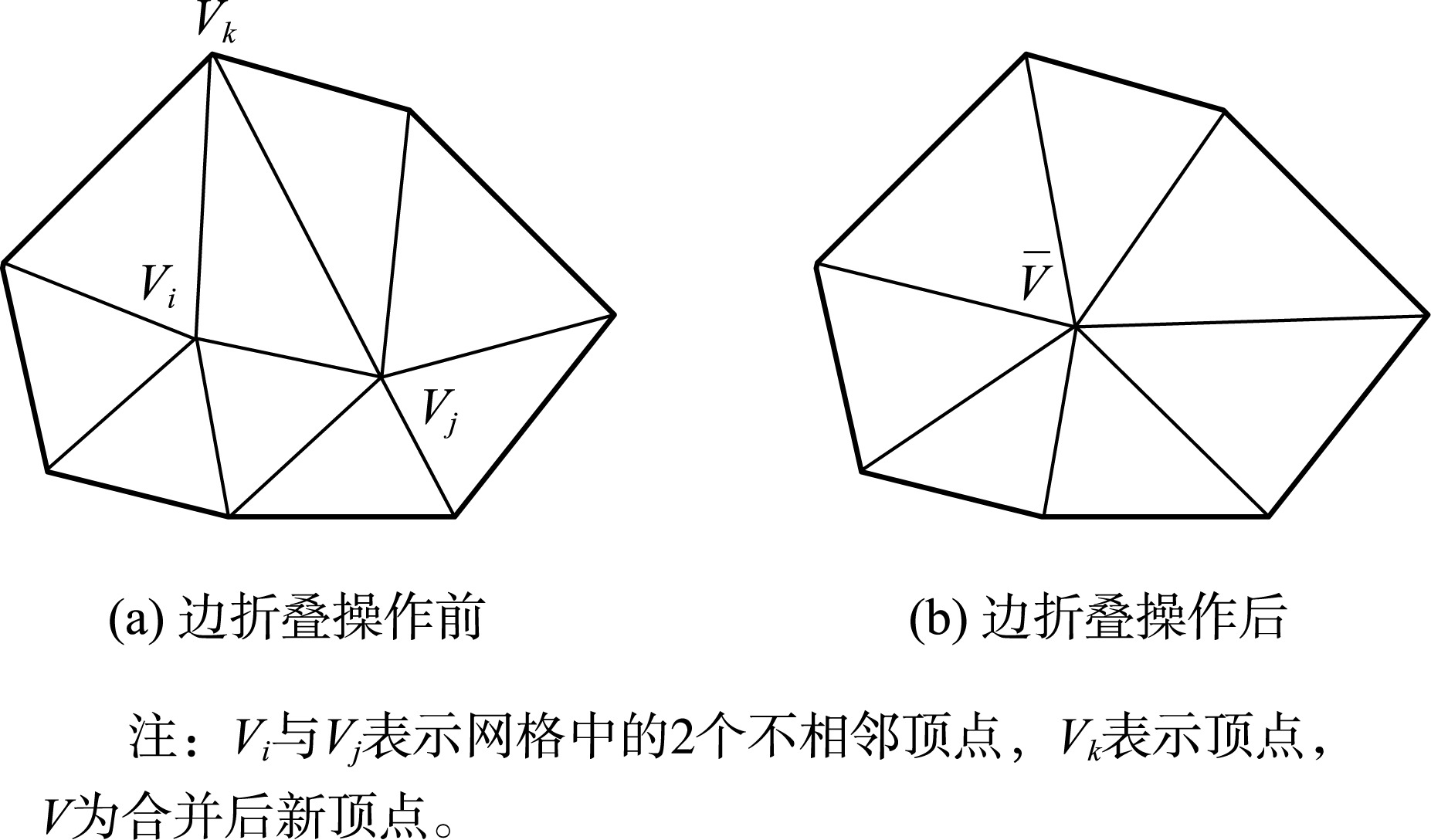
图2 边折叠算法

2.2.2 二次误差测度的确定

一条边是否需要折叠是由其折叠代价决定的，本文使用二次误差测度（QEM）来计算折叠边的代价。定义网格中顶点V=[V_x V_y V_z 1]^T，所有初始误差矩阵为Q。

2.3 基于QEM的边折叠简化改进算法

2.3.1 顶点曲率计算

在微分曲面中，曲率是一种用于量化曲面细节特征信息的度量指标，它能够描述曲面上折痕、拐点和尖角等特征变化明显的区域。由于三维模型由众多三角网格构成，通常使用网格顶点的离散曲率来衡量顶点位置的凹凸程度。

2.3.2 体积误差控制

在对一些细节要求较高的实景三维模型中，仅仅依靠顶点近似曲率无法充分捕捉局部细节特征。为了更准确地度量模型表面的细节特征，本文引入体积误差控制，以确保模型的细节特征区域在简化过程中得到有效保留。

2.3.3 边界保护

在很多情况下，保持模型的边界形状至关重要，特别是对于边界具有特殊语义和功能的模型，如建筑物、汽车等。使用QEM算法简化后模型出现以下结构，如图5所示。

2.4 拉普拉斯网格优化处理

三角形的形状对曲率的影响远比三角形的大小对曲率的影响更加显著。经本文改进简化算法处理后的模型保留了更多细节特征，但仍然存在一些狭长三角形，因此有必要对简化后的网格进行优化处理。

3 实验与分析

本文在硬件配置为2.20 GHz的Intel(R) Xeon(R) Silver 4214 CPU和16 GB内存的环境下，采用C++语言，结合OSG（OpenSceneGraph）、OpenMesh库以及MeshLab工具，实现了改进的QEM算法。

本文使用的场景模型数据源为甘肃省酒泉市瓜州县城区（部分）和陕西省西安市大雁塔通过倾斜摄影测量方式采集航摄影像，经过三维重建技术得到的实景三维模型，然后进行简化实验。在相同简化程度下，对比分析了本文改进算法与传统QEM算法的简化结果，以验证本文方法的有效性和可行性。

3.1 实验结果分析

本文选取2组实验数据各3个典型实验区，如图3所示，包括建筑物和道路，它们通常在地图制作、城市规划、导航和地理信息系统（GIS）中起到关键作用。

图3 实验数据

采用改进算法和QEM算法分别对3个实验区进行40%和80%程度的模型简化，结果如表1所示。

表1 瓜州县模型简化统计

对比项	面片数/个	简化程度/%	本文算法	QEM算法
区域1	209 041	40	69 680	167 232
区域1	181 429	80	60 476	145 143
区域2	92 329	40	30 776	73 863
区域2	526 355	80	175 452	421 085

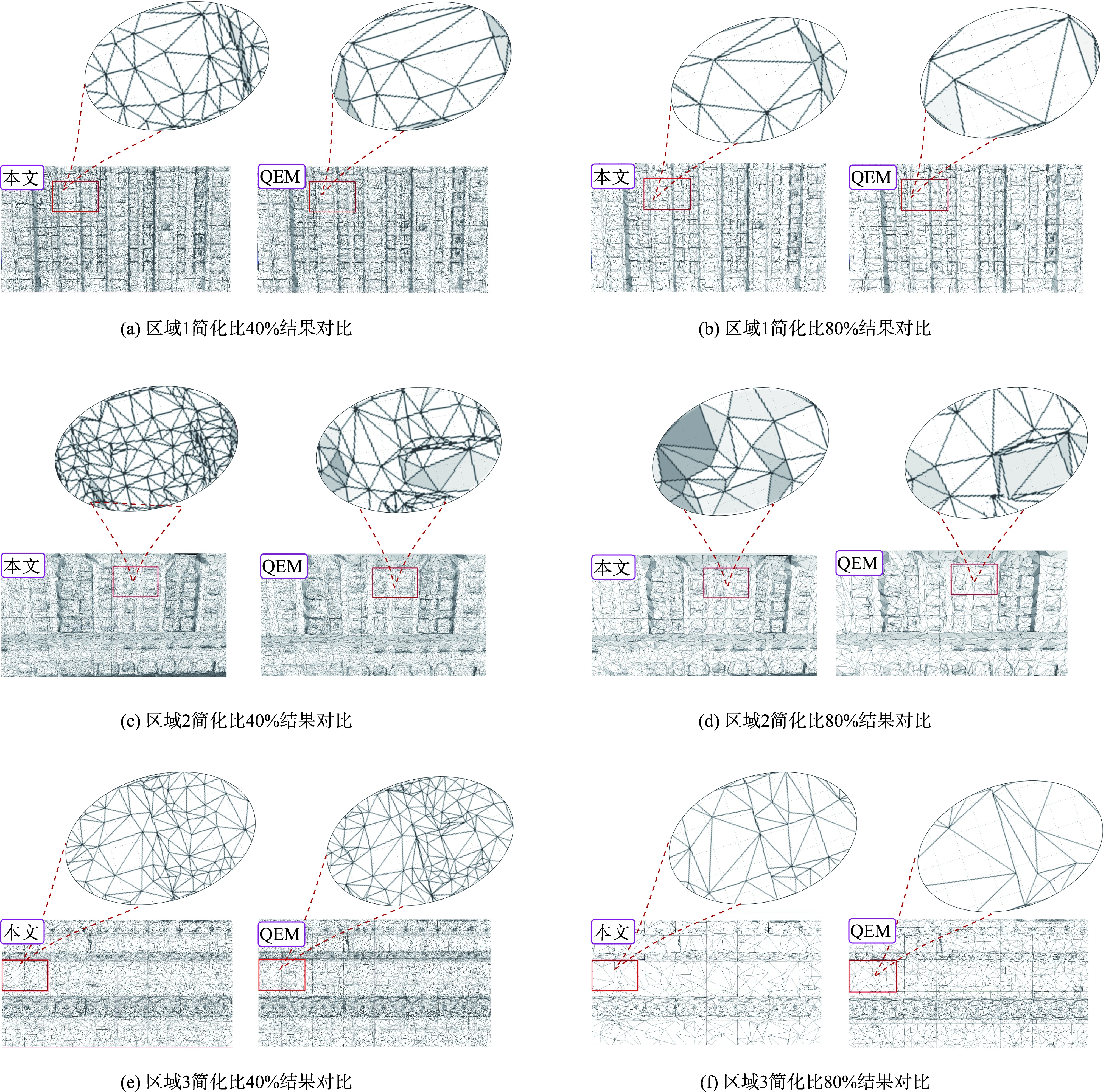
图4 瓜州县数据本文算法与QEM算法简化后效果

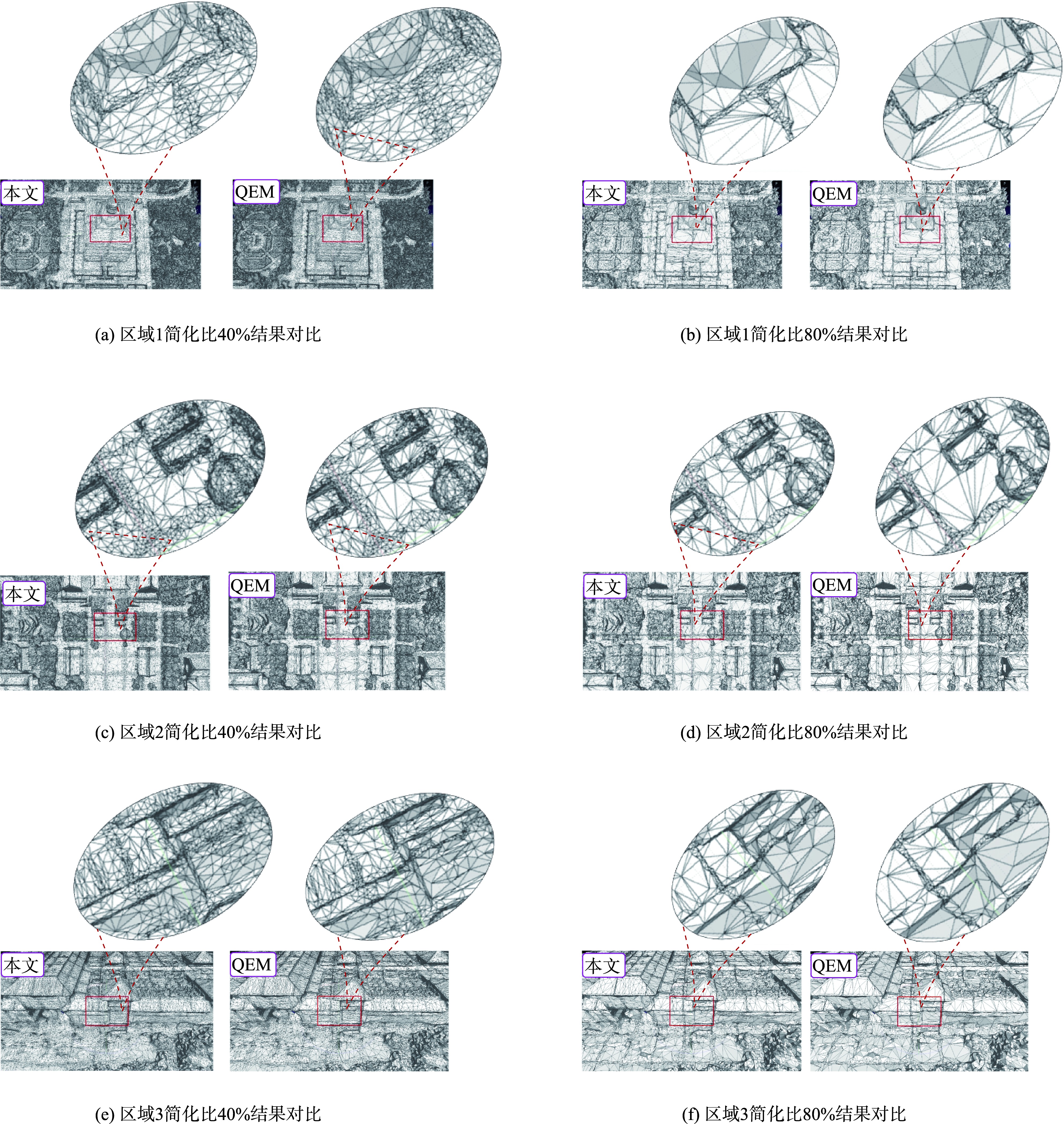
图5 大雁塔数据本文算法与QEM算法简化后效果

3.2 简化精度评估

本文使用Hausdorff距离来量化简化后的模型与原始模型之间的差异，在简化实景三维模型的情境中，Hausdorff距离可以用来评价简化前后模型之间的形状差异，即简化效果。

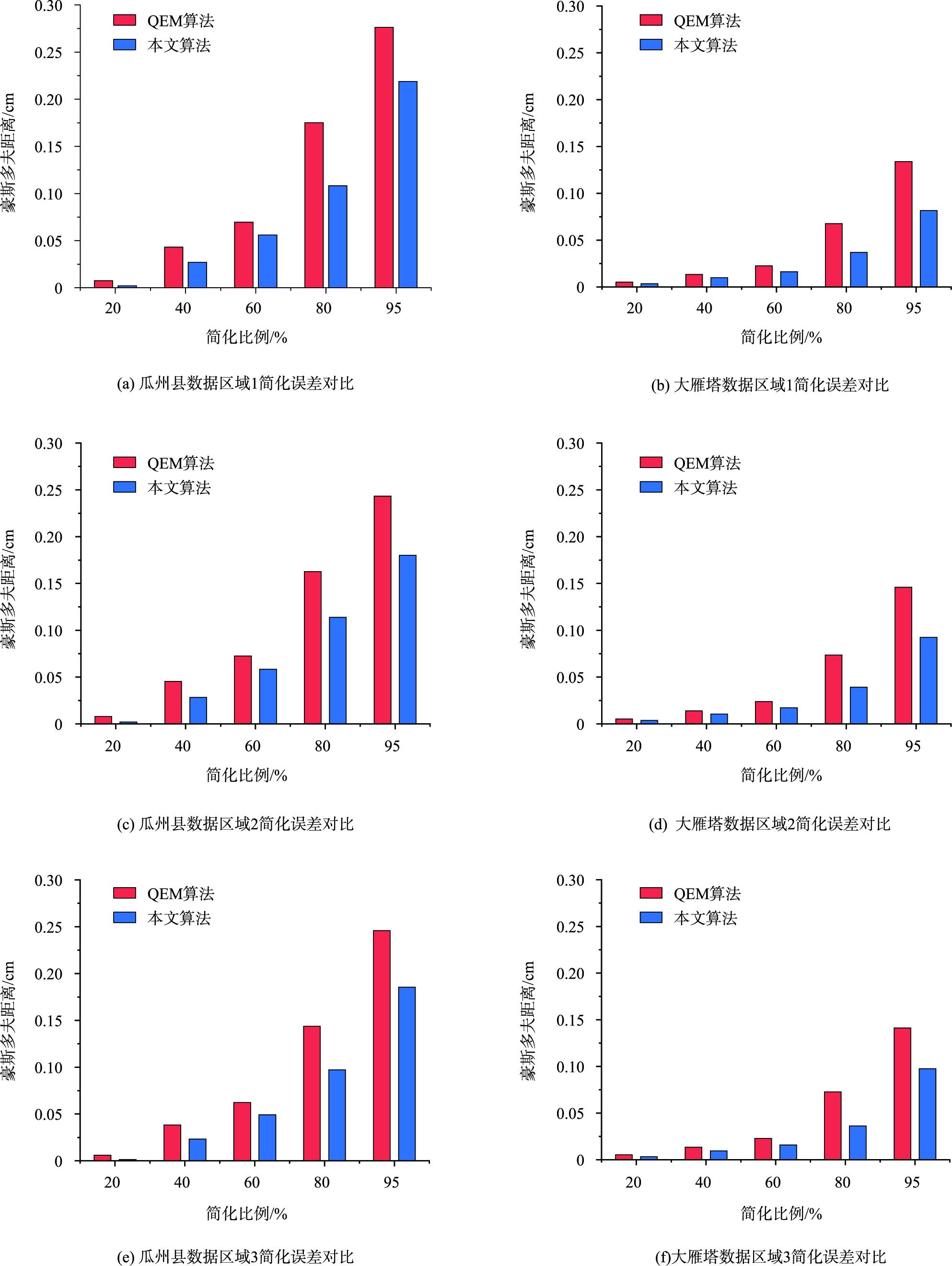
图6 两组数据不同区域简化误差对比

4 结论

实景三维模型作为当前智慧城市、数字孪生以及实景三维中国建设等多个领域的基座，凸显出其在地理信息领域的重要作用。在构建实景三维模型时，需要构建海量的三角网格和纹理，随着实景三维模型数据的真实性以及精确度增强，数据量也在不断的攀升，对计算机性能要求也越高。

虽然目前已有研究也在保留细节及网格质量上有了一些研究成果，但难以在保留细节特征和网格质量之间取得平衡。因此，本文提出一种基于边折叠实景三维模型简化算法。首先基于QEM边折叠算法，通过将顶点曲率和体积误差控制与简化时的边折叠代价结合实现模型简化。

实验结果表明，随着简化程度的不断提高，当简化程度达到80%时，在细节丰富的窗户等区域，本文算法生成的网格数量明显多于QEM算法，且在细节丰富的区域网格越密集。同时，随着简化程度提高本文简化误差相较于QEM算法更低。

但是，本文方法较为耗时，因此下一步将探索利用GPU技术提升方法的性能，使之更加适用于实景三维数据的处理。

* 以上内容由AI自动生成，内容仅供参考。对于因使用本网站以上内容产生的相关后果，本网站不承担任何商业和法律责任。