研究方法
2.1 技术路线
本文旨在结合网眼结构和路网路段结构的优势,以实现路网和网眼群组模式的识别。由于城市路网中格网型、不规则型路网以及直线型、格网型网眼群组最为常见,因此本文选取以上常见的路网模式进行识别。
算法流程包含道路网数据预处理、路网结构构建、特征参量计算、阈值设定与模式分类等步骤。
算法流程
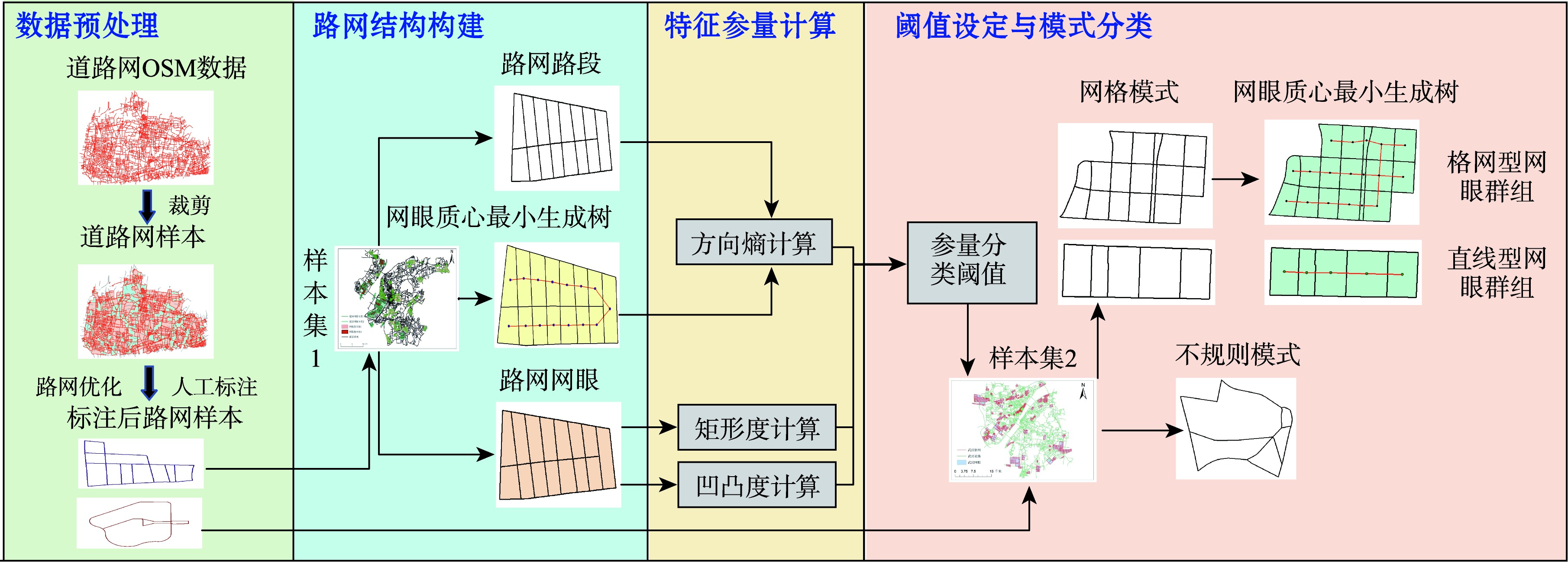
图1 融合路段和网眼的路网模式识别算法流程
2.2 数据预处理
由于OpenStreetMap下载的道路网原始数据内部不仅包含了城市主干道路网,还包含了许多琐碎道路,诸如人行道和自行车道等。同时,道路网自身具有一定的曲线性,因此在实验开始前,先对道路网进行数据预处理:
数据优化过程
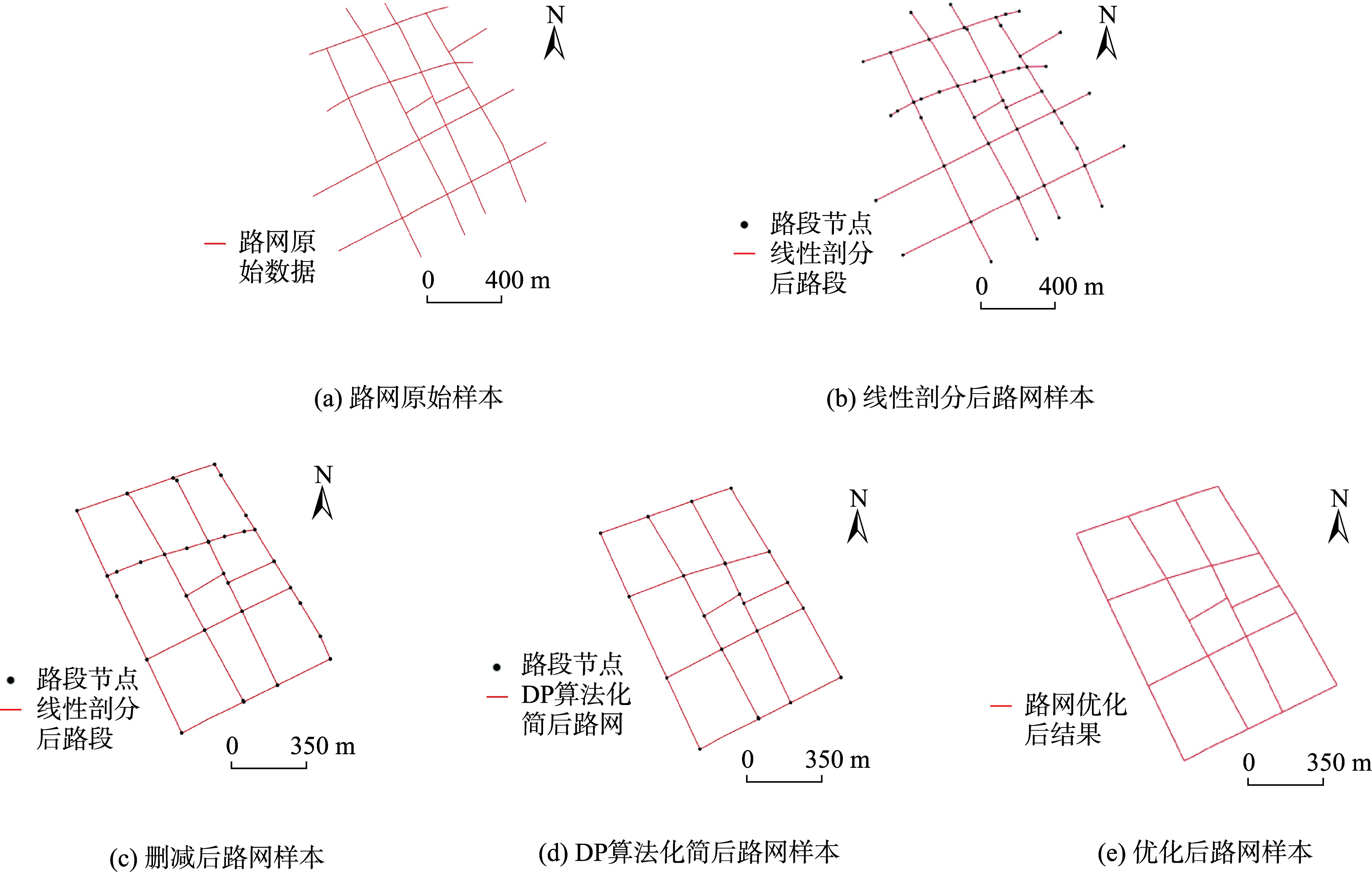
图2 道路网样本集数据优化过程
- 将路网数据按照交叉点分割为多条路段
- 遍历整个道路网,将所有包含节点度为1的首尾节点的路段进行删除
- 遍历删减后的道路网,利用Douglas-Peucker算法对每条路段进行化简
- 优化结束
2.3 网眼最小生成树构建
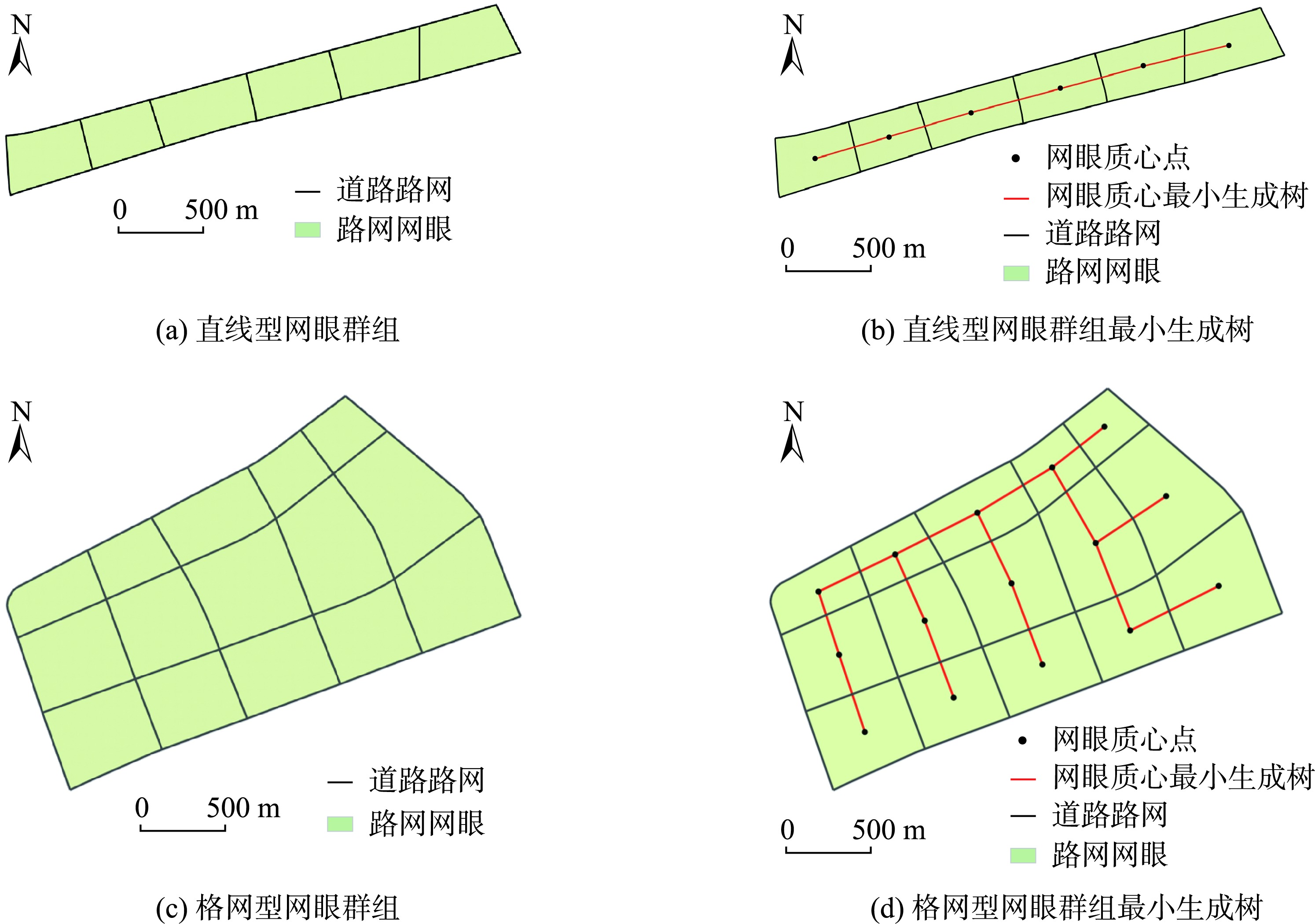
图3 直线型和格网型网眼群组及其最小生成树
根据不同的路网模式,路网所包含的网眼群组的空间分布模式也不尽相同,其中格网路网的直线模式和网格模式是最常见的网眼群组的2种分布模式。
最小生成树(Minimal Spanning Tree)是将N个顶点通过N-1条边连接而成的权值最小无闭合连通子图。对于道路网眼模式识别而言,对网眼群组构建最小生成树具有以下优势:
- 将相邻的道路网眼相互连接起来,方便聚类描述
- 通过构建网眼最小生成树可以较为直观地得出网眼群组的排列方式
- 通过构建网眼最小生成树将网眼群组原本的面状结构转换为边-节点结构
2.4 特征参量计算
分别构建路网的路段结构、网眼结构和网眼最小生成树,并根据结构的不同提取对应的特征参量。其优势在于通过网眼结构可以顾及到每一个网眼的规整情况,通过路段结构和网眼最小生成树结构能够顾及到路网的整体排列方式。
2.4.1 针对网眼的特征参量提取与计算
矩形度 (Rectangularity)
矩形度是指物体外形与矩形外形的相似程度,用于描述一个物体的形状规则程度。在路网中,矩形度通常是指道路网眼面积和网眼最小外接矩形面积的比值,取值范围为(0,1]。
凹凸度 (Convexity)
凹凸度是一种描述多边形凹凸程度的特征参量,也用于描述事物趋近于四边形的程度。在道路网中,凹凸度通常是指道路网网眼面积与网眼所形成的凸壳面积的比值,比值取值范围为(0,1]。
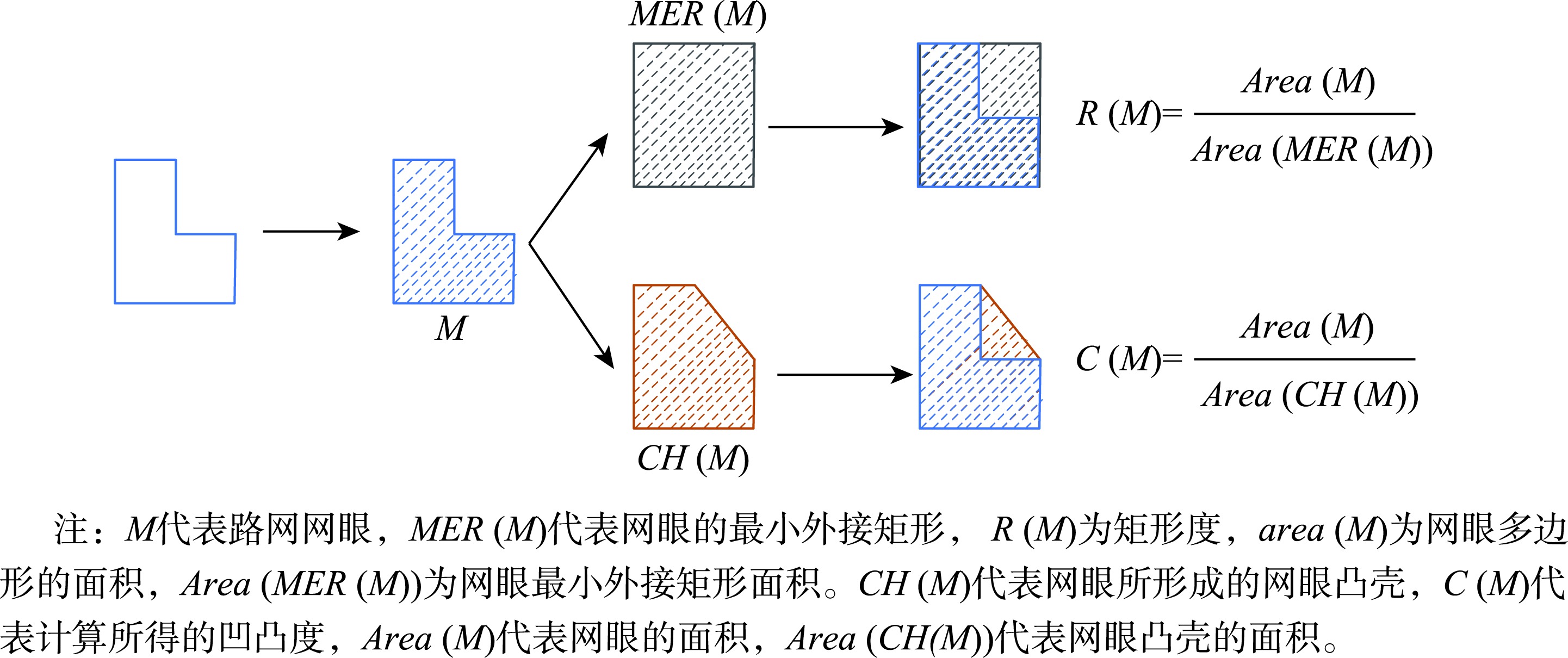
图4 路网网眼特征参量计算
2.4.2 针对边-节点结构的特征参量计算
从路段结构来看,不规则路网和格网路网最明显的区别在于,格网路网的路段排列规整,整体路网具有明显的方向性;而不规则路网的路段排列混乱,路网中路段方向不一致。
本文引入方向熵作为边-节点结构特征参量,借助其在描述数据空间```html 空间分布方面的优势,对路网模式进行快速划分。
方向熵 (Directional Entropy)
方向熵是一种用来反映数据方向分布情况的熵值。假设在空间中存在n个数据点,在使用经纬度或是xyz坐标表示这些空间点的方位时,若发现这些点呈现出特定的分布方向,则可以用方向熵来定量化描述这种方向性。
计算公式:
其中:
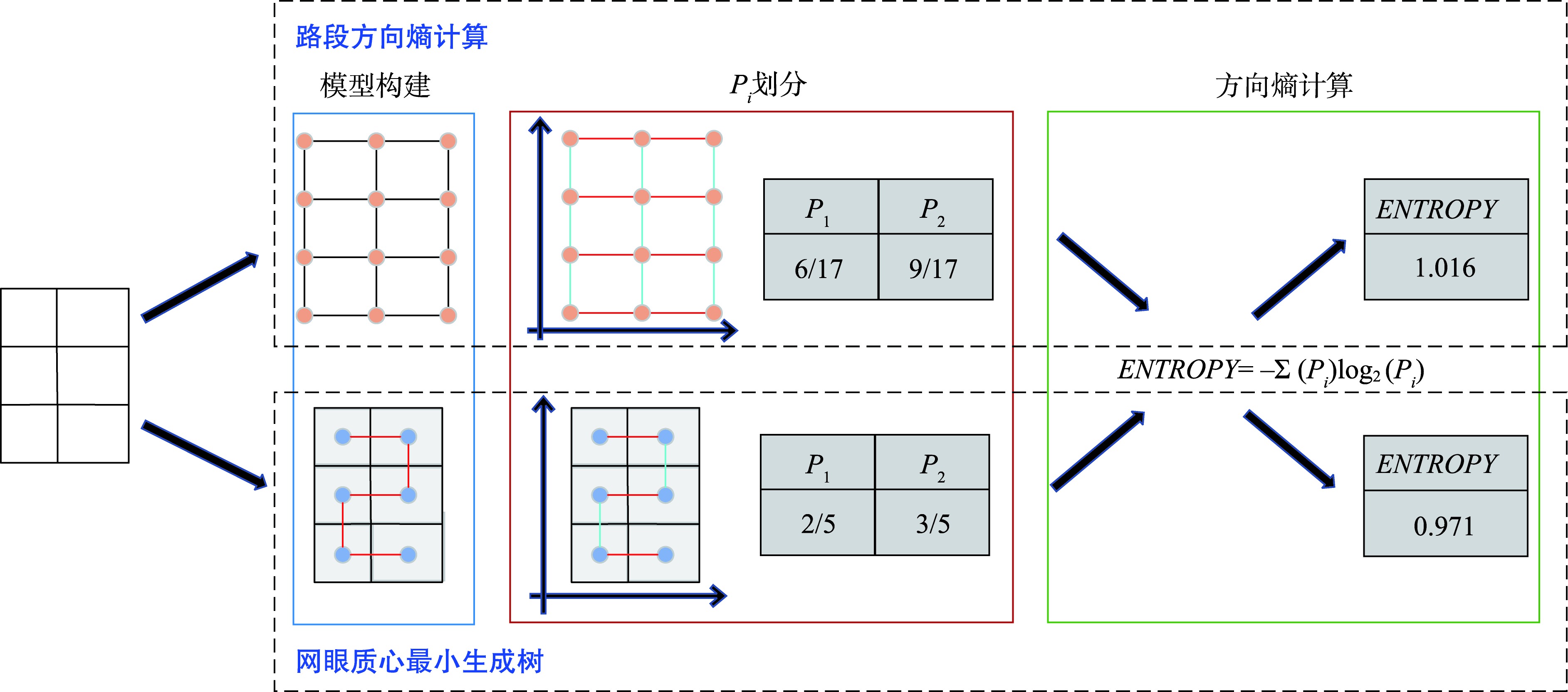
图5 方向熵计算流程
2.5 道路网模式识别
在道路网的模式识别中,矩形度和凹凸度可用来描述路网中每一个网眼的规整情况,方向熵则可以用来描述路网中每条路段以及网眼质心最小生成树每条边的朝向和空间分布规律。
格网路网特征
- 方向熵值一般小于0.25
- 网眼矩形度大于0.75且凹凸度大于0.9
- 路段方向集中在2个方向上
不规则路网特征
- 方向熵值大于2.5
- 网眼矩形度小于0.75或凹凸度小于0.9
- 路段方向分布复杂
网眼群组模式识别
直线型网眼群组
- 网眼沿着一条明显的直线排列
- 网眼最小生成树呈现为一条直线
- 方向熵值为0
格网型网眼群组
- 网眼按照相对固定的方向排列
- 网眼最小生成树由多条直线构成
- 方向熵值在0~2.5之间
实验结果与分析
3.1 参量阈值设定
为完成特征参量阈值统计,本次实验从优化后的南京市和西安市路网中选取出300个网格模式路网和50个不规则模式路网,并将网格模式路网进一步细分为150个直线型网眼群组和150个格网型网眼群组。
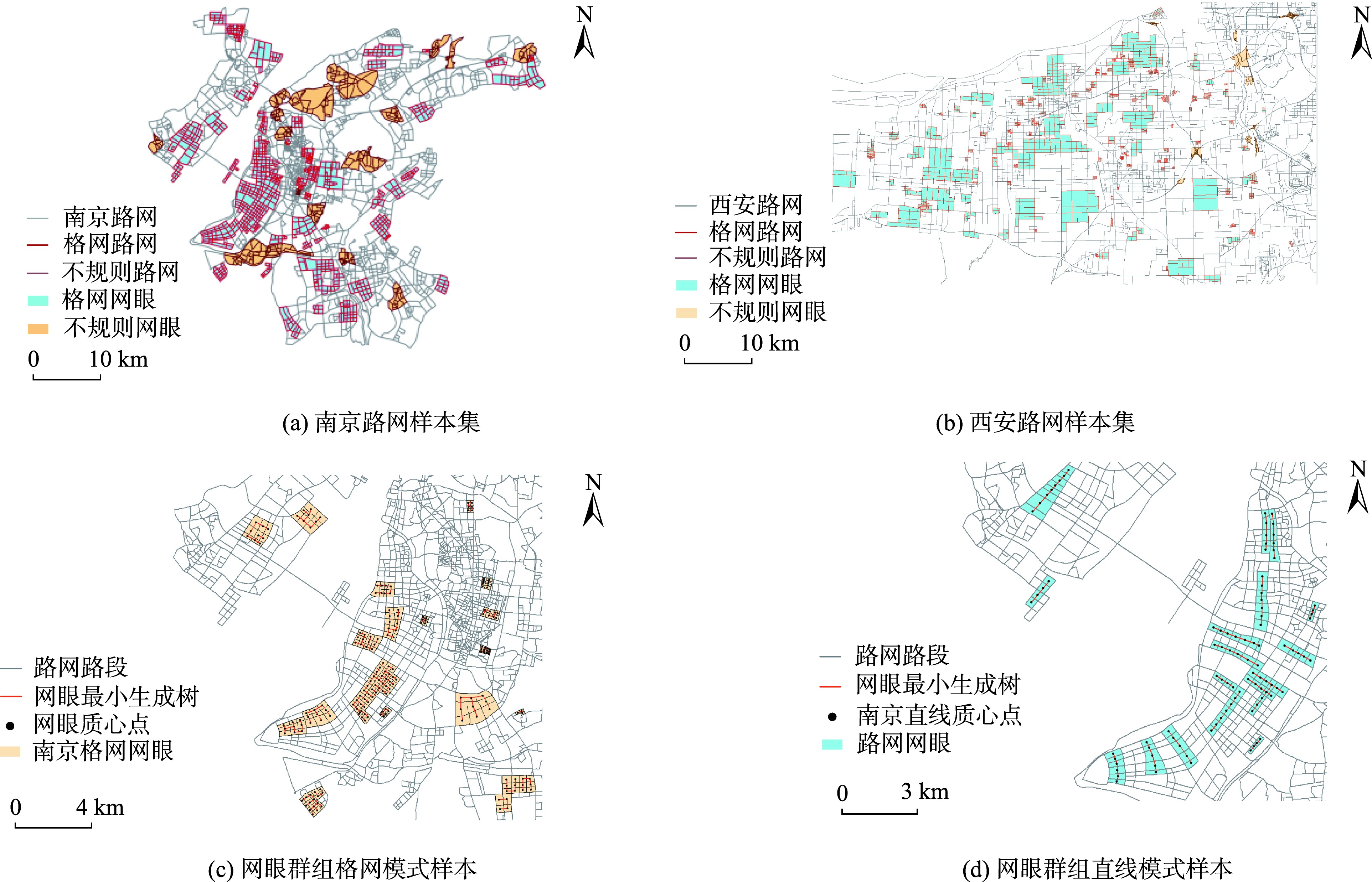
图6 南京市和西安市路网样本
阈值确定结果:
网眼特征参量
矩形度 > 0.75
且凹凸度 > 0.9
路段方向熵
格网路网 < 0.25
不规则路网 > 0.25
网眼最小生成树方向熵
直线型 = 0
格网型 0~2.5
3.2 路网模式识别
为验证所得特征参量的阈值划分是否合理以及算法是否具备可迁移能力,本次实验选用武汉市和上海市道路网进行验证。
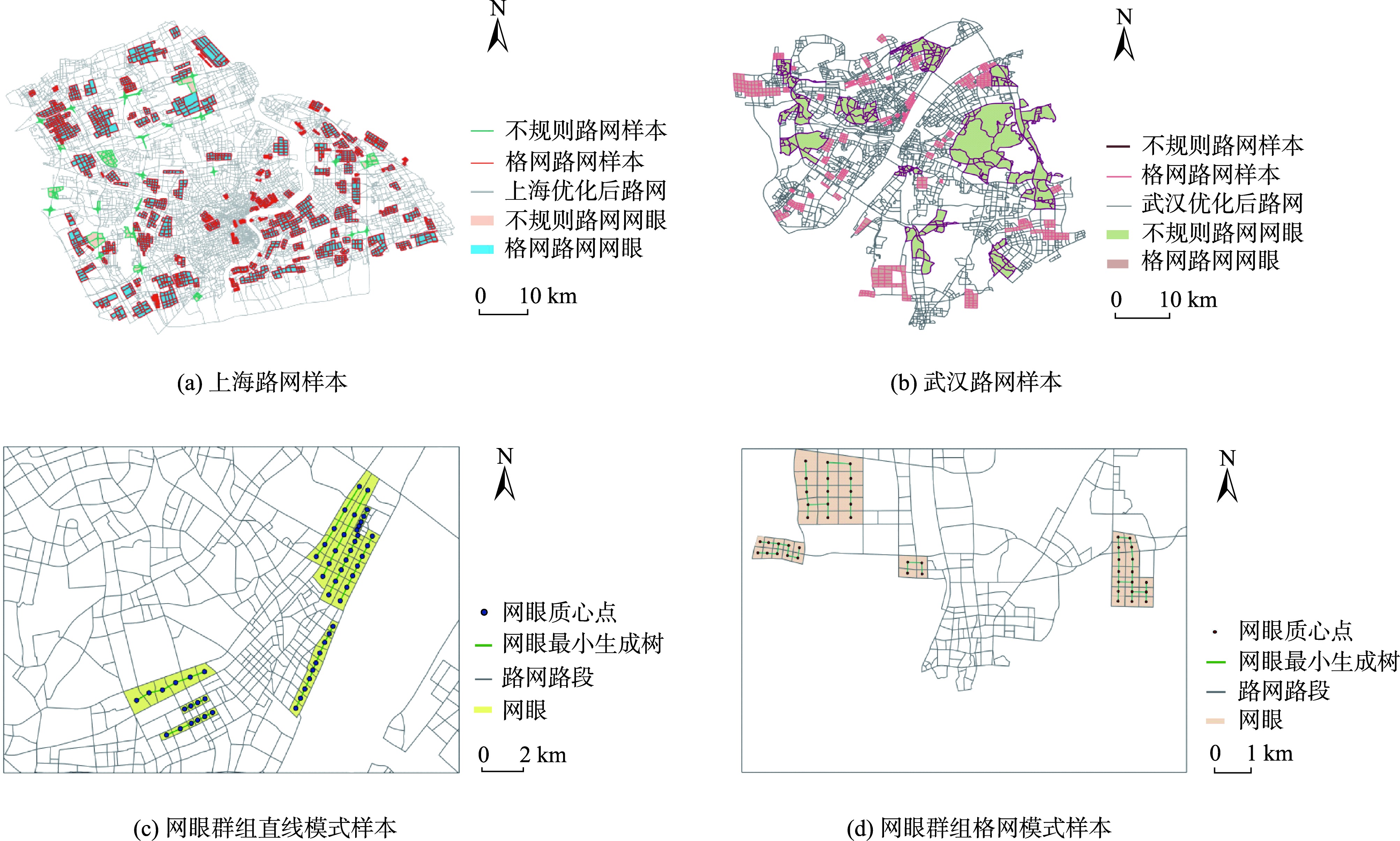
图7 上海市和武汉市路网样本
识别结果统计:
表1 模式分类的准确率、精确度、召回率和F1值
| 类型 | 准确率 | 精确度 | 召回率 | F1值 |
|---|---|---|---|---|
| 格网路网 | 99.33% | 100.00% | 99.25% | 99.62% |
| 不规则路网 | 99.33% | 94.33% | 100.00% | 97.08% |
| 直线型网眼群组 | 98.50% | 100.00% | 97.00% | 98.48% |
| 格网型网眼群组 | 98.50% | 97.08% | 100.00% | 98.52% |
3.3 对比试验
为验证本文方法的有效性,从南京市样本集中选取了80个已标注好的格网路网样本和20个不规则路网样本,分别与Yang等和Tian等提出的基于网眼结构或路段结构的路网格模式识别方法进行对比实验。
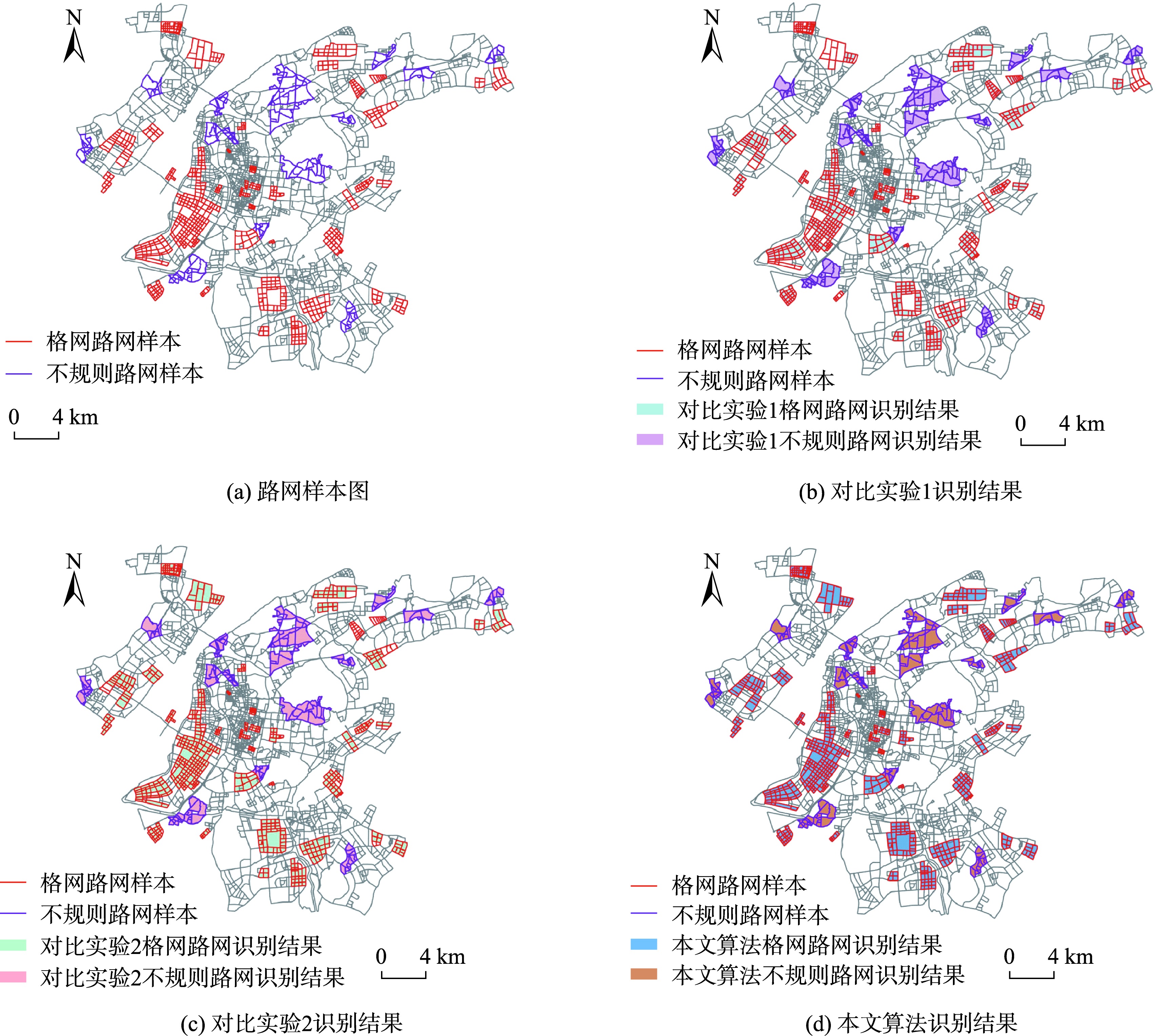
图8 对比实验结果
对比实验结果统计:
表2 对比试验结果
| 实验方法 | 识别出网眼数量 | 未识别出网眼数量 | 样本网眼数量 |
|---|---|---|---|
| 对比实验1 | 992 | 112 | 1,104 |
| 对比实验2 | 1,038 | 66 | 1,104 |
| 本文算法 | 1,104 | 0 | 1,104 |
3.4 问卷分析
为验证以上所得算法是否符合人类视觉认知,从武汉市和南京市道路网样本集中随机选取了10个格网型路网样本和5个不规则型路网样本作为问卷研究对象,选择了80位地图专业相关的老师和学生进行问卷调查。
表3 问卷调查结果
| 标号 | 标注 | 识别结果 | 符合认知程度 | 是否匹配 |
|---|---|---|---|---|
| 1 | 不规则路网 | 不规则路网 | 100% | 是 |
| 2 | 不规则路网 | 不规则路网 | 97.5% | 是 |
| 3 | 不规则路网 | 不规则路网 | 90% | 是 |
结论
路网的模式识别研究在地图制图、地图匹配、城市规划与发展等领域均有诸多应用。为克服已有算法预处理复杂、模式识别单一、网眼群组模式研究较少、算法难度大且迁移能力弱等问题,本文通过结合路网网眼结构和道路路段结构,利用方向熵、矩形度和凹凸度等特征参量,提出了一种简单有效的路网模式识别方法,完成了道路网模式以及路网包含网眼群组模式的识别。
主要研究成果
- 方向熵在描述空间现象方向的分布特征和规律方面具有很大的优势,在路网模式识别中,可定量化描述道路路段和道路网眼群组的排列规整程度
- 提取和构建了路网路段结构、网眼结构以及网眼最小生成树模型,通过计算相应的特征参量阈值完成了格网路网、不规则路网的模式识别
- 根据格网路网所包含网眼排列方式的不同将其划分为直线型网眼群组和格网型网眼群组
- 实验结果表明,本文算法具有较好的可迁移能力且模式识别精度均达到了97%以上
- 通过视觉认知对比和心理问卷调查,发现本文识别的路网模式和网眼群组模式识别结果符合人类认知
不足与展望
本文算法亦存在些许不足,当规整路网中存在近似圆的弧形路段时,将出现错误识别的情况。究其原因,当路网进行线性剖分时,弧形路段会被分割为多条方向不同的直线,导致方向熵计算时,熵值过大,误判为不规则模式路网。该问题有望通过路网预处理的改进或引入新的路网图结构加以解决,这也是我们下一步的研究方向。
* 以上内容由AI自动生成,内容仅供参考。对于因使用本网站以上内容产生的相关后果,本网站不承担任何商业和法律责任。