1 引言

矢量地理数据是国家信息基础设施和地球科学研究的基础性成果，在经济发展和国防建设中发挥着重要作用。作为一种数字产品，极易被传播、篡改和非法复制，为地图盗版、侵权等违法行为提供了极大的便利。因此，研究保障矢量地理数据的安全传播以及追溯非法传播者非常重要。

目前保护矢量地理数据安全的主要手段是数字水印技术，该项技术通过将能够标识数据所有者信息的水印信息嵌入到数据中，达到确认版权归属的作用。但是当多个用户联合起来伪造数据进行共谋攻击时，数字水印无法找出合谋者。

而数字指纹技术凭借特殊构造的指纹编码，通过将唯一标识用户的指纹信息嵌入到数字产品中，能够在多用户合谋攻击下，找出至少一个合谋者且无辜用户不会被诬陷，能够有效的对非法用户进行追踪。因此在盗版数据追踪溯源方面，数字指纹具有数字水印无法比拟的优势。

对称数字指纹

发行商单方面生成指纹信息并嵌入到数字产品中，发行商和用户都拥有含指纹的数字产品。

问题：无法判断非法复制是用户还是发行商所为。

非对称数字指纹

在指纹的生成和嵌入过程有交易双方的参与，交易完成后只有用户拥有含指纹的数字产品。

优势：有效防止合法用户被开发商诬陷。

2 理论基础

2.1 数字指纹编码

数字指纹方案通常需要应对用户的合谋攻击，为此发行商会根据一定规则对用户相关信息进行编码，生成具有抗合谋攻击能力的码字。本文采用的编码方式是利用I码和PD-PBIBD码进行分块编码，以生成抗合谋指纹。

(sp, s2p-2, sp-1, s, 0, 1) GD-PBIBD

其中，s为素数，p为大于2的正整数，通过改变参数s和p构建不同长度的用户码。码字矩阵的总行数表示可以容纳的用户数量，每行均为用户的唯一指纹序列。每个指纹序列中"0"的位置的差异用于唯一标识用户。

2.2 Paillier加密

同态加密算法可以将加密后的指纹信息嵌入到加密后的数字产品中，嵌入完成后使用私钥解密该数字产品即可获得不影响正常使用的含指纹数字产品，因此被广泛应用于非对称指纹协议的构造中。

密钥生成

  1. 随机选取2个不相等的大素数p和q
  2. 计算n = p × q和λ = lcm(p-1, q-1)
  3. 随机选取整数g ∈ ℤ*n²
  4. 计算μ = (L(gλ mod n²))-1 mod n

加密过程

c = gm ∙ rn mod n2

解密过程

m = L(cλ mod n²) ∙ μ mod n

Paillier加密的加法同态性：

D(E(m₁,r₁) ∙ E(m₂,r₂)) = m₁ + m₂

对m₁和m₂的密文进行乘法计算可以得出m₁和m₂的明文相加结果的密文值，本文将使用Paillier加密的该特性进行水印的加密域嵌入。

3 非对称指纹协议

本文协议内容包括指纹生成与嵌入子协议、侵权追踪与仲裁子协议2个部分。协议的核心思想是在数据中嵌入跟踪指纹FT和指控指纹FA两个指纹序列，其中FT由发行商单方面生成和嵌入，FA由用户生成并使用自己的公钥KPU加密后传递给发行商。

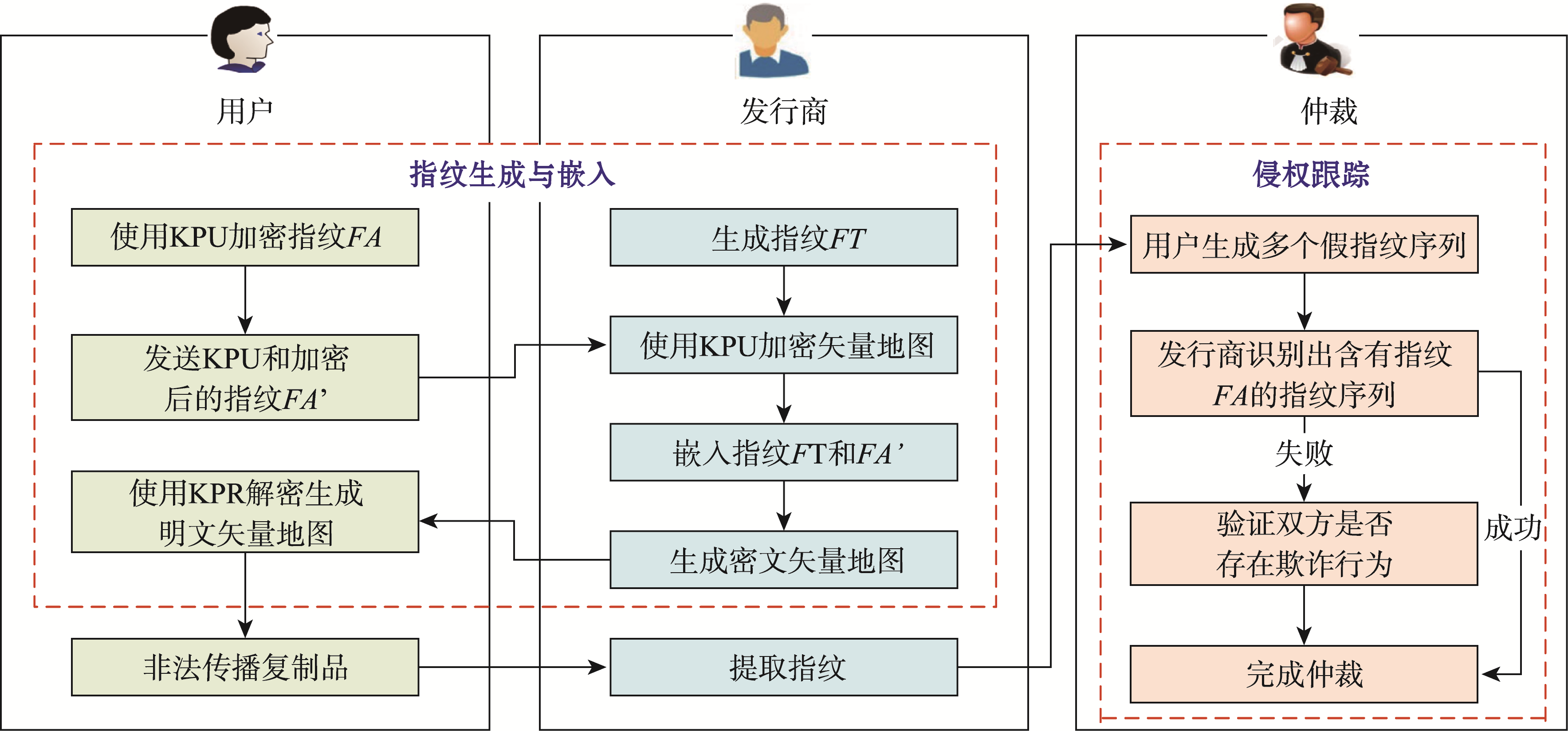
协议整体框架

图1 协议整体框架

3.1 指纹生成与嵌入子协议

指纹生成和嵌入子协议主要负责将交易双方的指纹信息都嵌入到数据中，以便后续发生版权纠纷时使用。设计思路如下：

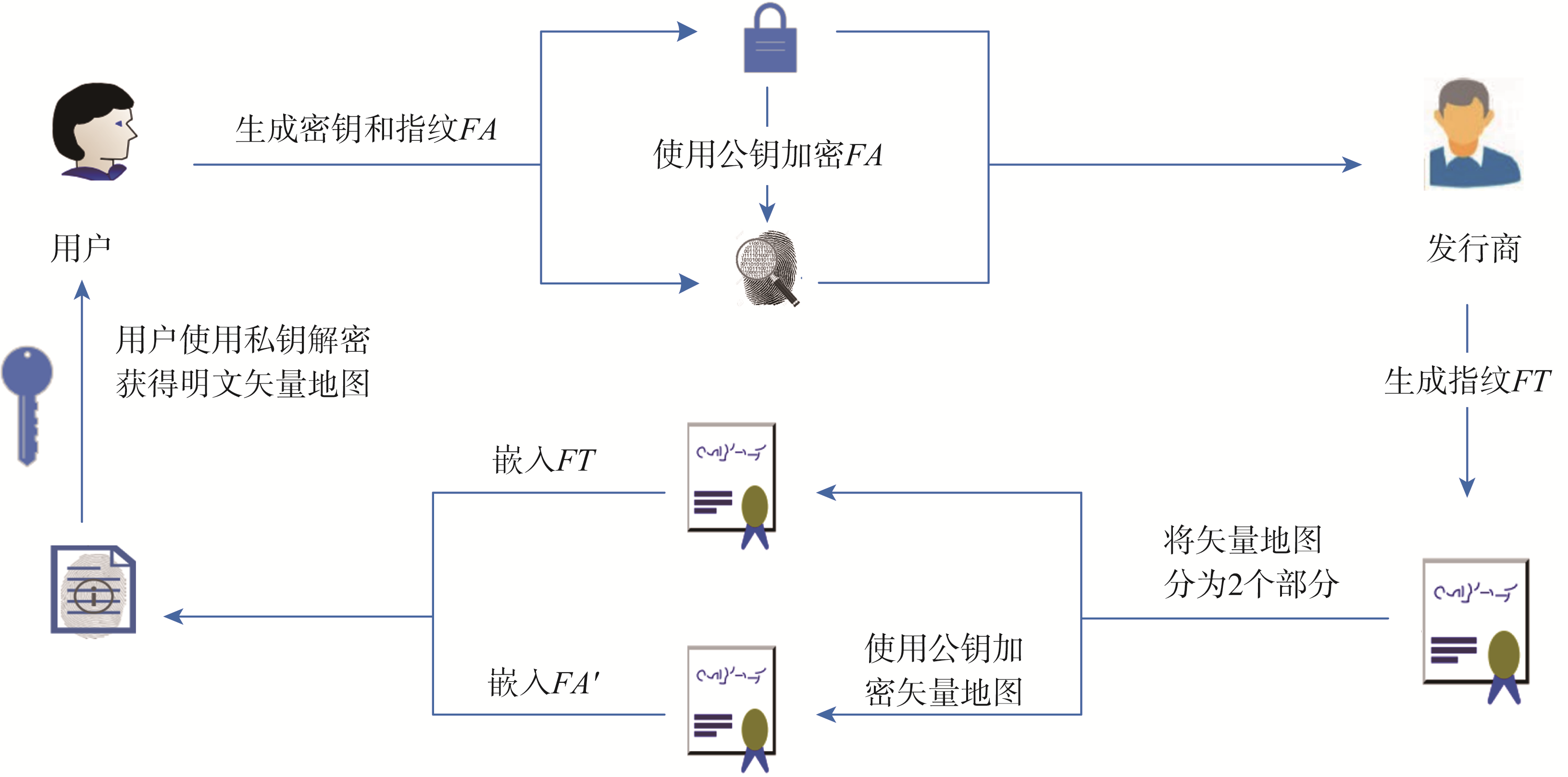
指纹生成与嵌入子协议

图2 指纹生成与嵌入子协议

  1. 用户向发行商发出购买矢量地理数据的请求，发行商将原始矢量地图M分为M₁和M₂
  2. 发行商在自己的指纹库中选取一个指纹序列FT，嵌入到数据M₁中
  3. 用户生成自己的指纹序列FA、公钥Kpublic和私钥Kprivate
  4. 用户使用公钥Kpublic对指纹序列FA加密生成加密指纹FA'
  5. 发行商使用公钥Kpublic对M₂进行加密生成密文数据M₂'
  6. 将指纹序列FA'通过Paillier加密的同态性嵌入到数据M₂'中
  7. 发行商将M₁'和M₂'合并后传给用户，用户解密后获得含指纹的明文数据

3.2 侵权追踪与仲裁子协议

侵权追踪与仲裁子协议主要用于从非法复制品中提取跟踪指纹和指控指纹，使用跟踪指纹追踪非法复制者的身份并在发送侵权纠纷时使用指证指纹协助仲裁。

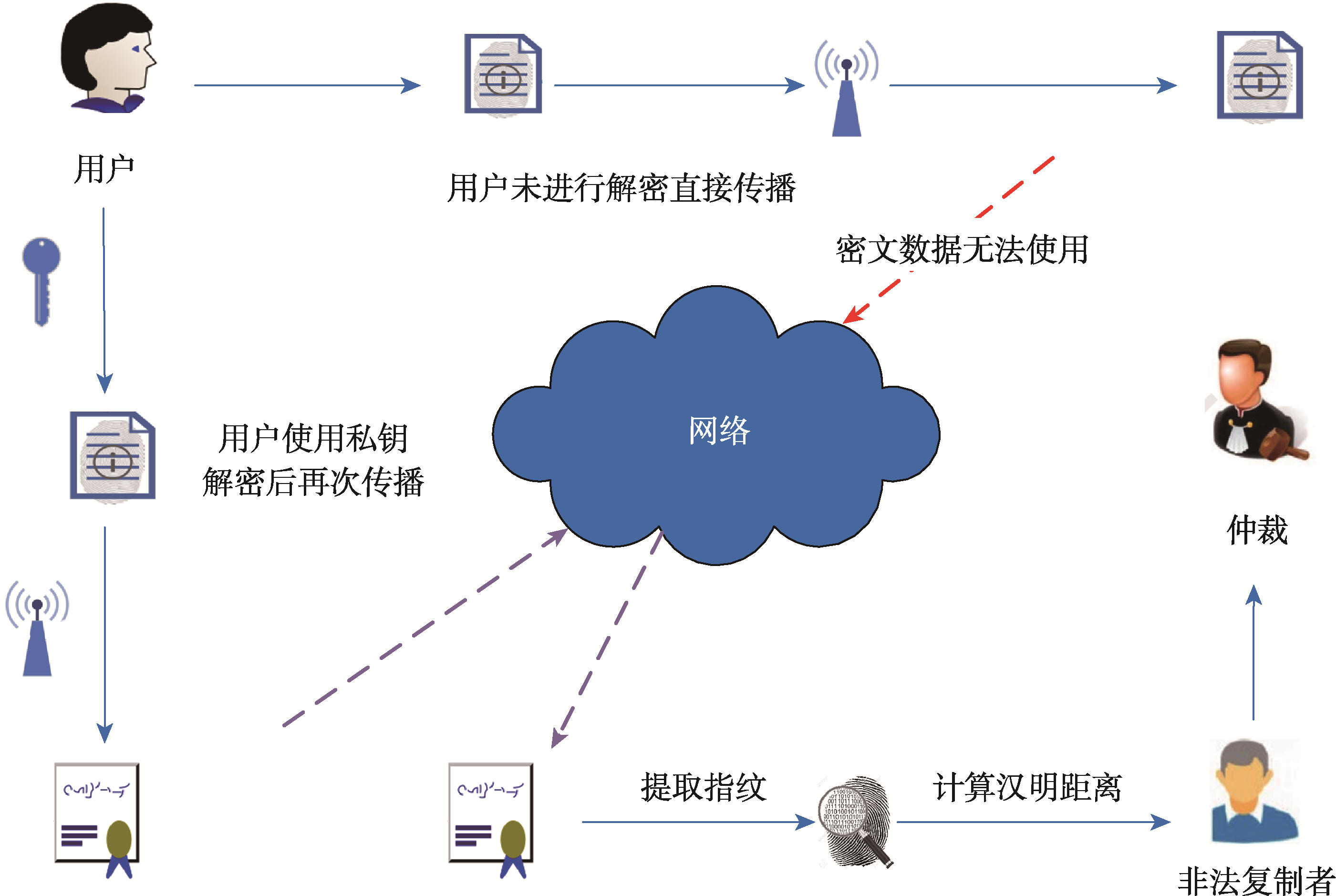
侵权追踪原理

图3 侵权追踪原理

侵权追踪过程

  1. 发行商使用提取算法从复制品中提取指纹信息
  2. 将该指纹序列与发行商指纹库中的指纹序列进行汉明距离计算
  3. 汉明距离最小者即为非法复制者

仲裁验证过程

  1. 用户随机生成2M-1个指纹序列H
  2. 将指纹序列随机分组，2个为一组
  3. 每组中的2个指纹序列相加，组成新的指纹序列NH
  4. 发行商将FA与NH中的指纹序列进行互相关系数计算
  5. 互相关系数最高的序列若与FA相同，则指证成功

4 矢量地理数据的数字指纹算法

本文将2个不同功能的指纹信息同时嵌入到一副矢量地图中，并且为了保证用于仲裁的用户指纹信息不被发行商掌握，需要使用Paillier加密将这个指纹信息加密。

4.1 指纹嵌入

本文中指纹嵌入分为2个部分，分别是跟踪指纹嵌入和指证指纹嵌入。在指纹嵌入前，需要将矢量地理数据M分为2个部分，分别嵌入2个指纹信息。

x' = (x - Valuemin) / (Valuemax - Valuemin) × 10n

跟踪指纹FT嵌入流程

  1. 生成复数序列{ak} = xftk + yftki
  2. 对复数序列进行DFT变换，得到DFT系数{Al}
  3. 在幅度系数中进行指纹嵌入
  4. 进行离散傅里叶逆变换，得到嵌入指纹后的顶点坐标

指证指纹FA嵌入流程

  1. 将Mfa中的坐标值取整到最近的偶数
  2. 使用用户的公钥对坐标和指纹FA进行非对称加密
  3. 利用Paillier加密的同态性将指纹FA嵌入到数据中
  4. 使用嵌入指纹后的坐标值替换原本的坐标值

4.2 指纹提取

当发行商发现了非法复制品时便可以进行指纹提取来确认产品的归属和指证非法复制者。

跟踪指纹FT提取

  1. 读取嵌入跟踪指纹部分的坐标值xFT、yFT
  2. 生成复数序列并进行DFT变换
  3. 根据索引关系进行指纹提取
  4. 使用投票原则获取最终的指纹序列

指证指纹FA提取

  1. 根据x'fa和y'fa的奇偶性进行指纹提取
  2. FA(index) = FA(index)+1, 当x'fa%2=1
  3. FA(index) = FA(index)-1, 当x'fa%2=0
  4. 通过投票原则获取到最终的指证指纹序列

5 实验与分析

5.1 指纹协议的安全性分析

本文的非对称指纹协议是通过将数据先进行加密在嵌入指纹信息，在实现手段与目的上与交换密码水印存在相似性，都存在对数据进行加密和版权信息的嵌入。

安全优势

  • 使用非对称加密，加密密钥和解密密钥不同
  • 传输过程中即使被拦截，也无法解密数据
  • 发行商无法获取含指纹的明文数据
  • 用户解密前无法提取出指证指纹

仲裁安全

  • 用户提供的随机指纹序列越多，发行商指认成功率越低
  • 通过验证条件确保用户无法提供假指纹序列
  • 发行商无法从已知信息推断出用户的明文指纹序列

5.2 算法性能分析

为验证算法的通用性和有效性，对不同类型的3幅矢量地图进行了实验，3幅图的基本信息如下表所示：

表1 实验数据的详细信息
地图 对象类型 大小/KB 坐标数目/个 要素数目/个
A 点 367 13,406 13,406
B 线 15,391 946,115 11,113
C 面 594 36,804 327
加密前后对比图

图4 加密前后对比图

6 结论与讨论

6.1 结论

实验从数据精度、加解密效率、抗几何攻击、抗裁剪攻击以及抗增删点攻击5个方面对算法的效率及鲁棒性进行了分析。在数据精度方面，实验使用了多组不同类型的数据，嵌入指纹的数据与原始数据之间的坐标差值均小于0.001 m，算法对数据的正常使用不会产生较大影响。

算法效率

  • 数据加密效率均值为0.535 MB/s
  • 解密效率均值为0.756 MB/s
  • 仅对部分坐标进行加密，效率优于全数据加密

算法鲁棒性

  • 对平移、缩放攻击具有完全抵抗能力
  • 裁剪50%数据仍能准确提取指纹
  • 增删点40%不影响指纹提取

6.2 讨论

本文利用Paillier加密算法，提出一种适用于矢量地理数据的非对称指纹协议，可以实现对矢量地理数据的盗版追踪和指证。本文协议中，发行商嵌入2个指纹信息到数据中，一个是由发行商生成的用于追踪用户的指纹序列，另一个是由用户生成并加密的指证指纹。

创新点：

  • 利用Paillier加密的同态性进行指纹嵌入
  • 发行商无法获取含指纹的明文数据
  • 无需权威第三方参与仲裁过程
  • 对矢量数据精度影响小
  • 适用于点、线、面三种矢量数据类型

由于非对称加密的特性，相比于对称加密，虽然在安全性上得到了提升，效率却会下降。本算法对矢量地理数据进行加密时，将数据中所有需要加密的点坐标逐个加密，需要加密的点越多，加密需要的时间就越多。因此，在不降低方案的安全性的前提下，如何提高非对称加密的效率是下一步的研究计划。

* 以上内容由AI自动生成，内容仅供参考。对于因使用本网站以上内容产生的相关后果，本网站不承担任何商业和法律责任。