引言

道路作为地理空间数据的基础组成部分，是城市形态的基本骨架，对国家的经济、政治、军事以及人们的日常生活有着重要意义。道路网自动选取一直是制图综合领域的研究热点和难点，对地理空间数据级联更新、多尺度表达具有重要意义。

现有方法

  • 基于stroke的方法
  • 基于语义信息的方法
  • 基于图论的方法
  • 基于道路密度的方法
  • 基于人工智能的方法

研究问题

现有方法主要存在以下问题：

  • 仅考虑单一层次选取单元特征
  • 对语义特征考虑不全面
  • 忽略领域空间特征
  • 过于依赖人工定义规则和设置权重参数

研究方法

本文旨在综合利用路段和stroke的相关特征，基于GraphSAGE图卷积模型对城市中的路网进行自动选取，整体流程如图1所示。

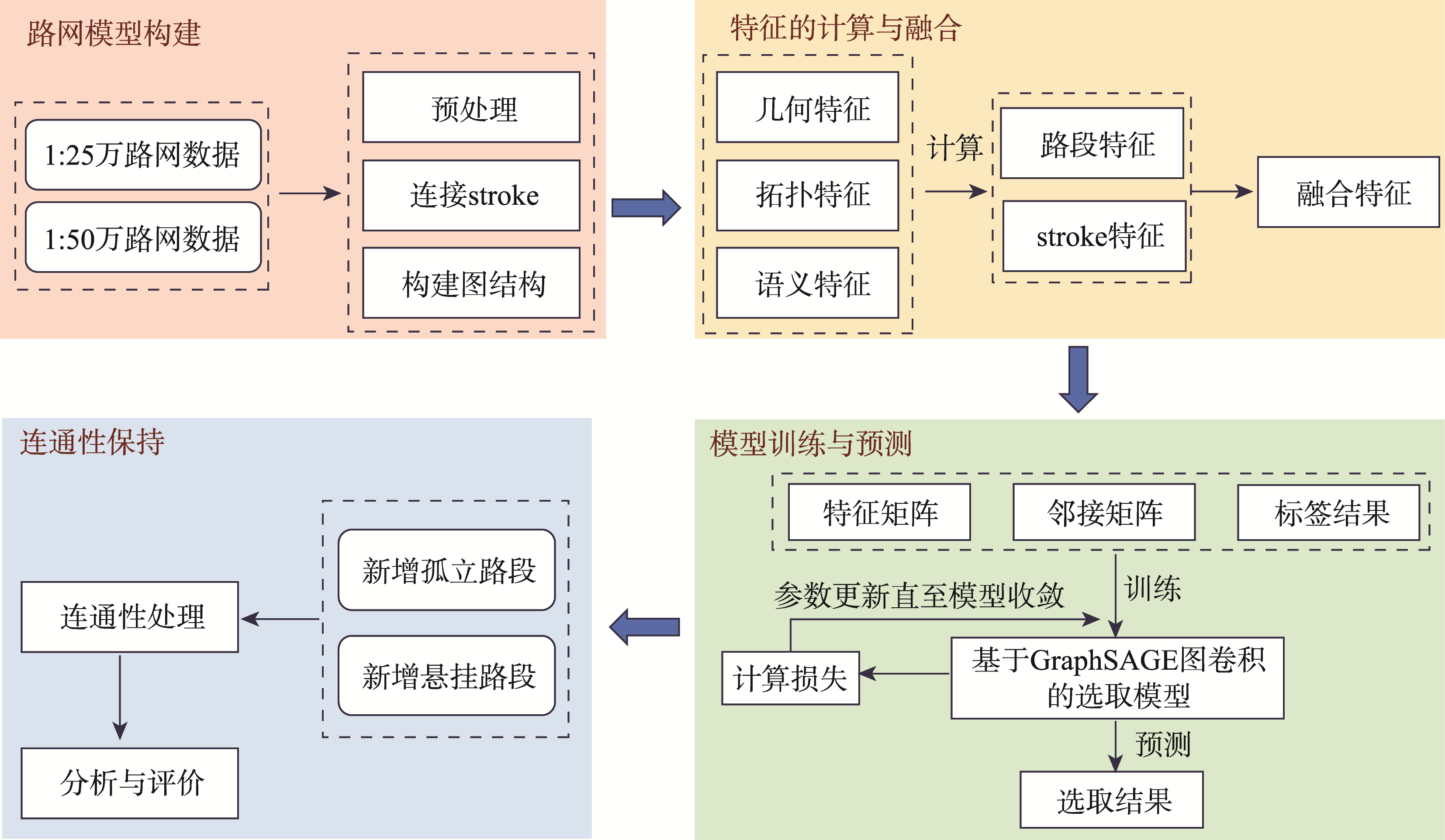
融合路段和stroke特征的道路自动选取方法总体流程

图1 融合路段和stroke特征的道路自动选取方法总体流程

1

路网模型构建

对1:25万和1:50万的路网实验数据进行预处理，并将路段连接成stroke，在此基础上分别构建描述路段和stroke的图结构模型。

2

特征的计算与融合

综合考虑道路的几何、拓扑、属性特征，分别计算路段和stroke的特征，并将stroke的特征融合挂接到相对应的路段上。

3

模型训练与预测

将训练集和验证集的特征矩阵、邻接矩阵以及标签数据输入到图卷积模型中进行训练，并对测试集的选取结果进行预测。

4

路网连通性保持

采用顾及stroke连贯性的连通性保持算法对模型预测后的选取结果进行处理，以便后续分析与评价。

特征指标的计算与融合

路段特征

长度 (Length)

道路选取中最重要、直观的几何特征，可由相邻折点之间的欧式距离累加计算所得。

度 (D)

路网中与某节点相连接的节点数量，表征道路的连通能力。

计算公式：D(vi) = Σδij

中介中心性 (BC)

描述网络中通过某节点的最短路径数量所占比重，体现道路的枢纽特性。

计算公式：BC(vi) = 1/((n-1)(n-2)) * Σ(εjk(vi)/εjk)

接近中心性 (CC)

某节点与其他节点最短路径平均值的倒数，反映道路之间的接近程度。

计算公式：CC(vi) = (n-1)/Σd(vi,vj

类型等级 (GB)

道路选取中重要的语义特征，包括：国道(6)、省道(5)、县道(4)、乡道(3)、城市干道(2)和其他道路(1)。

Stroke特征

长度 (Lenstroke)

同一stroke下所有路段的长度之和，值越大表明对应stroke所占空间范围越广。

计算公式：Lenstroke(vi) = Σlengthj

包含路段数量 (Dstroke)

组成同一stroke的路段个数，值越大表示对应stroke关联的路段越多。

同一stroke下路段的连接数量 (Extension)

描述路段间在stroke上的延续性，取值范围为0、1、2。

特征融合流程

将stroke特征挂接到对应的路段上，具体流程：

  1. 分别构建路段和stroke的对偶图Gv(V,E)、Gs(S,E)
  2. 通过Road_StrokeID字段建立stroke和路段的对应关系
  3. 计算各特征项数值
  4. 将stroke图层中Lenstroke、Dstroke字段值设置到road图层的对应路段上
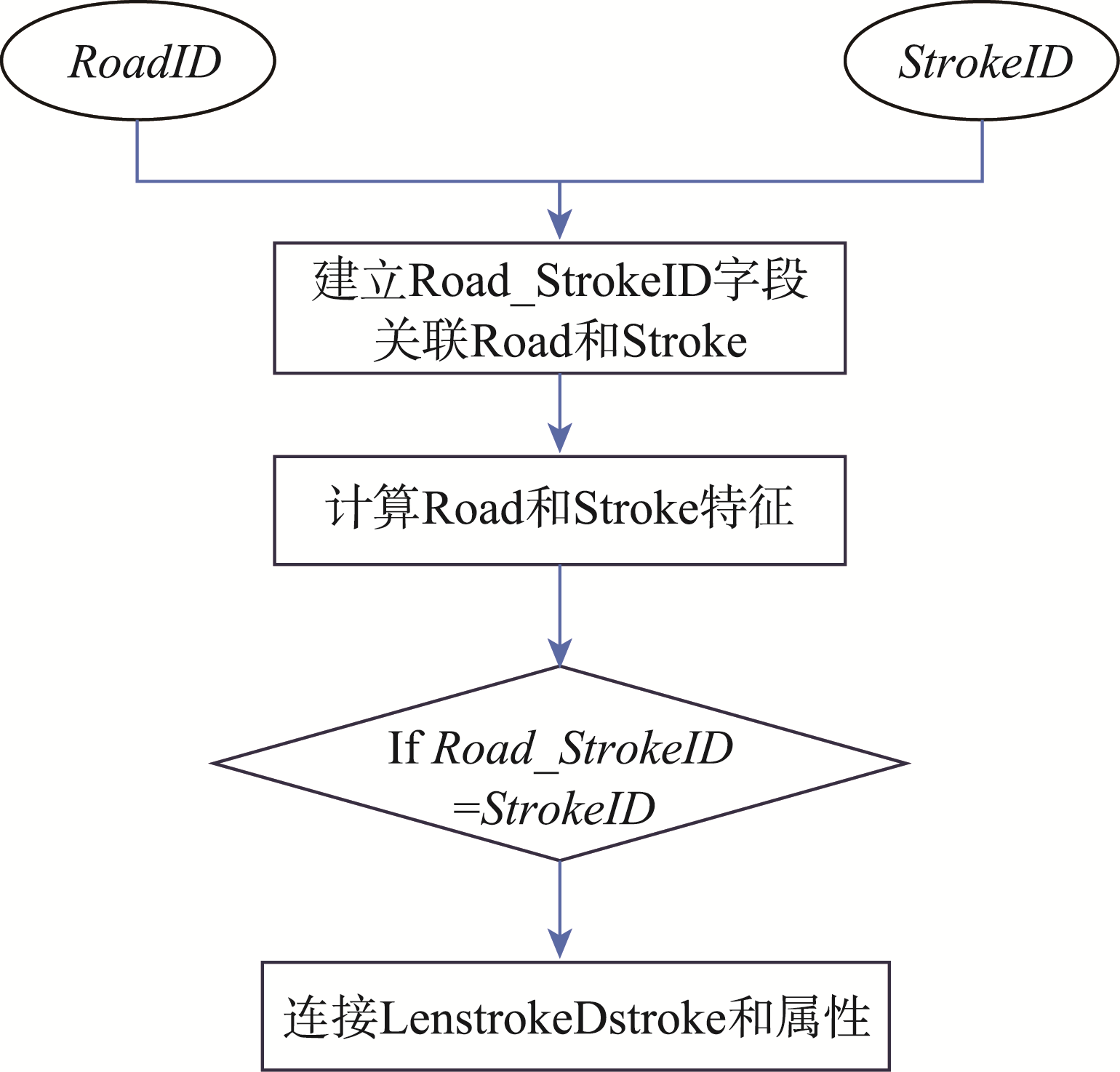
特征融合流程

图2 特征融合流程

GraphSAGE模型构建

核心思想

邻域节点采样

以目标节点为中心，逐层向外随机采样n个邻居节点，共采样K层。

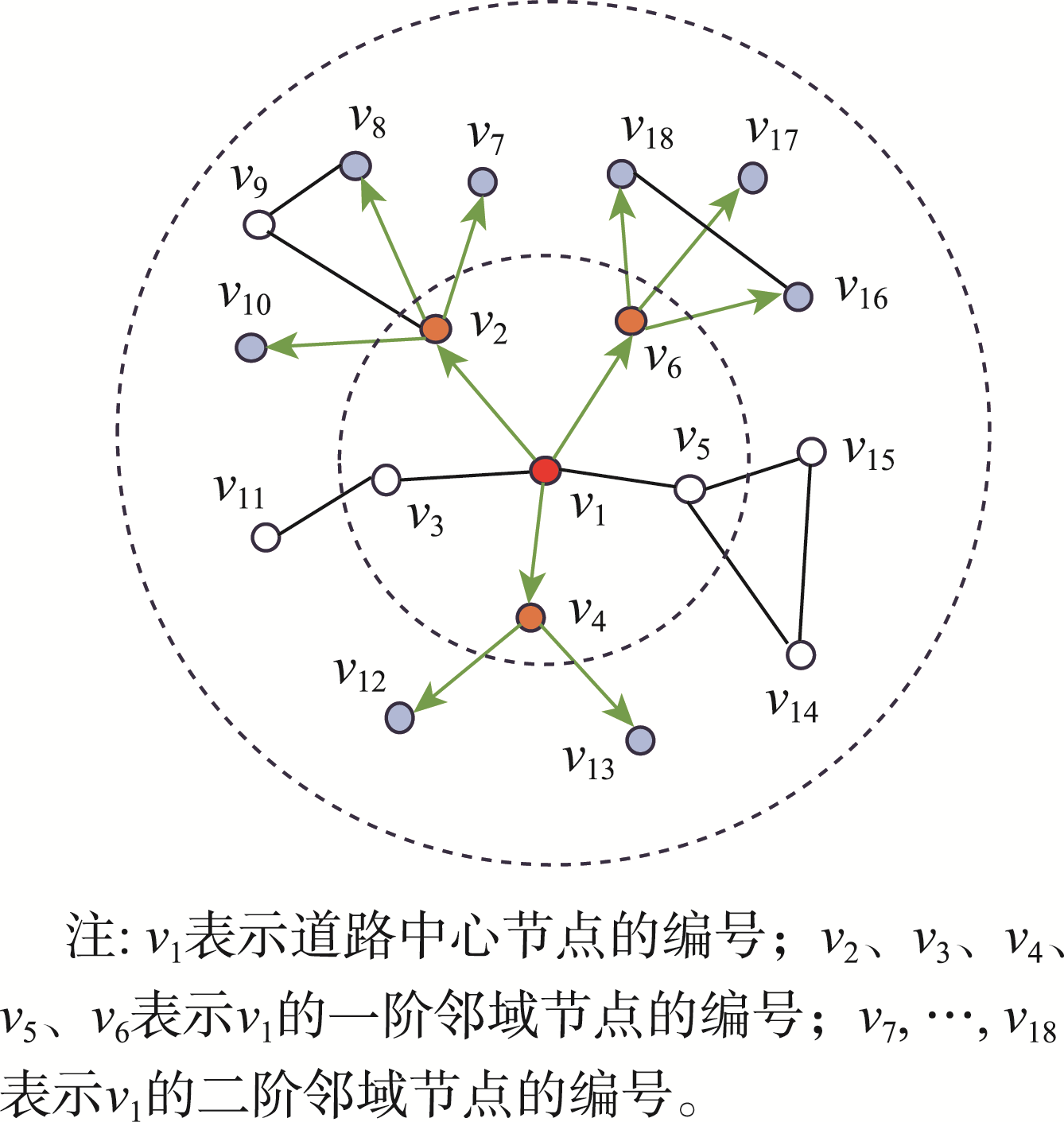
邻域节点采样

图3 邻域节点采样

特征聚合与更新

使用Max聚合方法处理邻域节点特征，并对目标节点特征进行更新。

聚合公式：hkN(v) = max({σ(Wpoolhk-1u + b)}, ∀u∈Nk(v))

更新公式：hkv = σ(Wk·CONCAT(hk-1v, hkN(v)))

模型结构

模型结构

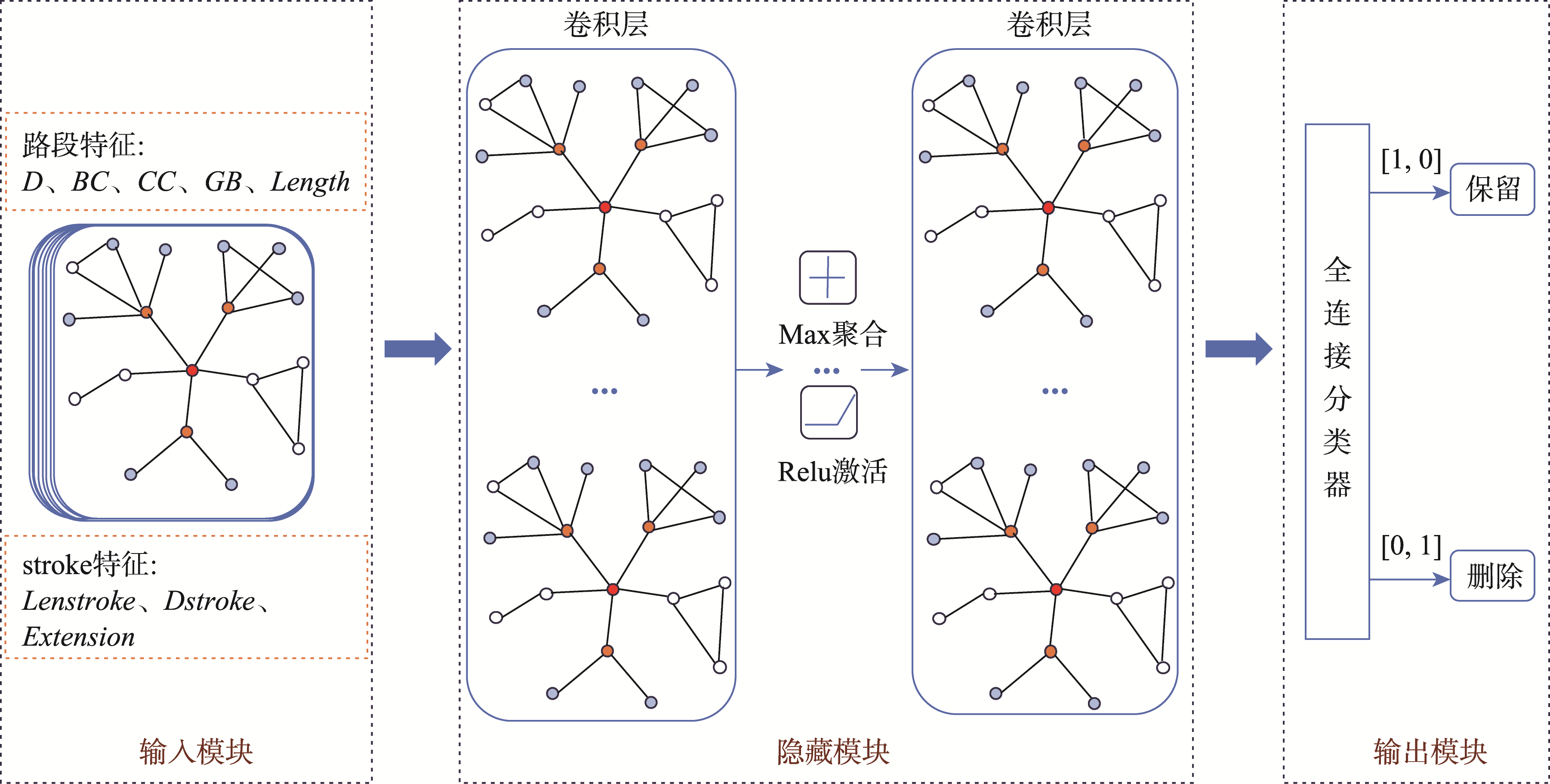
图4 模型结构

输入模块

包括：

  • N×8的特征矩阵X
  • 邻接矩阵A存储路段连接关系
  • 标签Label采用one-hot编码

隐藏模块

包括卷积层和激活函数，GraphSAGE卷积层采用聚合邻居节点特征的方法进行训练。

输出模块

将节点特征输入到分类器中，输出预测概率值判定道路是否选取。

连通性保持算法

道路选取的基本要求是保持路网的拓扑连通性，需要对选取后出现的孤立和悬挂道路进行连通处理。针对选取后的路网，本文提出顾及stroke连贯性的增加最小节点数方法来连通路网。

处理流程

  1. 筛选出选取后出现的孤立和悬挂路段集合L
  2. 针对集合L中的任一路段li，找到对应的stroke弧段Si，若在Si中的部分路段集合Vi能使li连通，将Vi中可使li连通的最小数量的路段组合更新到路网中
  3. 否则利用增加最小节点数的方法，将路段li重新连接
  4. 重复步骤2-3，直至集合L的路段处理完毕

示例

连通性保持示例

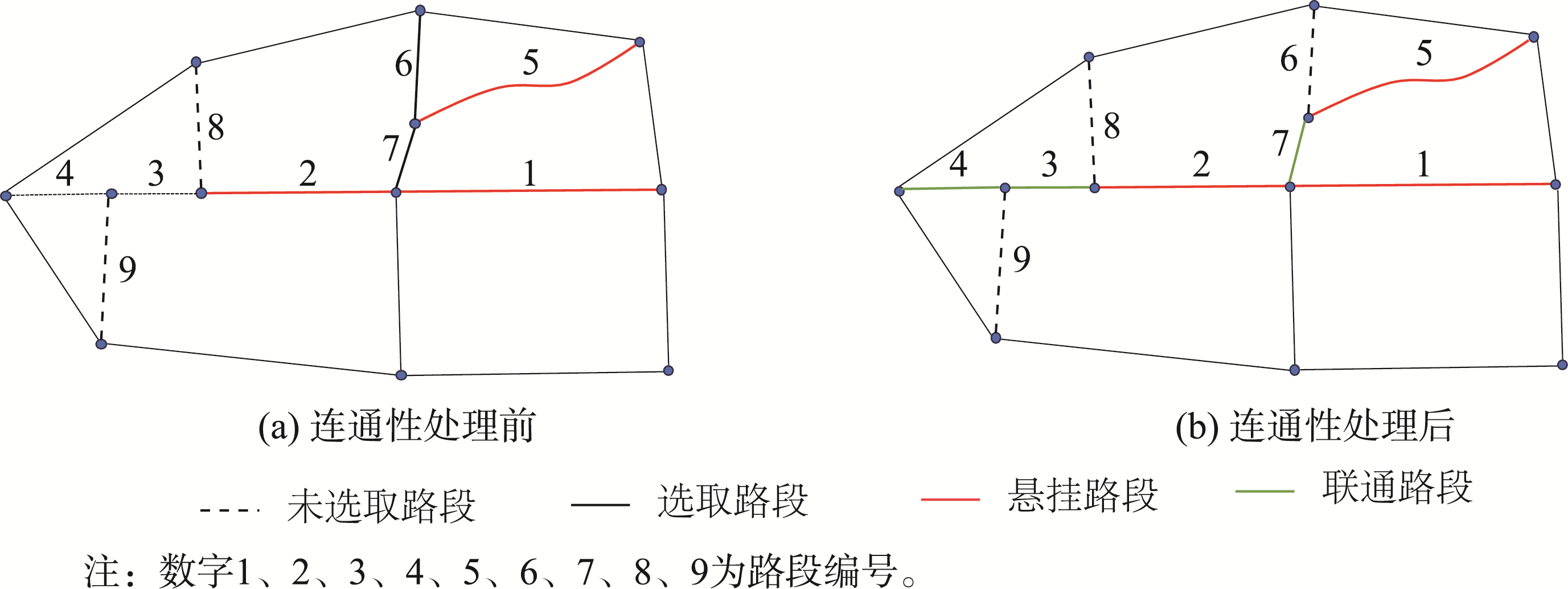
图5 连通性保持示例

图a中路段2和5是选取后需要连通性处理的悬挂路段。对于路段2，和路段1、3、4位于同一stroke下，依据本文方法连接同一stroke下的路段3和4使其连通；对于路段5，由于其单独组成一条stroke，依据增加最小节点数方法连接最短路径下的路段7保持其连通性。

实验与分析

实验数据与处理

选取河南省郑州市1:25万和1:50万比例尺路网数据作为实验和参考数据。

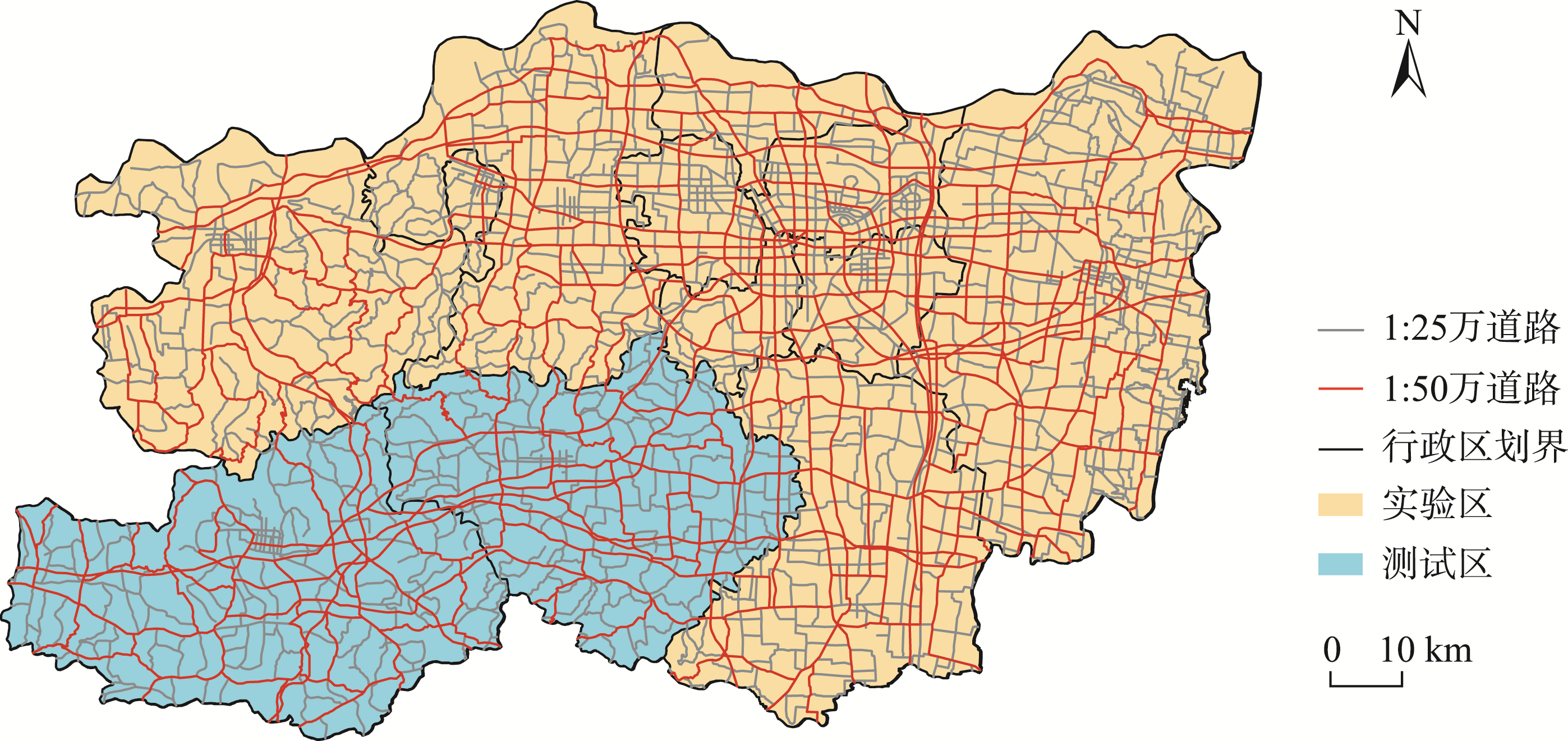
郑州市路网数据

图6 郑州市路网数据

数据规模

  • 1:25万比例尺路网数据包含4,404条路段
  • 构建stroke1,334条
  • 正样本(保留路段):2,064条
  • 负样本(删除路段):2,340条

特征归一化

采用最大最小归一化方法将每个特征计算值映射到0~1之间：

xm = (x - min(x))/(max(x) - min(x))

连通性分析

在未进行连通性保持处理之前：

  • 本文方法新增悬挂或孤立路段为16条
  • 方法1新增了47条
  • 方法2新增了11条

方法1由于未考虑stroke的完整延续性，路网连通性破坏严重。本文方法顾及融合了stroke特征，能很大程度上保持stroke的延续性进而提升路网的连通性。

连通处理后的结果

图7 连通处理后的结果

结论与讨论

主要结论

  1. 特征融合有效性： 综合利用路段和stroke的特征，相较于文献[17]中的方法以及仅考虑单一层次选取单元特征的对比方法，基于GraphSAGE模型的训练和验证结果更优。
  2. 道路延续性保持： 选取过程中充分顾及stroke特征，道路延续性效果明显优于传统以路段为选取单元的对比方法，有效减少后续连通性保持处理的工作量。
  3. 选取效果提升： 连通路网后的最终选取结果在选取密度、一致道路长度和一致道路数量占比3个方面的表现上也均优于2种对比方法，与标准结果最为接近。

存在问题

  • 仅考虑道路本身的特征，未顾及居民地、POI等对道路有明显影响关系的要素
  • 在区域边缘的效果相对不佳，误删和误选比例相较中心区域比重较高
  • 模型训练过程需要大量的人工标注样本，且未考虑模型的泛化性

后续工作

应用范围验证

本文方法适用于中小比例尺城区道路的自动选取，提出的道路特征和模型方法在其他尺度和区域的泛化性需进一步验证与分析。

边缘效应研究

针对本文在区域边缘选取效果略差的问题，深入研究消除"边缘效益"的方法。

特征扩展

结合POI、轨迹、居民地等数据，构建一套更实际、全面的道路重要性参数特征。

样本优化

将基于元学习的小样本学习思想或GraphSAGE模型的无监督学习应用于道路选取中，解决大量人工标注样本的问题。

* 以上内容由AI自动生成，内容仅供参考。对于因使用本网站以上内容产生的相关后果，本网站不承担任何商业和法律责任。