1 引言
地理信息数据资料是地理信息数据生产与应用的基础,随着地理信息数据应用范围不断扩大、应用层次不断深入,用户对全球范围的高质量地理信息数据提出了迫切需求。但是目前境外区域的地理信息数据生产与更新只能依靠从网络上收集到的公开资料进行,收集难度大,收集来的资料凌乱繁杂、现势性差、存在诸多不一致性等问题,严重影响了数据生产的质量和效率。
自发地理信息(Volunteered Geographic Information,VGI)是近年来新兴的开放式地理信息数据,具有高覆盖性、高现势性和易于获取等特点,使其能够成为全球范围内地理信息数据生产与更新的良好数据资料。由于VGI数据的无尺度特性,VGI道路数据细节过于繁杂,远远超出了全球矢量空间数据生产的需要,严重影响了制图人员的处理效率。为此,需要研究VGI中道路的自动选取方法,选择相对重要的、需要保留的道路,删去细小的道路。
目前关于道路网选取方法的研究从传统的基于语义信息的选取,逐渐转向依据道路的几何特征上来。其中,基于图模型的道路网选取方法,凭借其选取后道路连通性优势,近年来得到了广大学者的重视。该方法的主要思路是将道路连接成stroke,并抽象成图模型,并根据图节点的中心性特征构建模型,计算图节点的重要度,进而完成道路选取。这类方法通过对道路的重要度进行量化,进而可以实现道路网的连续尺度变换,但是各个节点中心性之间的权重设置,往往通过人工经验设置,算法的实用程度不高。
此外,还有一些学者引入机器学习的算法,将道路节点的中心性特征作为神经网络的输入,通过监督学习的方法训练神经网络,将道路节点的选取问题作为节点的二类分类问题进行学习。此类方法可以避免不同特征的权重设置问题,但是其将道路网选取作为二类分类问题,只能应用于固定比例尺之间的道路网选取,不能够实现连续的道路网选取。
上述算法,均是直接对待选取道路网建模、计算,从而一次完成道路重要性排序和道路选取。但是在实际进行道路网选取或缩编时,往往是采取逐级选取的策略,如1:5万的道路网要缩编到1:100万,首先要缩编至1:25万,然后再由1:25万缩编至1:50万,最后由1:50万缩编至1:100万。考虑到在逐级缩编的过程中,由于舍去了一些低等级道路,从而会引起道路网结构发生变化,这种结构变化会影响道路的中心性指标,如道路的度、中介中心性等都会发生变化,进而会引起道路重要度排序发生变化。与直接从待选取比例尺计算并完成选取的方式相比,最终的选取结果会产生差异。
为此,本文提出了一种基于道路重要度层次分解的道路网选取方法,借鉴了K-shell算法的逐层分解计算的思想,在进行道路网选取时,通过分批、逐步删除低重要度道路、并重新计算道路网重要度的方式,完成道路网的重要度评价与选取,最后利用实际路网数据对上述算法进行试验验证。
2 研究方法
根据研究目标,本将具体的研究方法分为2个部分:① 道路重要度计算。基于增加加权PageRank算法,在其基础上进行了部分适应性改进和优化,使其能够适用于本文所提出的逐层分解选取的思路。② 道路层次分解选取方法。基于经典的K-shell算法原理,提出了道路重要度K-shell分解方法,使其能够应用到道路网的选取中。
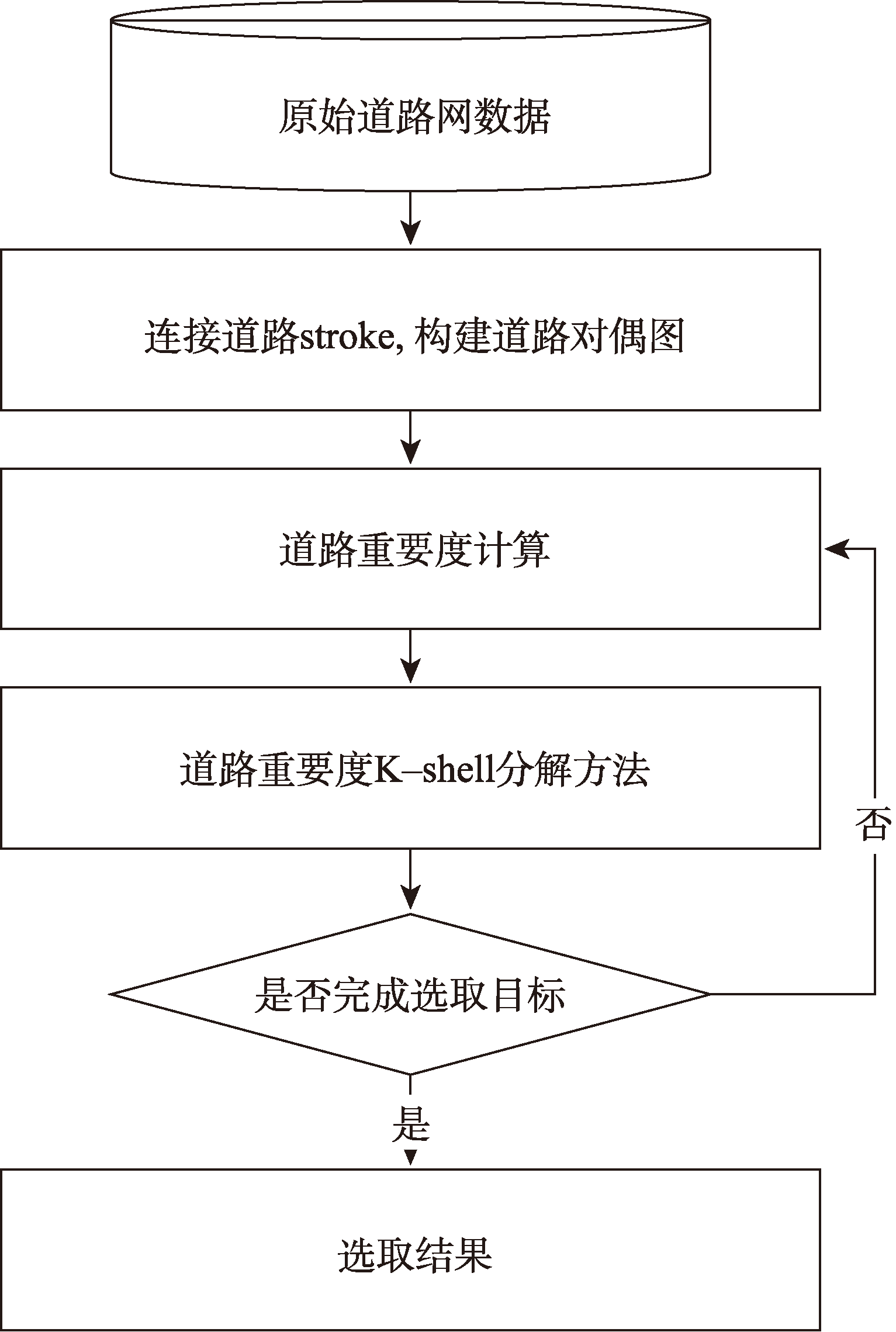
图1 研究技术路线
2.1 道路重要度计算
借鉴PageRank算法计算网页的重要性的思路,本文对加权PageRank的道路重要度算法进行了改进。PageRank算法基本思路为:网页的重要性是由入链的数量和质量决定的,同时每个页面又将自己的重要度通过出链平均分配给其指向的节点。由于PageRank值的排序与初始值无关,因此开始时每个页面设置相同的PageRank值,通过迭代递归计算来更新每个页面的得分,随着每一轮的计算进行,网页当前的PageRank值会不断得到更新。通过若干轮的计算,各个网页的PageRank值会进入一个稳定的状态,得到每个页面最终的PageRank值,该值越大表明该网页越重要。
式中:pi(i=1,2,3,…,N)表示网页节点;InputPi表示节点pi的所有入链集合;|pj Output|表示pi的出链数量;pagerank(pi)表示网页节点pi的PageRank值。为了消除链接陷阱对结果的影响,增加一个阻尼系数d,基本PageRank迭代公式如式(2)所示。
本文在其基础上进行了一定的改进:① 重要度分配权重方法,将道路长度作为道路重要度初始值,将道路当前重要度作为重要度分配权重,这样能够使得重要的道路能够获得更多的权重,并且权重也由静态变为动态,更加能够体现"重要的道路可以获得更多的重要度"这一设计初衷,也可以加快算法的收敛速度;② 去掉了利用SpamRank进行重要度修正的部分,因为本文采用层次分解的选取方法,在逐层分解选取的过程中,逐步去掉了路网密集区域微小道路的影响,可以不用额外考虑。
上述道路重要度计算过程及方法如下:道路网构建道路对偶图,将每个道路节点长度设置为其初始重要度,然后统计各节点的邻居节点情况,并根据当前重要度占比进行邻居节点的重要度分配,通过不断迭代反复,最终达到每条道路重要度不再发生变化,达到稳定状态,此时道路重要度即为所求重要度。
设pi(i=1,2,3,…,N)为道路网中的节点,InputPi表示节点pi的所有邻居节点集合,Outputpj表示节点pj的邻居节点集合,Length(pi)表示节点pi的stroke长度,则节点pi的初始重要度pagerank(pi)0为:
第k次重要度分配时,节点pi获取来自节点pj(pj ∈ Inputpi)重要度时的权重weight(pi,j)k为:
根据上述算法描述,此时节点pi重要度pagerank(pi)k为:
2.2 道路层次分解选取方法
2.2.1 经典K-shell算法
Kitsak等于2010年首次提出了节点重要性依赖于其在整个网络中的位置的思想,并且利用K-shell分解获得了节点重要性排序指标,该指标时间复杂度低,适用于大型网络而且比度、介数更能准确识别在疾病传播中最有影响力的节点。K-shell分解方法通过递归地移去网络中所有度值小于或等于k的节点,是一个层层推进的过程。
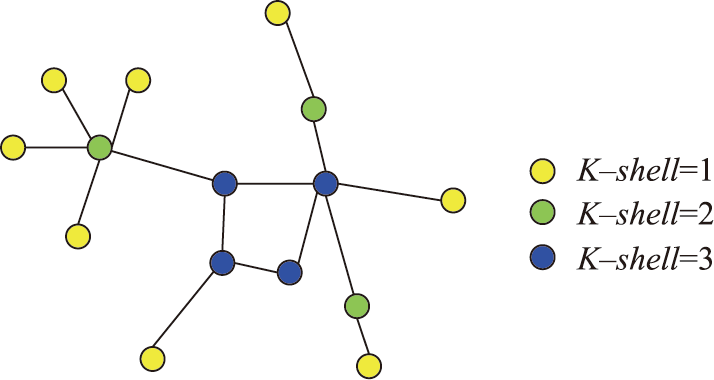
图2 K-shell分解示意图
首先计算图中所有节点的度,然后标记度小于等于1的节点,得到k=1的所有节点,并将其从图中剔除;然后重新计算新图中所有节点的度,继续标记并剔除度小于等于1的节点,得到k=2所有节点;重复上述步骤,直到所有节点分配完毕。这样就获得了一系列不同k核的集合,从而可以将节点进行粗排序。
2.2.2 道路网重要度的K-shell分解
考虑到道路网的逐级缩编过程,即由大比例尺数据首先缩编至较小比例尺,然后再继续缩编,直至到目标比例尺。上述K-shell算法的逐层分解原理,恰好与道路网的逐级缩编相呼应:以大比例尺道路网作为待选取数据,首先根据道路节点重要度评价算法,计算所有节点的重要度,然后舍去一部分重要度最小的道路,得到较小比例尺的道路网,此时的道路网图结构与之前已有所不同,重新计算剩下道路节点的重要度,重复上述选取步骤,直至缩编至目标比例尺停止,即可完成从待选比例尺到目标比例尺的道路网选取。
与现有算法直接根据待选比例尺数据计算道路的重要度并完成最终选取的方法相比,采用逐级选取的方法考虑了逐级选取过程中,道路网结构变化对最终道路重要度的影响,可以更加准确地评价道路的重要度。
本文提出的道路网重要度K-shell分解算法,其具体步骤如下:
输入数据准备
将待选取的道路网数据,构建为道路对偶图G0=(V0, E0),其中V0为道路节点集合,E0为道路连接关系集合。
初始化
设置选取步长step,选取步长表示每次选取时删除的节点数量,step值越小,则选取结果越精细,但计算量也越大;设置选取目标数量target,表示最终需要保留的道路数量;设置当前迭代次数i=0,当前保留的节点集合Vi=V0,当前的道路连接关系集合Ei=E0。
重要度计算
根据2.1节的道路重要度计算方法,计算当前道路网Gi=(Vi, Ei)中所有节点的重要度,得到重要度集合PRi。
节点删除
将PRi按照重要度从小到大排序,取出重要度最小的step个节点,从Vi中删除,得到新的节点集合Vi+1,并更新连接关系集合Ei+1。
终止判断
如果|Vi+1| ≤ target,则算法终止,输出当前保留的节点集合Vi+1作为最终选取结果;否则,令i=i+1,返回步骤3继续迭代。
上述算法的核心思想是通过逐步删除重要度最小的节点,并重新计算剩余节点的重要度,考虑了道路网结构变化对道路重要度的影响,从而能够更加准确地评价道路的重要性。
3 实验与分析
3.1 实验数据
本文选取开放街道地图(OpenStreetMap,OSM)道路网数据作为实验数据,选取区域为某城市中心区域,包含各级道路共计1254条。同时,选取同区域的1:50万基础地理信息数据中的道路网作为参考数据,用于评价算法的选取效果。
3.2 实验设计
为了验证本文提出的基于重要度层次分解的道路网选取方法的有效性,本文设计了以下对比实验:
网络中心性方法
基于网络中心性的道路网选取方法,直接对待选取道路网计算道路重要度,并根据重要度从大到小选取指定数量的道路。该方法是目前常用的道路网选取方法,本文将其作为对比方法。
层次分解方法
本文提出的基于重要度层次分解的道路网选取方法,通过逐步删除重要度最小的节点,并重新计算剩余节点的重要度,考虑了道路网结构变化对道路重要度的影响。
实验中,两种方法均使用2.1节的道路重要度计算方法,以保证重要度计算的一致性。对于层次分解方法,选取步长step设置为10,即每次删除重要度最小的10个节点。选取目标数量target设置为参考数据中道路的数量,以便与参考数据进行比较。
3.3 实验结果与分析
从图4可以看出,两种方法的选取结果都保留了主要道路,但在细节上有所不同。为了定量评价两种方法的选取效果,本文采用以下评价指标:
正确率
选取结果中与参考数据匹配的道路数量占选取总数的比例。正确率越高,表示选取结果与参考数据越接近。
连通性
选取结果中的连通分量数量。连通分量数量越少,表示道路网的连通性越好。
表1 两种方法的选取效果对比
| 方法 | 正确率 | 连通分量数量 |
|---|---|---|
| 网络中心性方法 | 78.3% | 5 |
| 层次分解方法 | 86.5% | 3 |
从表1可以看出,本文提出的层次分解方法在正确率和连通性两个指标上都优于网络中心性方法。这是因为层次分解方法考虑了道路网结构变化对道路重要度的影响,在逐步删除低重要度道路的过程中,重新计算了剩余道路的重要度,使得重要度评价更加准确。
此外,本文还对不同选取步长step对选取结果的影响进行了实验。结果表明,step值越小,选取结果越精细,但计算量也越大;step值越大,计算效率越高,但可能会影响选取精度。在实际应用中,可以根据数据规模和精度要求灵活设置step值。
4 结论
本文针对自发地理信息道路网选取问题,提出了一种基于重要度层次分解的道路网自动选取算法。该算法借鉴了K-shell算法的逐层分解思想,考虑了道路网结构变化对道路重要度的影响,通过逐步删除低重要度道路并重新计算剩余道路的重要度,实现了更加准确的道路网选取。主要研究成果如下:
- 改进了加权PageRank道路重要度计算方法,将道路长度作为初始重要度,将道路当前重要度作为重要度分配权重,使得重要的道路能够获得更多的权重,提高了算法的收敛速度和准确性。
- 提出了基于K-shell分解思想的道路网层次分解选取方法,通过逐步删除低重要度道路并重新计算剩余道路的重要度,考虑了道路网结构变化对道路重要度的影响,提高了选取的准确性。
- 实验结果表明,本文提出的层次分解方法在正确率和连通性两个指标上都优于传统的网络中心性方法,验证了算法的有效性。
本文的研究对于自发地理信息道路网的自动选取具有重要意义,可以有效解决自发地理信息道路数据细节过于繁杂的问题,提高地理信息数据生产的效率和质量。但是,本文算法也存在一些局限性,如需要手动设置选取步长,且步长设置对选取结果有一定影响。在下一步研究中,需要进行更加广泛深入的实验,探索更加合理的步长设置方法,并进一步研究道路选取结果的定量评价机制。
未来的研究方向包括:① 研究更加智能的选取步长自适应调整方法,根据道路网的结构特征和选取目标自动调整选取步长;② 探索将机器学习方法与层次分解方法相结合,进一步提高选取的准确性和效率;③ 扩展算法应用范围,将其应用于其他类型的地理要素选取问题,如水系、居民地等。
引用格式
熊顺,杜清运,马超,等.面向地图综合的VGI道路网重要度层次分解选取方法研究[J].地球信息科学学报,2024,26(1):135-143. [ Xiong S, Du Q Y, MA C, et al. Application of the decomposition importance in the road network auto-selection of volunteered geographic in- formation for map generalization[J]. Journal of Geo-information Science,2024,26(1):135-143. ] DOI:10.12082/dqxxkx.2024.220569
以上内容由AI自动生成,内容仅供参考。对于因使用本网站以上内容产生的相关后果,本网站不承担任何商业和法律责任。