摘要
视觉平衡是影响地图信息传输效果的重要因素之一。由于泛在制图的非专业性,泛在地图图像的视觉平衡效果往往取决于制图者自身美学素养的高低,不具有可控性。因此,迫切需要发展泛在地图图像的视觉平衡度计算方法。现有的地图视觉平衡度计算方法存在因子不全、判别结果主观依赖性强等问题。
针对这些问题,本文提出了一种结合地图图像计算特征与专家评价知识的泛在地图图像视觉平衡度计算框架。通过丰富地图视觉密度影响因子,并引入概率模型学习专家对泛在地图图像的评价知识,实现对泛在地图图像视觉平衡度复杂分布的有效判别。
本文以专家问卷的方式搜集了30名地图制图专家对1 730幅泛在地图图像的视觉平衡评价数据,构建了一个泛在地图图像视觉平衡度评价数据集。将计算得到的地图视觉平衡指标作为贝叶斯决策器的地图特征属性输入,将地图视觉平衡的专家评价数据作为贝叶斯决策器的分类结果,利用最小错误率贝叶斯决策方法对泛在地图图像的视觉平衡度进行判别,有效解决了人为主观判别地图视觉平衡度存在的不确定性问题。经实验验证,该框架在本文构建的泛在地图图像视觉平衡度评价数据集上能取得82.85%的评价准确率。
关键词:
1 引言
视觉平衡是心理学、心理物理学以及艺术领域的重要研究内容。对地图这一融科学与艺术为一体的产物而言,视觉平衡是影响其科学性和艺术性的重要因素,是地图设计的重要关注点之一。在地图学中,视觉平衡是指地图布局中不同地图组成部分排列的视觉稳定性及其视觉冲击力,需要按照一定原则根据观察的客观对象的视觉变量给予其应有的地位,从而达到各要素的关系合理、协调,具有平衡感的视觉效果。
具备视觉平衡特点的地图:
- 版面合理、层次分明且内容准确
- 各图面要素的配置既满足摆放灵活、多样统一、对称均衡的特点,使图面有"精神",又不干扰地图主体
- 相对重要的要素应出现在更加突出的位置,占据更大的"纸张"面积,这样能使地图读者更易于专注地图的内容
而不具备视觉平衡的地图,会使地图读者感到困惑或反感,只能获取到部分地图信息。
传统上地图均由经过培训的专业人员制作,遵循地图设计的一般规律。但随着泛在制图技术的发展,专业和非专业制图者均可借助网络平台和开源制图工具设计、制作、发布地图,且出于网络发布与传播便捷性考虑,多以图像形式在互联网上传输应用,本文将这类地图图像统称为泛在地图图像。
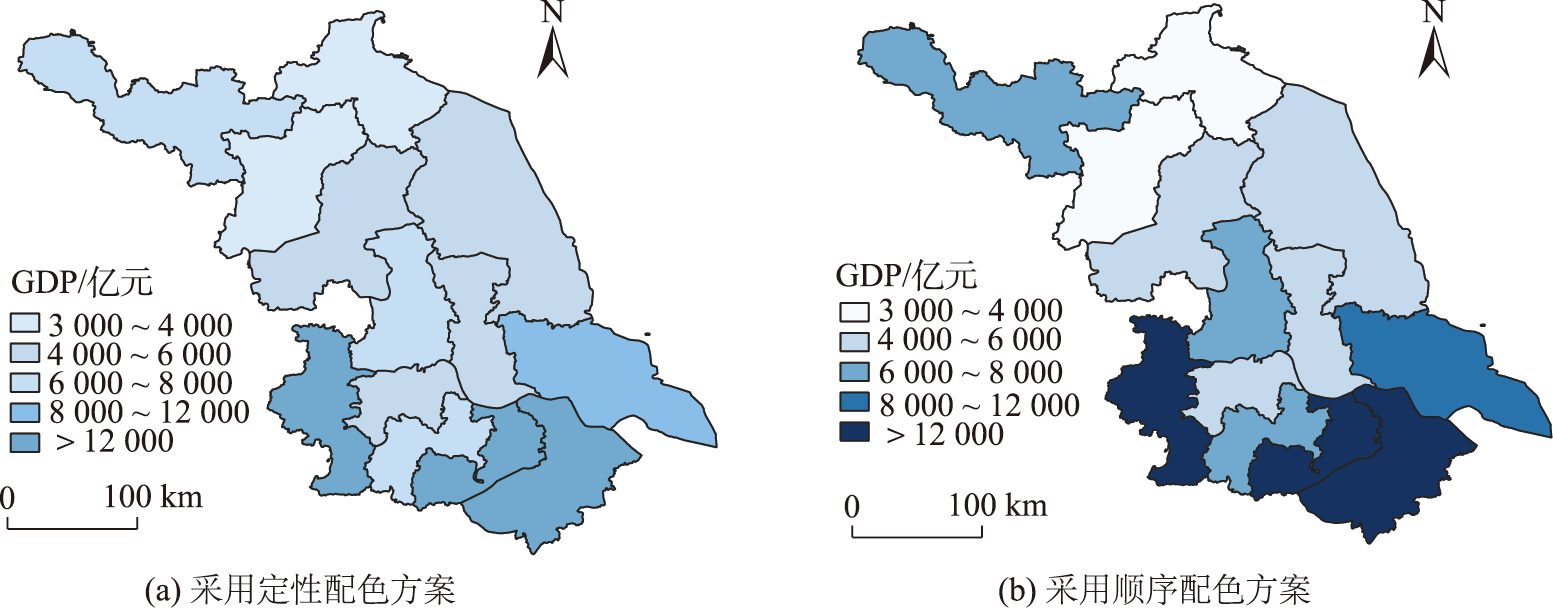
图1 采用不同色彩设计的地图对比(2020年江苏省各市GDP为例)
从物理存储方式上来讲,泛在地图图像属于栅格电子地图的一种,但其呈现出来源广泛、表达多样、主题丰富的特点。同时,其存在的问题也非常突出,即并非所有都遵循制图规范,在符号、色彩、图面配置等设计方面水平参差不齐,使其作为一类地理信息资源的价值降低。特别是对于泛在地图图像的视觉平衡,往往取决于制图者自身美学素养的高低,成为影响信息传输效果的重要因素之一。
因此,迫切需要发展能够定量计算泛在地图图像视觉平衡度的模型,对泛在地图图像进行视觉平衡评价,一方面可以过滤部分视觉平衡度较低的地图图像,把控检索质量;另一方面为评价泛在地图图像作为地理信息资源的美学价值提供参考。当前,地图学界对于地图的视觉平衡度计算模型已有一些研究成果,但总体还存在考虑因子简单、判别结果主观依赖性强等问题。本文瞄准上述问题,基于力矩平衡原理,构建一种基于多因子贝叶斯决策的泛在地图图像视觉平衡度定量计算框架。通过该框架对泛在地图图像的视觉平衡进行评价,有利于指导泛在制图过程中对于视觉平衡的把握,从而提高泛在地图图像的资源利用价值,促使泛在制图更符合地图设计规律。
2 视觉平衡评价研究现状
视觉平衡的概念,发端于艺术领域。格式塔心理学家Rudolf Arnheim奠定了视觉平衡的理论基础,他认为视觉平衡是空间构图的组织原则之一,构图通过视觉元素的排列创造出一个独立的、平衡的整体。每个视觉元素都具有感知重量(感知力)。具有感知重量的视觉元素包括位置、空间深度、尺寸、形状、颜色以及读者固有的兴趣等。视觉平衡则是"构成视觉结构的感知力在二维空间中相互补偿的动力状态"。视觉元素在作品中的排列决定了一幅画的平衡程度。这些基本理论成为视觉平衡度计算方法的基础。
鉴于视觉平衡对地图信息传输效果具有重要影响,在地图设计领域,一些学者围绕地图视觉平衡的影响因素、影响模型及其度量计算开展了诸多有益探索。马俊等总结了影响地图视觉平衡的因素,提出视觉平衡是由各个图形单元的视觉重量和视觉方向决定的,并提出了一种基于力矩平衡原理的视觉平衡度计算模型,实现了视觉平衡从定性评估到定量计算的转化。但是该方法选取的计算因子相对简单,如颜色并未将色彩对比因素考虑在内等。
图1是采用不同的配色方案对同一份地图数据进行绘制的地图图像,可以清楚地看到其产生的视觉平衡感是不同的。右图相较于左图而言,由于其主图图面右下方区域的颜色与背景产生了强烈对比,导致整幅地图的视觉中心偏向于右下方。
魏智威等通过计算地图图面的视觉中心与理论视觉中心的距离,来判断地图视觉平衡的好坏,但是该方法只适用于计算地图主图的视觉平衡。徐建新等针对地图图像,基于力矩平衡原理,采用图像处理领域的灰度分布均衡方法,提出了一种定量测度地图图像视觉平衡质量的新模型,但该方法忽略了形状因子的计算,并且对于颜色因子的量化采用图像的灰度值来进行代替,存在计算不够准确的问题。可见,目前虽有针对地图视觉平衡度计算模型的研究,但总体上较为零散,考虑的因子相对简单;对于定量计算结果如何转化为视觉平衡的结论,还存在主观性强的问题。
视觉设计领域关于自动布局、用户界面评价的研究成果也对地图视觉平衡计算具有重要的参考价值。Yang首次探索了机器理解视觉平衡的新方法,并提出视觉平衡是一种状态,在这种状态下,视觉权重被平均分布在页面上,视觉对象的各个视觉变量都会影响视觉权重的大小。Lok等研究了自动布局的视觉平衡评价问题,定义了重量映射图(WeightMap)的概念和方法,提出视觉平衡可分为对称平衡、不对称平衡、径向平衡和晶体平衡四种类型,并针对晶体平衡构建了重量映射金字塔模型。
Obrador针对文档布局提出了一种兼顾色彩协调、视觉平衡以及图像质量的计算方法。Zhou等基于力矩平衡原理,提出了一种针对机架面板界面设计的视觉平衡度量方法,并建立了一个设计优化的评价模型。另外,随着人工智能技术的快速发展,智能算法也被应用于解决这个问题,Jahanian等利用深度学习技术从大规模的图像数据集中学习视觉平衡,但是由于地图图像中的符号、文字等内容的颜色、纹理、尺度差别较大、质量各异,甚至存在相互重叠的情况,这可能导致依赖于地图图像数据的质量和数量的深度学习模型出现噪声较多的问题。以上方法针对图文布局领域的视觉平衡度进行量化计算,也为研究地图的视觉平衡扩展了思路。
3 泛在地图图像视觉平衡度计算框架
3.1 框架概述
Rudolf Arnheim借用物理学中力的概念来描述艺术作品中不同视觉元素给人的主观感受,并指出平衡即为作品"势能"最小。因此,在构建地图的视觉平衡度计算模型时,多数借鉴了这一思想。地图通过图面主区和一组图面辅助元素来共同反映客观事物的位置、属性及事物间的关系。图面主区和各个图面辅助元素通过视觉变量及其组合产生视觉平衡的主观感受。对遵循设计规范的地图而言,其视觉平衡感受往往较为稳定,采用多因子定量描述的加权求和方法和地图样本视觉平衡度指标的算术平均的阈值设置方法能有效地计算和判别其视觉平衡度。
但是,泛在地图图像获取来源广泛、制图用途多样,既包括专业地图制图人员的成果,也包括大量由非专业制图人员设计的作品,其视觉平衡感受往往存在较大差异,采用上述方法无法有效处理不同视觉平衡度间存在重叠的复杂分布情况。针对这类问题,本文提出了一种结合地图图像计算特征与专家评价知识的泛在地图图像视觉平衡度计算框架(图2),通过丰富地图视觉密度影响因子,并引入概率模型学习专家对泛在地图图像的评价知识,实现对泛在地图图像视觉平衡度复杂分布的有效判别。
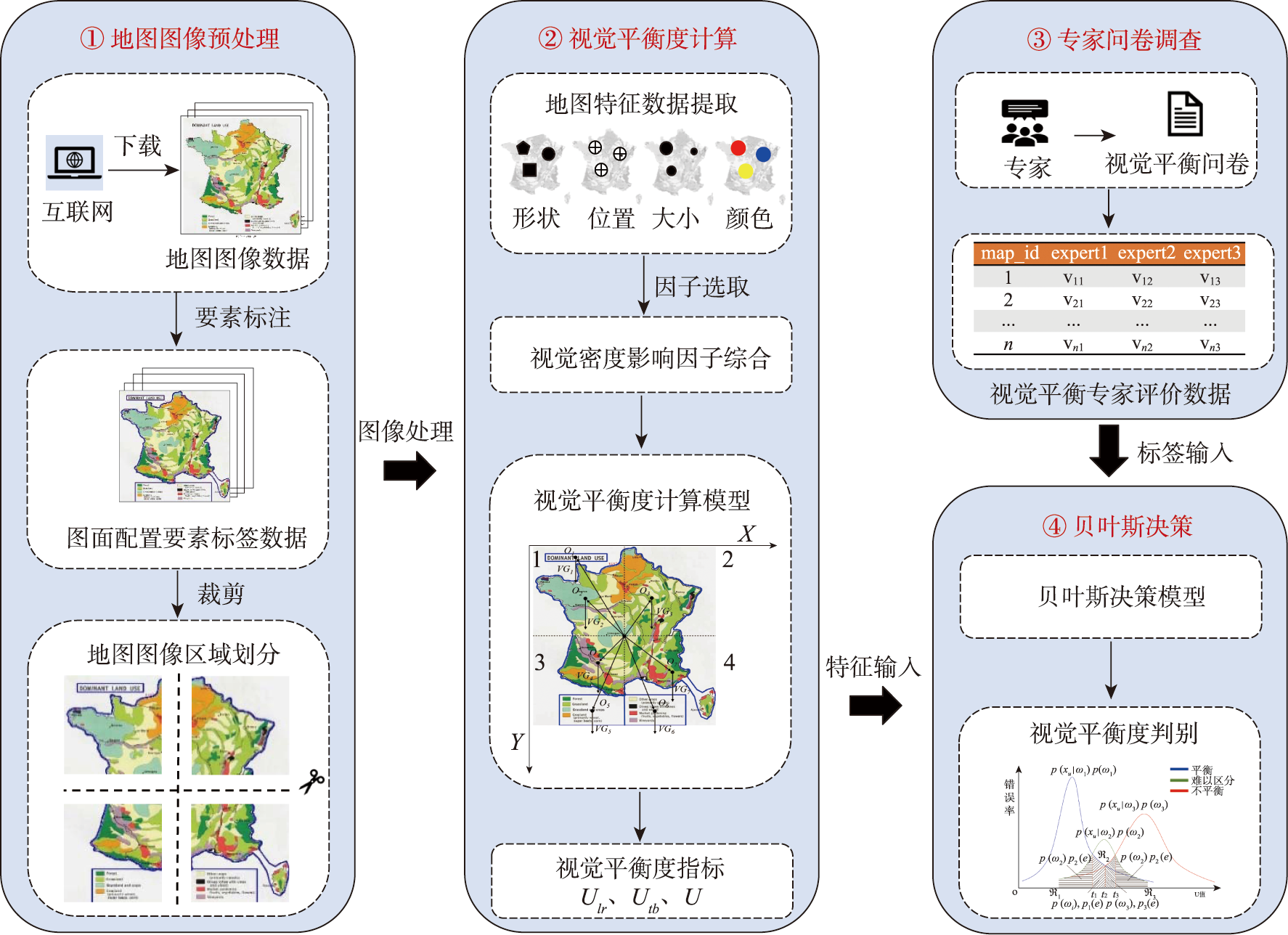
图2 泛在地图图像视觉平衡度计算框架
该计算框架主要由地图图像预处理、视觉平衡度计算、专家问卷调查、贝叶斯决策4部分构成。
- 地图图像预处理:首先使用互联网搜索引擎搜集地图图像,其次采用人工标注或特征自动提取的方式,从地图图像中提取主图和图面辅助要素(即以多边形框选的形式,确定这些要素在图像上的位置范围及要素类别)获得主图和图面辅助要素的标签数据,最后对这些标签数据进行区域划分,便于下一步图像处理与指标计算。
- 视觉平衡度计算:首先,基于地图图像预处理得到的结构化标签数据,采用图像处理技术提取其特征数据 X =[x1,x2,…,xn]T,其中包括形状、位置、大小、颜色等特征。其次,确定地图图像视觉密度的影响因子及其定量描述方法,本文选取了颜色、形状、位置这3个因子,并对其进行多因子综合,得到地图图面配置的视觉密度值。最后,将上述特征数据和视觉密度值代入到设计好的地图图像视觉平衡度计算模型 U = f(ρi,Si,Li)中进行计算。得到每幅地图图像的视觉平衡度指标Ulr、Utb和U。
- 专家问卷调查:为获得泛在地图图像的视觉平衡度指标对应的平衡度分布,以问卷调查的方式获得的专家对每幅地图的视觉平衡性评价数据,作为指导泛在地图图像视觉平衡度判别的统计先验。本文构建了泛在地图图像样本数据集,设计了视觉平衡度调查问卷,将泛在地图图像视觉平衡度分为平衡、难以区分、不平衡3类判别结果,依托互联网平台问卷工具开展相应的问卷调查,获取地图制图专家对泛在地图图像的视觉平衡度评价数据。
- 贝叶斯决策:基于地图图像平衡度指标数据和相应的专家评价数据,通过参数估计构建一个反映泛在地图图像视觉平衡度真实分布的概率模型 yi = f(xU,ωi),并应用该模型基于泛在地图视觉平衡度指标进行视觉平衡度判别。本文采用左右平衡指标Ulr、上下平衡指标Utb和总体平衡指标U作为视觉平衡度描述特征,专家评价数据作为判别真值,构建了最小错误率贝叶斯决策模型进行视觉平衡度的判别。
需要指出的是,上述计算框架虽基于泛在地图图像采用地图特征计算与专家评价知识结合的方式进行实现,但框架中的部分内容,如视觉平衡度指标的计算和基于贝叶斯决策的视觉平衡度判别可面向一般地图图像,并且可以根据地图数据特点和评价需求进行相应的改进与扩展。针对不同类型的地图数据资源可通过专家问卷的样本数据进行选择,从而应用于不同类型地图的视觉平衡度判别。本文后续三节将对该计算框架的基本设计与实现进行介绍。
3.2 地图图像视觉平衡度计算模型
地图图像的视觉平衡度评价本质上是评判地图主图和图面辅助要素的空间布局是否平衡,可通过设计一个视觉平衡度计算模型定量地反映地图图像的视觉平衡程度。Zhou提出了一个针对界面组合设计的视觉平衡优化模型,通过将一个界面分成4个区域,并分别计算其各自的视觉重量,然后计算出整个界面视觉平衡值,最后根据该值的大小对其界面进行优化,方法简单高效。本文针对地图图像的特点,在该模型的基础上,提出了一个基于力矩平衡的地图图像视觉平衡度计算模型,改进了原有模型的左右平衡指标和上下平衡指标的计算,同时做了归一化处理,更加清晰地观察到地图图像的视觉平衡偏重情况(式(1))。
U = √(Ulr2 + Utb2)/√2
Ulr = (VMR - VML)/max(VML, VMR)
Utb = (VMT - VMB)/max(VMT, VMB)
式中:U为地图图像视觉平衡度的总体平衡指标;Ulr为地图图像视觉平衡度的左右平衡指标,Utb为地图图像视觉平衡度的上下平衡指标;VMR、VML、VMT、VMB分别为地图图面左、右、上、下4个部分所包含图面配置要素的视觉重力矩之和;max(VML/T, VMR/B)为2个部分视觉重力矩的较大值。
3.2.1 视觉重力矩
使用上述模型计算地图图像视觉平衡度指标的重点在于计算出地图图像中各个主图和各个图面辅助要素的视觉重力矩值。本文沿用了文献[8]提出的视觉重力矩函数模型(式(2))。
VGi = Si × ρi
vmi = VGi × Li
VMj = ∑i=1nvmi
式中:1 ≤ i ≤ n,n为地图图像中主图和图面辅助要素的总数;VGi为第i个要素的视觉重量;Si为第i个要素的面积;ρi为第i个要素的视觉密度;vmi为第i个要素的视觉重力矩;Li为第i个要素到地图图像中心的距离;VMj为地图图面左、右、上、下4个部分(j ∈ {L, R, T, B})所包含图面配置要素的视觉重力矩之和。
3.2.2 视觉密度
视觉密度是指地图图像中各个要素的视觉重量与面积的比值,是视觉重量的单位面积贡献率,其大小与要素的颜色、形状等特征有关。本文选取颜色、形状、位置3个因子进行视觉密度的计算,如式(3)所示。
ρi = wcρc + wsρs + wpρp
式中:ρi为第i个要素的视觉密度;ρc、ρs、ρp分别为颜色、形状、位置3个因子的视觉密度;wc、ws、wp分别为颜色、形状、位置3个因子的权重,且wc + ws + wp = 1。
(1)颜色因子。颜色因子的视觉密度与颜色的亮度、色相、饱和度以及颜色与背景的对比度有关。本文采用了RGB颜色空间下的颜色对比度计算方法,如式(4)所示。
ρc = √[(Ri - Rb)2 + (Gi - Gb)2 + (Bi - Bb)2]/√3
式中:Ri、Gi、Bi分别为第i个要素的红、绿、蓝三通道的颜色值;Rb、Gb、Bb分别为背景的红、绿、蓝三通道的颜色值;ρc的取值范围为[0, 1]。
(2)形状因子。形状因子的视觉密度与形状的复杂程度有关,形状越复杂,视觉密度越大。本文采用形状的周长与面积比来表示形状的复杂程度,如式(5)所示。
ρs = Pi/2√πSi
式中:Pi为第i个要素的周长;Si为第i个要素的面积;ρs的取值范围为[1, +∞),为了便于计算,本文对ρs进行了归一化处理,使其取值范围为[0, 1]。
(3)位置因子。位置因子的视觉密度与要素在地图图像中的位置有关,位置越重要,视觉密度越大。本文采用要素到地图图像中心的距离来表示位置的重要程度,如式(6)所示。
ρp = 1 - Li/Lmax
式中:Li为第i个要素到地图图像中心的距离;Lmax为地图图像中心到图像边缘的最大距离;ρp的取值范围为[0, 1]。
3.3 基于专家问卷的泛在地图图像视觉平衡度评价知识获取
为了获取泛在地图图像视觉平衡度的评价知识,本文采用专家问卷调查的方式,收集地图制图专家对泛在地图图像视觉平衡度的评价数据。
3.3.1 问卷设计
本文设计了一份泛在地图图像视觉平衡度评价问卷,问卷内容包括:
- 被调查者的基本信息,包括姓名、性别、年龄、职业、教育程度等;
- 被调查者的地图制图经验,包括地图制图年限、制图类型、制图工具等;
- 泛在地图图像视觉平衡度评价,包括对每幅地图图像的视觉平衡度评价,评价结果分为"平衡"、"难以区分"、"不平衡"3类。
3.3.2 问卷调查
本文采用互联网问卷调查的方式,向地图制图专家发放问卷。问卷调查的对象为具有地图制图经验的专业人员,包括地图制图教师、地图制图工程师、地图制图研究人员等。问卷调查的时间为2022年3月至2022年5月,共收集了30名地图制图专家对1 730幅泛在地图图像的视觉平衡度评价数据。
3.3.3 问卷数据处理
对收集到的问卷数据进行统计分析,得到每幅地图图像的视觉平衡度评价结果。本文采用多数表决的方式,将每幅地图图像的视觉平衡度评价结果确定为被调查者中占比最高的评价结果。同时,为了保证评价结果的可靠性,本文设定了评价结果的置信度阈值,即当某一评价结果的占比超过60%时,才将该评价结果作为地图图像的视觉平衡度评价结果,否则将该地图图像的视觉平衡度评价结果确定为"难以区分"。
3.4 基于贝叶斯决策的泛在地图图像视觉平衡度判别
基于地图图像视觉平衡度计算模型得到的视觉平衡度指标和专家问卷调查得到的视觉平衡度评价结果,本文采用贝叶斯决策方法对泛在地图图像的视觉平衡度进行判别。
贝叶斯决策是一种基于概率统计的决策方法,其核心思想是根据先验概率和条件概率计算后验概率,然后根据后验概率进行决策。本文采用最小错误率贝叶斯决策方法,即选择使得错误率最小的决策规则。
基于贝叶斯决策模型,本文将泛在地图图像的视觉平衡度判别为"平衡"、"难以区分"、"不平衡"3类。具体步骤如下:
- 计算地图图像的视觉平衡度指标Ulr、Utb和U;
- 根据专家问卷调查得到的视觉平衡度评价结果,将地图图像分为"平衡"、"难以区分"、"不平衡"3类;
- 估计各类别的条件概率密度p(x|ωi)和先验概率P(ωi);
- 对于一幅新的地图图像,计算其视觉平衡度指标,然后根据贝叶斯决策规则判别其视觉平衡度类别。
4 实验与分析
为了验证本文提出的泛在地图图像视觉平衡度计算框架的有效性,本文进行了一系列实验。
4.1 实验数据
本文通过互联网搜索引擎搜集了1 730幅泛在地图图像,包括各种类型的地图,如政区地图、交通地图、旅游地图、专题地图等。这些地图图像的来源广泛,包括政府网站、新闻媒体、社交媒体、学术论文等,具有较好的代表性。
对于每幅地图图像,本文采用人工标注的方式,从地图图像中提取主图和图面辅助要素,并确定这些要素在图像上的位置范围及要素类别。同时,本文通过专家问卷调查,获取了30名地图制图专家对这些地图图像的视觉平衡度评价数据。
4.2 实验设置
本文采用5折交叉验证的方式进行实验,将数据集随机分为5个子集,每次选择其中4个子集作为训练集,剩余1个子集作为测试集,重复5次实验,取平均值作为最终结果。
在视觉密度计算中,颜色、形状、位置3个因子的权重分别设为0.4、0.3、0.3。在贝叶斯决策模型中,假设条件概率密度服从多元正态分布,采用最大似然估计方法估计均值向量和协方差矩阵。
4.3 实验结果与分析
本文使用准确率(Accuracy)、精确率(Precision)、召回率(Recall)和F1值(F1-score)作为评价指标,评估泛在地图图像视觉平衡度判别的性能。
| 类别 | 准确率 | 精确率 | 召回率 | F1值 |
|---|---|---|---|---|
| 平衡 | - | 0.856 | 0.839 | 0.847 |
| 难以区分 | - | 0.792 | 0.804 | 0.798 |
| 不平衡 | - | 0.831 | 0.845 | 0.838 |
| 总体 | 0.8285 | 0.826 | 0.829 | 0.828 |
从表1可以看出,本文提出的泛在地图图像视觉平衡度计算框架在测试集上取得了82.85%的总体准确率,各类别的精确率、召回率和F1值均在0.79以上,表明该框架能够有效地判别泛在地图图像的视觉平衡度。其中,"平衡"类别的判别性能最好,F1值达到0.847;"难以区分"类别的判别性能相对较差,F1值为0.798,这可能是因为"难以区分"类别的样本特征分布更加复杂,与其他两个类别存在一定的重叠。
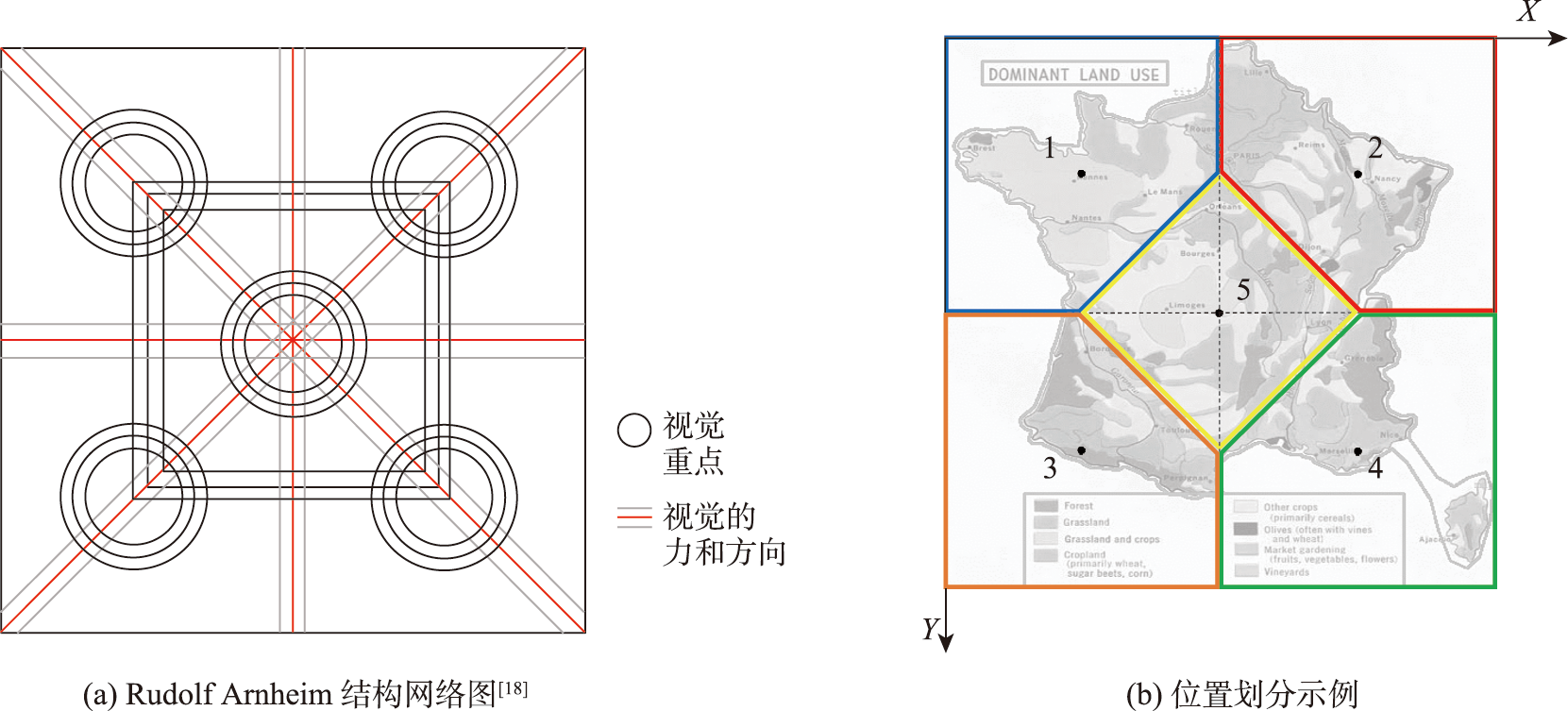
图3 不同视觉平衡度类别的地图图像示例
图3展示了不同视觉平衡度类别的地图图像示例。可以看出,"平衡"类别的地图图像(图3a)主图和图面辅助要素分布均匀,视觉重心接近地图中心;"不平衡"类别的地图图像(图3c)主图或图面辅助要素分布不均,视觉重心偏离地图中心;"难以区分"类别的地图图像(图3b)则介于两者之间,视觉平衡度不够明显。
4.4 对比实验
为了进一步验证本文提出的泛在地图图像视觉平衡度计算框架的有效性,本文将其与现有的几种地图视觉平衡度计算方法进行了对比,包括马俊等提出的基于力矩平衡原理的视觉平衡度计算模型(方法A)、魏智威等提出的基于视觉中心与理论视觉中心距离的视觉平衡度计算方法(方法B)以及徐建新等提出的基于灰度分布均衡的视觉平衡度计算模型(方法C)。
| 方法 | 准确率 |
|---|---|
| 方法A | 0.723 |
| 方法B | 0.685 |
| 方法C | 0.751 |
| 本文方法 | 0.829 |
从表2可以看出,本文提出的方法在泛在地图图像视觉平衡度判别准确率上明显优于其他方法。方法A和方法B的准确率相对较低,分别为0.723和0.685,这可能是因为它们考虑的影响因子较为简单,无法全面描述泛在地图图像的视觉平衡特性。方法C的准确率为0.751,相对较高,但仍低于本文方法,这可能是因为它虽然考虑了灰度分布均衡,但忽略了形状因子的影响,且对颜色因子的量化不够准确。本文方法通过丰富视觉密度影响因子,并引入贝叶斯决策模型学习专家评价知识,能够更加全面、准确地描述和判别泛在地图图像的视觉平衡度。
5 结论
本文提出了一种基于多因子贝叶斯决策的泛在地图图像视觉平衡度计算框架,通过结合地图图像计算特征与专家评价知识,实现了对泛在地图图像视觉平衡度复杂分布的有效判别。主要研究成果如下:
- 提出了一种基于力矩平衡原理的地图图像视觉平衡度计算模型,改进了左右平衡指标和上下平衡指标的计算,并做了归一化处理,使得视觉平衡度指标更加清晰直观。
- 丰富了地图视觉密度影响因子,选取颜色、形状、位置3个因子进行视觉密度计算,并对各因子进行了定量描述,使得视觉密度计算更加全面准确。
- 构建了泛在地图图像视觉平衡度评价数据集,收集了30名地图制图专家对1 730幅泛在地图图像的视觉平衡度评价数据,为泛在地图图像视觉平衡度研究提供了数据支持。
- 引入贝叶斯决策方法,基于地图图像视觉平衡度指标和专家评价知识,构建了泛在地图图像视觉平衡度判别模型,有效解决了人为主观判别地图视觉平衡度存在的不确定性问题。
实验结果表明,本文提出的泛在地图图像视觉平衡度计算框架在本文构建的泛在地图图像视觉平衡度评价数据集上能取得82.85%的评价准确率,明显优于现有的地图视觉平衡度计算方法。这说明该框架能够有效地判别泛在地图图像的视觉平衡度,为泛在地图图像的质量评价和筛选提供了有力工具。
本文的研究成果对于指导泛在制图过程中对于视觉平衡的把握,提高泛在地图图像的资源利用价值,促使泛在制图更符合地图设计规律具有重要意义。未来的研究方向包括:进一步丰富视觉密度影响因子,考虑更多的视觉变量;探索深度学习等人工智能技术在泛在地图图像视觉平衡度计算中的应用;扩展研究范围,将视觉平衡度计算扩展到其他类型的地图产品中。
引用格式
徐晔秋,杨剑,贾奋励,等.一种基于多因子贝叶斯决策的泛在地图图像视觉平衡度计算框架[J].地球信息科学学报,2024,26(1):184-196. [ Xu Y Q, Yang J, Jia F L, et al. A calculation of visual balance index of ubiquitous map images based on multi-factor bayesian decision making[J]. Journal of Geo-information Science, 2024,26(1):184-196 ] DOI:10.12082/dqxxkx.2024.220754
* 以上内容由AI自动生成,内容仅供参考。对于因使用本网站以上内容产生的相关后果,本网站不承担任何商业和法律责任。