近场动力学与深度学习相结合的地面沉降建模和模拟方法

摘要

【背景】近场动力学等物理模型方法具备无需先验知识与连续性假设的优势，已在地面沉降建模中得到一些应用。然而，此类模型方法的模拟精度受地下空间结构与边界条件等多方面因素的制约，地下水位变化、建筑静载荷以及道路动载荷等会对模拟结果产生显著影响。物理模型与深度学习存在天然的互补优势，二者的耦合是极具前景的发展方向，有望获取更为精确的模拟结果。

【方法】本文提出了一种将基于近场动力学的物理模型与深度学习相结合的地面沉降建模和模拟方法，在利用近场动力学描述区域地面沉降物理过程的基础上，采用神经网络和高斯过程回归的深度学习方法，构建符合时序发展变化的各类边界条件信息，实现近场动力学地面沉降模型的边界条件优化。

【结果】通过对2021年9月—2023年5月北京市通州区实验区地面沉降的建模与模拟，结合深度学习的近场动力学地面沉降模型的训练集、测试集模拟结果RMSE分别为6.25 mm、7.71 mm，比未使用高斯过程回归方法的模拟结果RMSE（22.62 mm）减少了72.37%、65.92%。

【结论】实验表明，近场动力学与深度学习相结合的地面沉降建模与模拟方法能够显著提高沉降结果精度，物理模型与人工智能相结合的思路与方法在区域地面沉降研究中具有良好的适用性与应用前景。

近场动力学物理模型深度学习地面沉降建模参数优化

研究亮点

物理模型与深度学习的创新结合

提出了一种将近场动力学物理模型与深度学习方法相结合的创新思路，实现了物理机制与数据驱动的互补优势。

显著提升的预测精度

结合深度学习的近场动力学模型使预测误差减少了65%以上，特别适用于地层结构复杂、沉降差异性明显的区域。

边界条件的智能优化

通过神经网络和高斯过程回归方法，实现了地下水位变化、建筑静载荷和道路动载荷等边界条件的智能优化。

广泛的应用前景

该方法在区域地面沉降研究中展现出良好的适用性，为城市规划、地质灾害预防等领域提供了有力支持。

引言

近年来，地球科学领域正经历从信息稀缺到信息丰富的转变，大数据时代获取和生成地学时空数据的能力已经远远超过了处理、分析和理解这些数据的能力。在此背景下，以机器学习（Machine Learning，ML）和深度学习（Deep Learning，DL）为代表的人工智能（Artificial Intelligence，AI）技术迅猛发展，在解决地球科学相关问题方面已显示出前景，在遥感与数值模拟领域受到广泛关注和快速发展。

与浅层机器学习算法相比，深度学习具有多个隐层节点，更能学习到重要的特征，从而提升模型准确性。深度学习在地球系统科学中的机遇与挑战并存，一方面，深度学习在地学中的应用还处于初级阶段，在定量应用方面被广泛应用于特征参量的遥感反演，也被成功应用于大气和水文等地表过程的模拟预测，表现出很大的应用潜力；另一方面，在针对机器学习的地学应用研究中，鉴于地学过程具有复杂性、交互性以及多尺度特性，同时又存在数据的不确定性和真实样本的稀缺性等问题，深度学习目前仍然无法完全取代物理模型。

物理模型与深度学习的耦合是"理性主义"与"经验主义"的结合，将成为地球科学研究发展的"助推器"。物理模型通常基于物理规律和机制，而深度学习可以从大量数据中学习模式，考虑到物理模型可靠的外推能力和深度学习强大的拟合能力，两种模型具有天然的互补优势。物理模型与深度学习的耦合关系可以被归纳为3类基本范式：机理级联学习、机理融进学习、学习嵌入机理。

地面沉降是一种由于自然因素或人类工程活动等多种复杂因素引发的地下松散岩层固结压缩，并导致一定区域范围内地面高程降低的地质灾害。当前地面沉降问题愈加突出，其复杂性、危险性与不确定性加强，已广泛影响全球150多个国家和地区。

为此，本文在当前基于近场动力学的地面沉降建模研究基础上，提出了近场动力学和深度学习相结合的地面沉降建模与模拟方法。一方面利用近场动力学理论描述地面沉降的物理过程，另一方面利用深度学习方法对近场动力学地面沉降模型中的重要参数和边界条件进行优化，从而提高区域地面沉降模拟的效率和精度。本研究为区域地面沉降建模与模拟预测提供了新思路，为深度学习嵌入物理模型范式拓展了新应用场景。

研究思路与方法

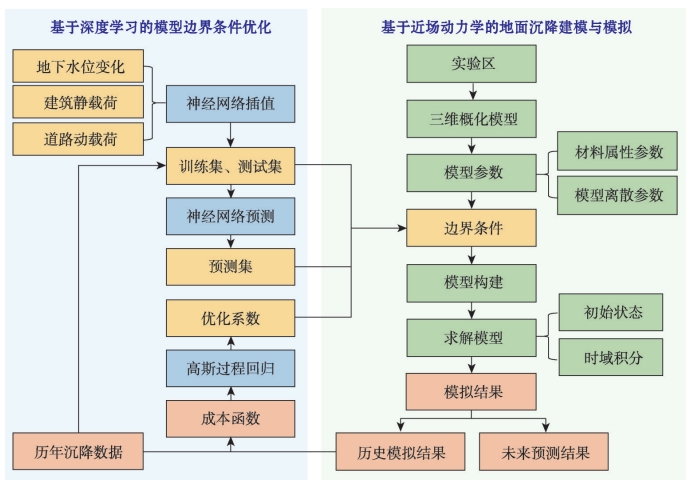
图1 近场动力学与深度学习相结合的地面沉降建模与模拟流程

近场动力学与深度学习相结合的地面沉降建模与模拟的方法流程如图1所示。首先，基于近场动力学理论，构建近场动力学地面沉降模型。近场动力学地面沉降模型的模拟精度受地下空间结构和边界条件等多方面影响。其中，地下水位变化、建筑静载荷及道路动载荷等边界条件会对模拟结果造成显著影响。因此，采用神经网络插值方法处理逐月地下水位变化等边界条件数据和历年沉降监测数据，并划分为训练集（Training Set）和测试集（Test Set），再使用神经网络模型生成未来边界条件预测集（Prediction Set），最后通过高斯过程回归方法优化模型边界条件系数。

2.1 基于近场动力学的地面沉降模型构建

2000年Silling提出了近场动力学的基本思想，称为键型理论。2007年Silling等将键型理论扩展为态型理论，对近场动力学进行了完善。近场动力学基于非局部建模思想，通过空间积分对微观与宏观力学作用进行统一描述，能够应用于非连续应力场与形变场的模拟与预测。在某时刻t，对于占据空间区域R的物质体，常规态型近场动力学方程公式如下：

ρü(x,t) = ∫_Hx{-T[x,t]^x'-x-T'[x',t]^x-x'}dV_x' + b(x,t)

式中：ρ为材料密度；ü代表物质点x在时刻t下的加速度；Hx表示以物质点x为中心且邻域半径δ划定的近场范围；-T为力状态矢量，由与物质点x相关的所有力密度矢量组成；b为施加在物质点x上的体积力密度矢量。等式左边两项乘积表示物质体所受合外力。

2.2 神经网络支持下的模型边界条件建立

克里金法和反距离权重法等传统空间插值技术会受主观假设以及预设公式的限制，并不一定适用于非线性的现实世界情况。为克服这些限制，通过神经网络插值方法生成各类外载荷信息的空间格网数据集，从而建立模型边界条件。

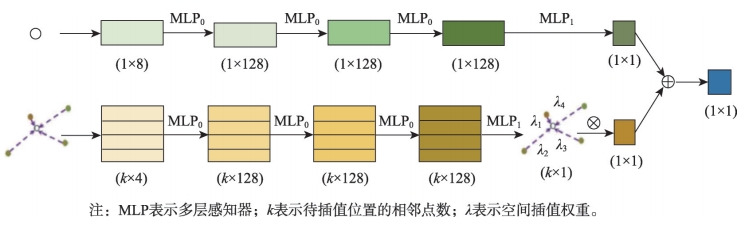
图2 神经网络插值结构示意图

神经网络插值结构如图2所示，模型分为上下2个子模型，上部分模型网络用于φ的估算，上层网络的输出首先经过3层MLP0，每层MLP0由一个线性变换函数、一个层归一化函数和一个非线性激活函数ReLU组成，最后在第4层通过线性变换得到参数φ(v_l0)。下部分模型网络用于ψ的估算，网络结构与上部分模型基本一致，但在第5层与各个已知点的数据做乘积，直接得到∑ψ(d_l0,li)·Z(l_i)。最后将2部分模型得到的结果相加即为最终预测的边界条件值。

2.3 基于高斯过程回归的模型边界条件优化

高斯过程回归（Gaussian Process Regression，GPR）是使用高斯过程（Gaussian Process，GP）对数据进行回归分析的非参数模型，是一种基于贝叶斯理论和统计学习方法的监督学习类算法。结合高斯过程回归，针对边界条件系数θ的优化思路是通过一段时间T内的模拟值与监测值的时间序列和贝叶斯规则，得到系数θ的后验概率分布p(θ|y₀^T)。

实验与结果分析

3.1 实验区地面沉降建模

3.1.1 实验区概况与数据源

通过综合考虑地面沉降、地下水降落漏斗、城市与农村空间分布特征等因素，在北京市通州区选取差异性沉降的典型实验区，如图3所示。实验区中轴线的起点为凉水河左堤路与国道103的交叉口，然后以东南-西北走向沿国道103穿过东六环，沿途经过了农村与城市用地，直至梨园中街与玉桥中路的交叉口。

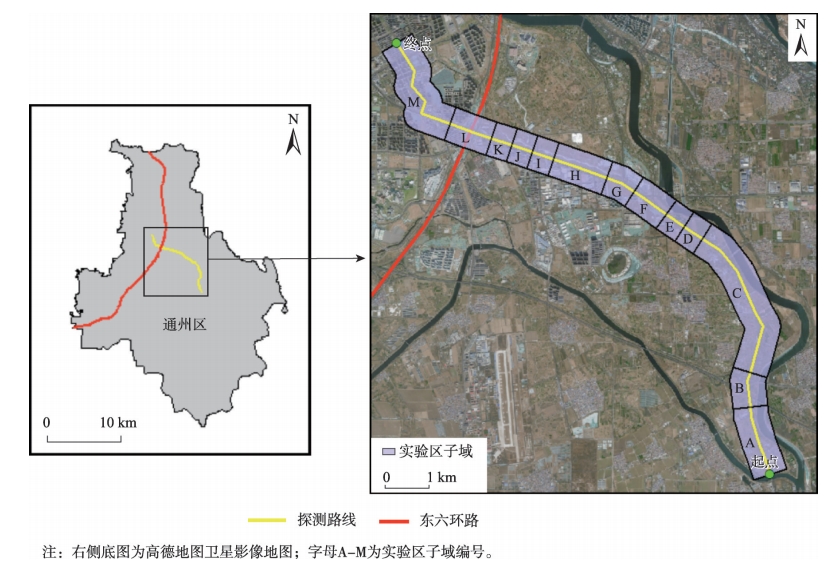
图3 北京市通州区实验区与SFRT探测路线

3.1.2 模型构建与参数确定

水文地质系统是由不同等级、不同类型的水文地质综合体和地下水体所构成的有机整体。开展区域地面沉降模拟研究首先需要分析区域水文地质体的系统、组分与外部环境，构建区域水文地质结构的模型。根据复杂系统和多体理论，基于SFRT数据，构建实验区水文地质的三维概化模型并进行离散。

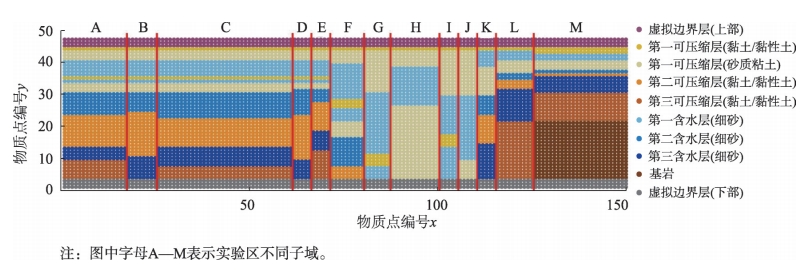
图4 实验区模型结构剖面图

3.2 实验区地面沉降模拟

3.2.1 边界条件与模拟结果

按照本文近场动力学与深度学习相结合的地面沉降模拟方法，根据T1—T17训练集的逐月地下水位变化以及建筑静载荷、道路动载荷等边界条件数据，结合InSAR沉降监测数据。

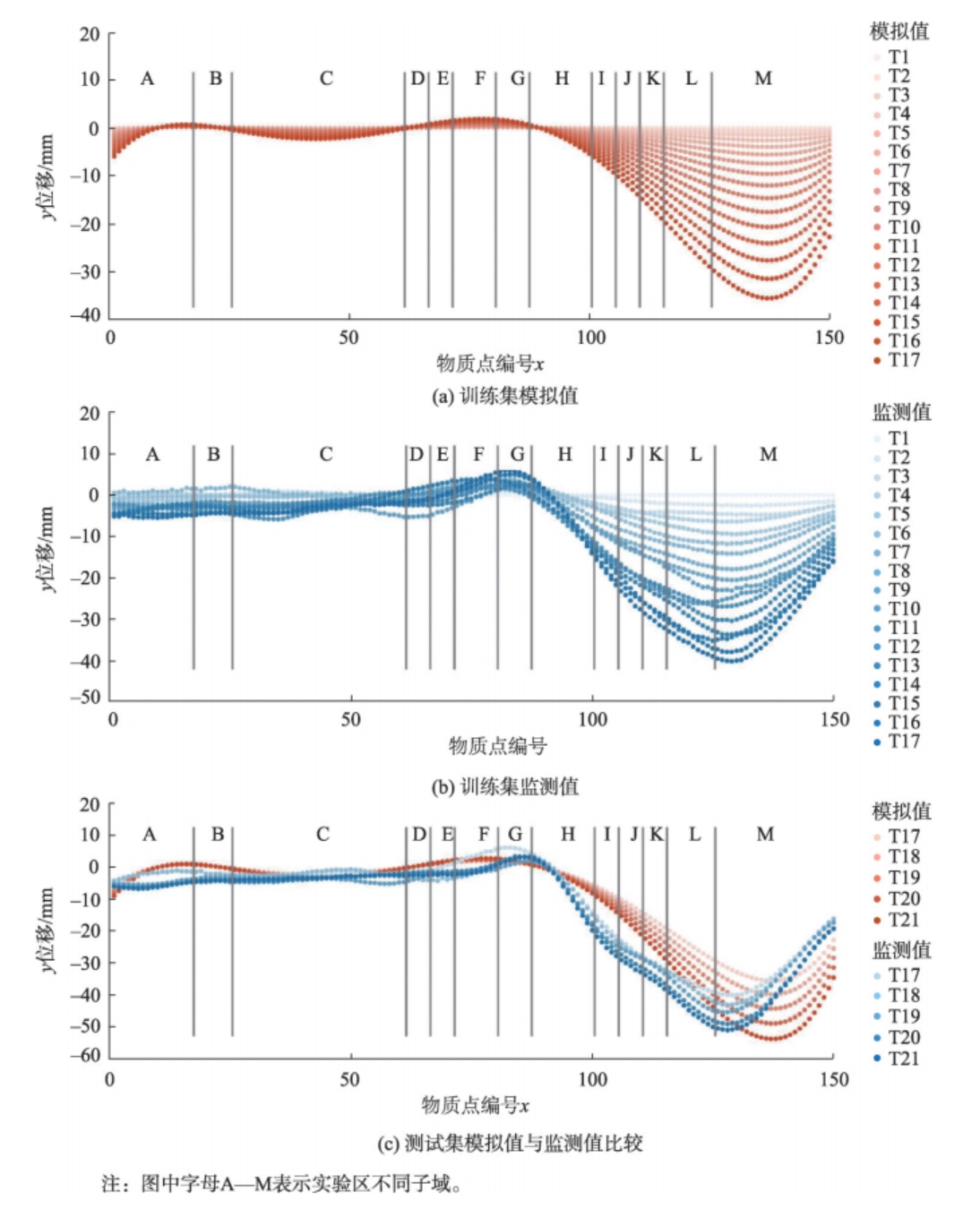
图5 训练集与测试集模拟结果

3.2.2 精度评价与结果分析

选择RMSE作为衡量模拟结果与监测值之间偏差的指标，RMSE越小，说明偏差越小，模拟效果越好。如表3所示，依据本文方法模拟得到的训练集整体RMSE为6.25 mm，测试集整体RMSE为7.71 mm；而当使用未经高斯过程回归优化的边界条件系数时，近场动力学地面沉降模型的整体RMSE为22.62 mm。本文方法的训练集、测试集模拟结果整体RMSE相较于未使用高斯过程回归方法分别减少了72.37%和65.92%，充分说明本文方法能够有效提高地面沉降模拟精度。

实验结果表明，近场动力学地面沉降模拟结果精度受到地下水位变化、建筑静载荷、道路动载荷等边界条件影响，通过合适的边界条件系数取值，近场动力学地面沉降模型能够得到较好的沉降模拟演化结果。尤其在地层结构复杂、可压缩层厚度差异大的区域，本文方法模拟结果与监测值的时序趋势较为接近。本次实验初步验证了深度学习方法和近场动力学相结合，在地面沉降建模以及边界条件优化研究中的实用性和有效性。

结论

为优化当前近场动力学地面沉降模型的模拟精度和效果，本文利用近场动力学描述区域地面沉降物理过程，同时采用神经网络和高斯过程回归的深度学习方法，开展近场动力学地面沉降模型边界条件建立和优化的研究。主要工作如下：

依据近场动力学理论，在确定研究对象的空间结构、相关参数及边界条件后，构建近场动力学地面沉降模型；
采用神经网络插值方法处理逐月地下水位变化等边界条件数据和历年沉降监测数据，并划分为训练集和测试集；
鉴于地下水位变化、建筑静载荷与道路动载荷的边界条件系数存在空间异质性问题，通过高斯过程回归方法对模型边界条件系数进行优化；
通过模拟2021年9月—2023年5月北京市通州区实验区地面沉降过程，本文方法的训练集、测试集结果RMSE比未使用高斯过程回归方法减少了72.37%、65.92%，这表明了本文方法能够有效提高地面沉降模拟精度，适用于地层结构复杂、可压缩层厚度差异大的区域。

本文初步验证了耦合物理模型与人工智能的思路和方法在区域地面沉降研究中的可行性和实用性，但还存在一些不足，如未充分考虑边界条件系数的时空变异性、忽略地面沉降对地下水位变化响应的滞后性以及训练时间序列过短等。后续研究将考虑扩展模型时间序列，针对边界条件系数的时空变异性、地下水位变化与地面沉降之间的滞后性等问题展开更为深入的研究。