面向地下场景的超宽带导航完好性保护级算法改进

研究背景

地下导航的挑战

随着导航定位技术的发展和导航应用场景需求的增加，导航定位从航空逐渐走向室内和地下等多方位场景，向着更精确、更可靠的方向发展。为解决室内/地下环境卫星信号弱的问题，Wi-Fi、蓝牙、红外线、动作捕捉和超宽带等各种室内定位技术应运而生。

其中，超宽带（UWB）定位技术通过发送和接收极窄脉冲来传输数据，与传统的窄带系统相比，具有穿透力强、抗多径干扰效果好、定位精度更高等优点，在城市轨道交通、隧道及地下大空间这类非暴露空间有着广泛的用途。随着智慧城市与新基建的发展，不仅需要引入地下空间的精准定位技术，还对非暴露空间定位的可靠性提出了更高的要求，地下大空间定位完好性的研究显得更加迫切。

完好性与保护级概念

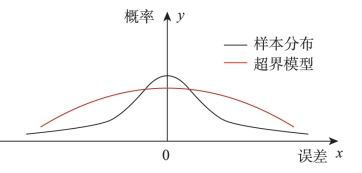
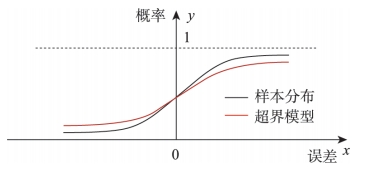
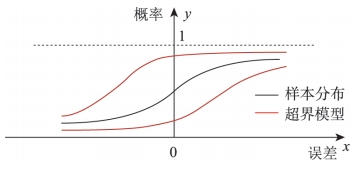
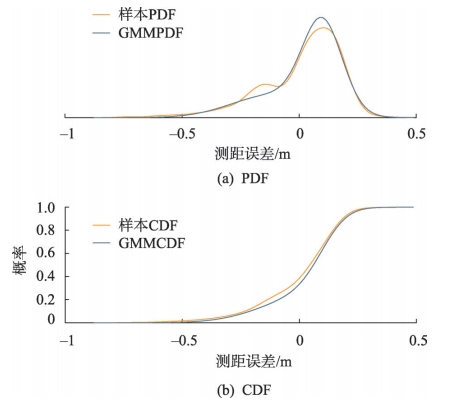
完好性的概念最初由全球卫星导航系统（GNSS）提出，是评价导航安全性的代表性指标。GNSS采用超界（Overbound）的典型保守方法来保障完好性，通常选用高斯参数模型代替真实误差的分布。扩大高斯分布的方差以确保实际误差的尾部被覆盖，这种方法被称为高斯超界。

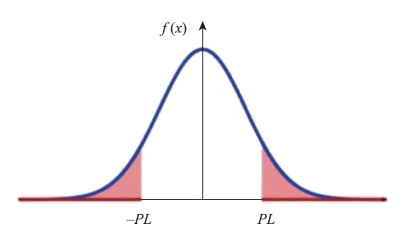
高斯PDF假设下PL和完好性风险之间的关系示意

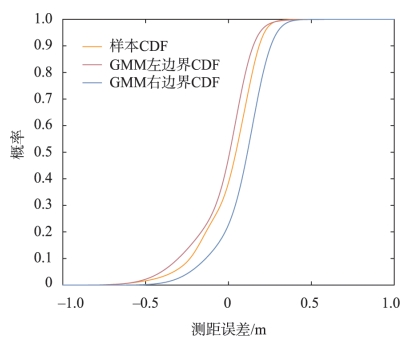
超界的累积尾部概率超过了真实分布的尾部概率，这种保守性可以通过线性系统传递到位置误差模型输出。对于无故障条件下的任何完好性风险，对应的所有分位数都大于真实误差的分位数。完好性风险所对应的分位数也被称为保护级（PL），这是确保完好性的关键测试统计数据。

现有方法的局限性

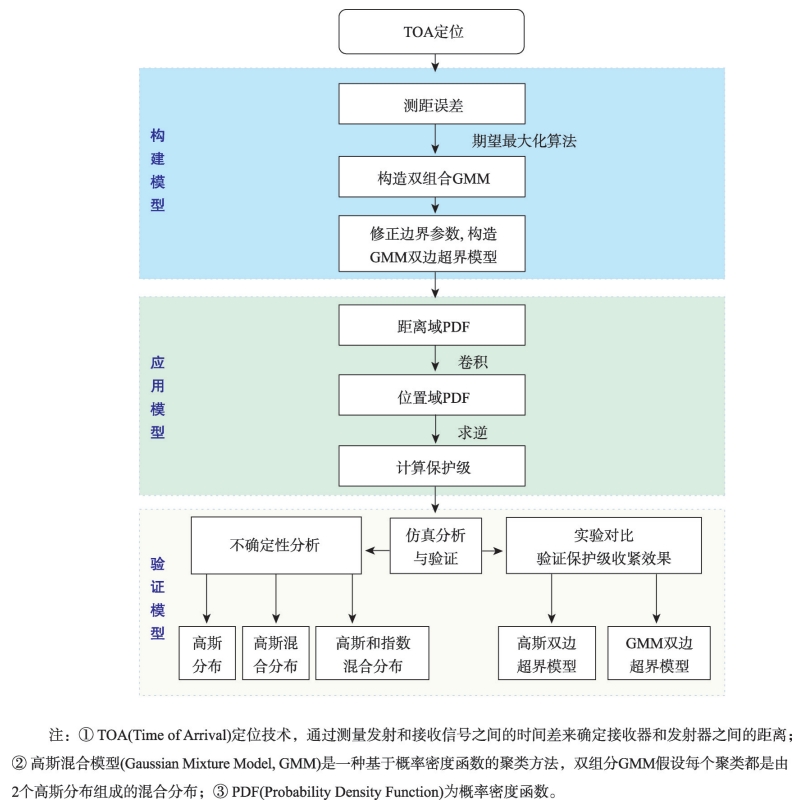
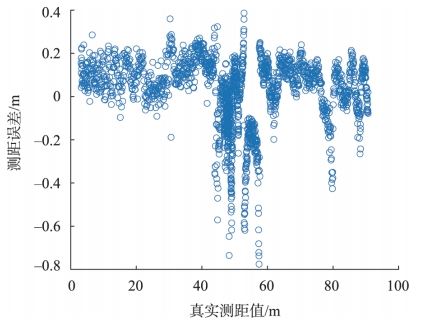
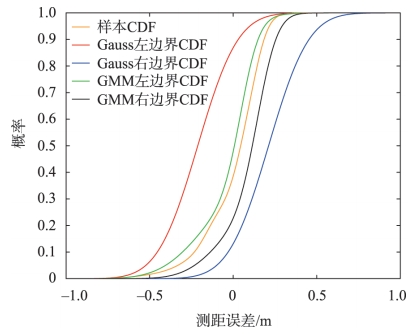
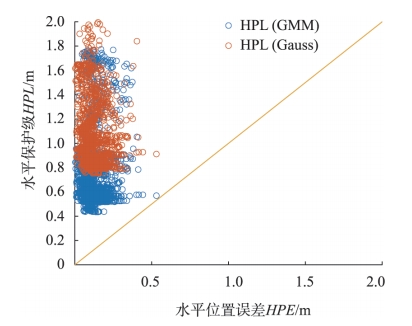
UWB系统的TOA定位原理与GNSS系统类似，但其误差特性相较于GNSS却有很大差异。地下大空间的UWB系统测距误差可能呈现非高斯特征，而GNSS系统则普遍采用零均值的高斯分布来包络误差。采用传统的超界方法来计算UWB系统的保护级是过于松散和保守的，可能导致系统可用性的下降。

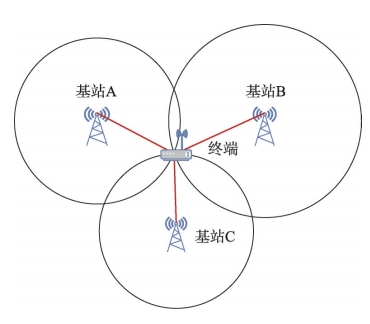
TOA定位模式示意图

与此同时，航空领域建立的关于电离层、对流层的误差模型在地下环境中也不再有效，所以GNSS完好性框架并不完全适用地下大空间的完好性评估体系。为满足复杂环境和特定场景下的应用需求，研究人员提出了各种超界(Overbounding)模型，对实际误差分布的尾部进行覆盖。

传统的误差超界模型

尾部超界

完好性要求所建立的误差模型比实际分布具有更大的尾部概率，从而使计算出的PL大于完好性风险下实际误差分布的分位数。

PL_o = |G^-1_o(P_HMI)| ≥ PL_a = |G^-1_a(P_HMI)|

尾部超界与完好性要求一致，即令超界函数在其尾部包含比实际分布更多的概率，以确保超界参数计算的保护级的结果大于对应的百分位数。但尾部超界方法仅在特定点定义，只能保证超界性质在这一点上是有效的。

PDF超界

为了解决尾部超界只能在某一点建立的问题，提出了PDF超界方法，定义在概率密度函数（PDF）的一段区间上。

g_o(x) ≥ g_a(x), ∀|x| > AL

PDF超界示意图

CDF超界

为了确保卷积运算后保守性仍然有效，有必要在变量x的整个值范围内进行定义。CDF超界方法同时考虑了上述两个要求。

G_o(x) ≥ G_a(x), ∀G_a < 1/2
G_o(x) < G_a(x), ∀G_a ≥ 1/2

CDF超界示意图

双边超界

双边超界方法改进了限制于单峰对称分布的CDF超界方法，允许任意形式的误差分布。

G_L(x) ≥ G_a(x), ∀x
G_R(x) ≤ G_a(x), ∀x

双边超界示意图

关键问题：以上超界方法均基于高斯分布，然而高斯包络的核心远大于实际误差分布的核心，由此计算得到的保护级是过于宽松和保守的，在系统可用性方面缺少保障，难以适应地下大空间的复杂场景。在距离域中对单个传感器的误差进行建模可更加灵活。基于此，本文从超界函数与实际误差分布之间的关系出发，对传统基于高斯分布的双边超界方法进行了改进。

基于GMM双边超界模型的保护级计算

技术路线

本文基于TOA定位模式，提出一种基于GMM的测距误差框架，能够更紧密地包络TOA测距误差，适应地下大空间的复杂场景。技术路线主要包括构建模型、应用模型、验证模型3部分。

超宽带导航系统计算保护级技术路线

构建模型

根据测距误差样本构造双组分GMM形式的概率密度模型并修正边界参数以获得GMM双边超界模型

应用模型

应用该超界模型提出计算保护级PL的方法

验证模型

开展实验进行评价与分析

构建GMM双边超界模型

为了解决高斯分布在处理重尾特性时过于保守的问题，选择GMM来拟合距离误差分布具有以下好处：

GMM是高斯函数的线性组合，多组分GMM甚至可以接近任意可积分布，能够准确刻画误差分布
GMM具有良好的卷积性质，卷积后仍保留了GMM形式，便于在位置域上直接分析误差分布

使用双组分GMM，以期最大限度地减少组分的数量，并且提供足够的灵活性。一组分用于描述核心，另一组分用于描述尾部。

f_a(x) = ω₁·G(x; μ₁, σ₁) + ω₂·G(x; μ₂, σ₂)

其中ω₁、ω₂分别为各组分的权重，并且满足ω₁+ω₂=1；μ₁、μ₂为各组分的均值；σ₁、σ₂为各组分的方差。以上参数可通过期望最大化（Expectation Maximum，EM）算法迭代给出。

双边超界条件

由于距离域PDF的尾部超界性质无法通过卷积传递到位置域，所以在距离域建模并不关心基于PDF的指标，而是基于CDF调整边界参数，又因样本分布通常不满足单峰对称条件，故采用CDF双边超界。双边超界只需满足条件：

F_L(x) > F_a(x), ∀x
F_R(x) < F_a(x), ∀x

左右边界函数的具体表达式为：

f_L(x) = (ω₁ + Δω)·G(x; μ₁ - Δμ, σ₁ + Δσ) + (ω₂ - Δω)·G(x; μ₂ - Δμ, σ₂)
= ω₁^L·G(x; μ₁^L, σ₁^L) + ω₂^L·G(x; μ₂^L, σ₂^L)

f_R(x) = (ω₁ - Δω)·G(x; μ₁ + Δμ, σ₁) + (ω₂ + Δω)·G(x; μ₂ + Δμ, σ₂ + Δσ)
= ω₁^R·G(x; μ₁^R, σ₁^R) + ω₂^R·G(x; μ₂^R, σ₂^R)

计算保护级PL

保护级PL是衡量位置域误差大小的重要指标，负责提供当前时刻的定位误差上界。首先将距离域误差转换到位置域上，距离域误差可以经空间投影转换得到位置域的定位误差：

e_q = ∑_i=1^N S_q,i·ε_k

其中，在平面定位场景，下标q代表水平方向上的位置分量，q=1代表X方向，q=2代表Y方向。S为空间几何投影矩阵；S_q,i表示第q行第i个元素；N为用户当前可用基站数，ε为距离域误差，e为位置域误差。

距离域超界PDF的参数均取超界更新后的值。将各基站的距离域误差映射到位置域，得到各基站对应的双边PDF。假设各基站的测量是独立的，对来自N个基站的位置域PDF进行连续卷积积分，容易得到位置误差PDF。

由PDF进一步积分即可得CDF表达式。将q方向的双边CDF记为F_q,L、F_q,R，对双边CDF各自求逆，求完好性概率P_HMI所对应的分位数，并取左右边界分位数中绝对值最大者为保护级。

水平保护级HPL是PL的水平分量，平面定位主要关注HPL，位置域HPL可表示为：

HPL = √(XPL² + YPL²)

仿真分析与验证

数据来源及实验设计

实验数据为2023年8月31日在地下模拟场景观测获得，以高精度惯导作为参考真值，使用6个UWB基站，采用TOA模式进行定位。实验流程包括：

基于UWB测距误差构建GMM超界模型
以其中一个基站为例，连续采集3~93 m范围内的1950个UWB测距数据
使用该测距误差样本数据进行GMM超界模型的构建
基于该GMM超界模型计算保护级，并与传统高斯双边超界方法计算的保护级进行对比
进行不确定性分析，将实验的样本数据替换成其他分布形式的仿真数据进行分析验证

GMM双边超界模型的参数估计

本文采用的样本数据在地下模拟场景观测获得，部分观测数据存在遮挡，模拟了地下可能存在的复杂环境。测量范围为3~93 m，共采集1950个历元的观测信息。

3~93 m范围内的测距误差散点图

用双组分GMM模型来刻画测距误差分布，其概率密度函数(PDF)表达式为：

f_a(x) = 0.352·G(-0.113, 0.176) + 0.648·G(0.096, 0.087)

其中第一组分权重为0.352，均值为-0.113 m，方差为0.176 m；第二组分权重为0.648，均值为0.096 m，方差为0.087 m。以上混合PDF的参数通过普遍接受的EM算法迭代给出。

模型效果验证

样本分布及GMM分布的PDF和CDF

EM算法给出的高斯混合模型与样本数据的吻合度较高，概率密度模型的构建较为合理。但超界模型对于边界有更高的要求，需要适当调整参数以满足左右边界条件。

GMM超界模型与样本数据的CDF

超界性能定量比较

对于距离域超界性能的定量比较，引入了差值总和（SUMD），基于CDF来描述分布之间的差异。将差值总和定义为：

SUMD = (1/N_bin)∑_i=1^N_bin|F_OB(x_i) - F_a(x_i)|

超界模型	参数	差值总和(SUMD)
GMM双边超界	ω₁^L = 0.397, σ₁^L = 0.212, μ₁^L = -0.162 ω₂^L = 0.603, σ₂^L = 0.085, μ₂^L = 0.049	0.028
GMM双边超界	ω₁^R = 0.297, σ₁^R = 0.177, μ₁^R = -0.062 ω₂^R = 0.703, σ₂^R = 0.093, μ₂^R = 0.149	0.060
高斯双边超界	σ_L = 0.189 6, μ_L = -0.183 3	0.156
高斯双边超界	σ_R = 0.189 6, μ_R = 0.183 3	0.147

样本数据与不同超界模型的CDF

GMM双边超界方法比传统的高斯双边超界方法更接近样本分布。因此，与传统高斯的双边超界方法相比，改进的GMM双边超界方法更能体现原始分布的趋势。

位置域误差和保护级

本文采用多基站TOA定位模式，主要考虑平面定位，基站数目为6个。小车在停车场作带转角的直线运动。

基站布局和小车运动轨迹

以高精度惯导作为参考真值，实验测得水平位置误差（HPE）集中在0.2 m左右。GMM双边超界和高斯双边超界这2种方法计算保护级的对比结果如下：

应用GMM双边超界模型和高斯双边超界模型对应的HPL

GMM双边超界方法计算的HPL集中在0.4~1.8 m，高斯双边超界方法计算的HPL集中在0.8~2.0 m。可见使用GMM双边超界方法计算的HPL比高斯双边超界方法降低了至少20%以上，更贴近真实的位置误差，有效降低了保守性，提高了系统的可用性。

不确定性分析

从理论上分析，不确定性主要来自小样本量和模型误差。当样本量足够大时，经验分布函数以全概率收敛于CDF，而少量样本的经验分布可能与实际的基本分布不完全相同。模型误差主要取决于所构建的模型对样本的逼近程度。

通过停车场的实测样本数据已验证双组分GMM对该组样本的刻画较为准确，并且GMM双边超界模型对于收紧保护级具有较好的效果。此外，还分别对单高斯分布、高斯混合分布、高斯和指数混合分布这3种形式的仿真数据进行了分析，以验证本文所提方法对不同样本数据的效果。

样本分布	参数
高斯	μ = 0，σ = 0.2
高斯混合	组分1(高斯)：ω₁ = 0.2, μ₁ = 0.5, σ₁ = 0.2 组分2(高斯)：ω₂ = 0.8, μ₂ = -0.2, σ₂ = 0.1
高斯和指数混合	组分1(高斯)：ω₁ = 0.3, λ = 4 组分2(指数)：ω₂ = 0.7, μ = 0, σ = 0.1

样本分布	高斯双边超界模型的差值总和(SUMD)		GMM双边超界模型的差值总和(SUMD)
样本分布	左边界	右边界	左边界	右边界
高斯	0.008	0.018	0.009	0.013
高斯混合	0.112	0.192	0.034	0.035
高斯和指数混合	0.134	0.165	0.049	0.042

从不同样本分布的SUMD指标对比可以看出，对于高斯分布的样本，GMM双边超界模型与高斯双边超界模型的效果相当；而对于非高斯分布的样本，GMM双边超界模型的SUMD指标明显小于高斯双边超界模型，说明GMM双边超界模型能够更好地逼近非高斯分布，从而更有效地收紧保护级。

结论

本文针对地下大空间超宽带导航系统的完好性保护级计算问题，提出了一种基于高斯混合模型的双边超界方法。主要研究成果如下：

双组分GMM建模

基于EM算法构建双组分GMM概率密度函数，更精确地刻画地下场景超宽带测距误差的重尾特性。

双边超界模型

通过调整GMM参数，构建满足双边超界条件的距离域误差模型，确保超界性质在卷积后仍然成立。

保护级计算

基于GMM双边超界模型推导位置域保护级计算方法，有效降低保守性，提高系统可用性。

通过实验验证，在地下模拟场景中，基于GMM双边超界模型计算的水平保护级比传统高斯双边超界模型降低了20%以上，更贴近真实的位置误差。不确定性分析表明，对于非高斯分布的样本，GMM双边超界模型能够更好地逼近实际分布，从而更有效地收紧保护级。

本文提出的方法不仅适用于超宽带导航系统，还可以推广到其他具有非高斯误差特性的导航系统，如超声波、伪卫星及多源融合导航系统等。未来的研究方向包括：

考虑多组分GMM模型，进一步提高对复杂误差分布的拟合精度
探索自适应调整GMM参数的方法，以适应不同场景下的误差特性变化
结合故障检测与排除技术，提高系统在存在异常测量的情况下的完好性保障能力