1 引言
随着城市化进程的加速和人们生活水平的提高,城市中人口和车辆的数量不断增加,导致城市交通系统面临着巨大的压力。智能交通系统(ITS)通过运用各种高新技术,系统地解决道路交通问题,而其核心就在于实时且准确的交通预测。基于历史时刻的交通速度数据进行未来交通信息的预测,不仅有助于缓解交通拥堵,还对城市的可持续发展具有重要意义。因此,如何从复杂多维的交通数据中提取时空特征,并实现端到端的一体化预测,已成为当下研究热点。
现有的交通预测方法包括数理统计方法、机器学习方法和深度学习方法。传统的数理统计方法包括自回归差分移动平均模型(ARIMA)、卡尔曼滤波等。这些方法结构简单,计算成本低,但都依赖于数据的稳定假设,与实际非稳定的交通数据不符。此外,这类统计模型对先验知识具有强依赖性,难以有效建模交通速度数据的时空变化。基于机器学习的算法如支持向量机(SVM)等能够从复杂的交通速度数据中学习到交通变化规律,但是对于数据的时空特性挖掘效果较差,难以学习到空间依赖关系。传统的数理统计方法和机器方法大多适用于单一时间序列预测问题,没有考虑到数据的空间依赖性,无法满足多元预测的复杂条件,难以有效结构化交通数据中的时空关系。
深度学习技术中,循环神经网络(RNN)、卷积神经网络(CNN)等在非线性关系捕捉和预测精度方面具有显著优势,被广泛应用于交通速度预测任务。RNN及其变体LSTM、GRU等沿着时间维度逐步处理数据,在深层次挖掘交通数据的时间特征方面取得了良好的预测效果,但难以捕获交通数据的空间关联特征,并且迭代训练的过程也会导致误差累积,对时间和内存的消耗大。CNN在欧式数据上表现出较好的特征捕捉能力,因而被引入交通预测领域以增强模型对空间特征的挖掘能力。然而,CNN对空间特征的挖掘依赖于欧式空间网格数据,难以直接处理非欧式的图数据。
研究创新点
本文提出了一种基于多元时间序列动态图神经网络(MTDGNN)的交通速度预测方法。该方法将道路网络中的交通信息视为多元时间序列,每个路段被视为一个节点。通过设计一个融合动态交通信息与静态路网拓扑的图学习模块,实现了动态自适应邻接矩阵的生成。
2 多元时间序列动态图神经网络(MTDGNN)模型
本文构建的MTDGNN模型,根据实时交通状况和交通网络拓扑结构,从数据中提取特征,生成动态自适应图,以反映交通节点之间的动态空间关联。进一步采用混合时间卷积和空间卷积层,提取交通速度数据的动态时空特征,实现对城市道路的交通预测。
具体来讲,MTDGNN模型包括图学习层、图卷积模块、时间卷积模块以及一个输出模块。图学习层从已有数据中动态自适应地学习图结构,并将学习到的图与输入的预定义图一起作为图卷积模块的输入。图卷积模块和时间卷积模块分别用于挖掘节点之间的空间依赖关系和提取时间特征,两种模块采用交错叠加的方式以同时捕捉时空依赖性,避免时间依赖和空间依赖的过度分离,使每个卷积层都能通过空间和时间的双重信息进行调整。同时,为了避免梯度消失,模型加入了残差连接和跳跃连接。跳跃连接贯穿整个模型,将跨层的特征直接连接到后续模块,允许模型同时利用不同层级的特征;残差连接是局部模块内部的连接机制,将模块的输入直接加到模块的输出中,帮助优化梯度流,提升深层网络的训练效率。最后,输出模块将隐藏的特征投影到所需要的维度,并对预测结果进行评估与输出。
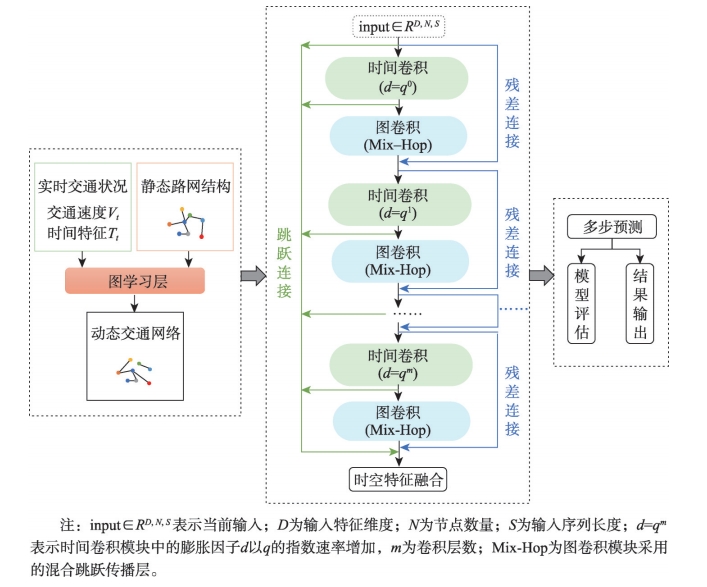
图1 MTDGNN模型框架
2.1 图学习层
对城市道路未来交通状况的预测,需要同时考虑到路网结构和当前交通状况。城市道路交通往往比较复杂,道路节点之间的关联在空间上有固定拓扑,在时间上呈动态演化,对静态、动态的双重邻接信息都具有强烈要求。在静态路网结构的基础上,实时交通信息的变化会导致道路节点之间的关联关系动态调整。
为了可以有效识别交通路网中节点之间潜在的动态空间关联,本文设计了一个基于神经网络的图结构学习模块。该模块通过一种基于GNN的超网络,从实时交通信息中提取数据特征,并结合静态和动态信息来生成动态滤波张量。动态滤波张量用于动态学习和调整邻接矩阵,确保图结构能反映当前的交通状态。随后,将学习到的动态滤波张量应用于随机初始化的节点嵌入,生成动态的节点嵌入。通过计算各动态节点嵌入之间的相似性度量,构建动态邻接矩阵,作为之后图卷积模块的动态图输入。
2.2 图卷积模块
交通网络中各路段的交通速度不仅受自身影响,还受网络中其他节点交通情况的影响,图卷积能够有效捕捉各路段间复杂的空间交互关系。具体而言,图卷积模块通过整合预定义的静态邻接矩阵、图学习层学习到的动态邻接矩阵以及时间卷积得到的节点特征矩阵来整合节点及其邻居信息,提取交通速度数据的动态空间特征。
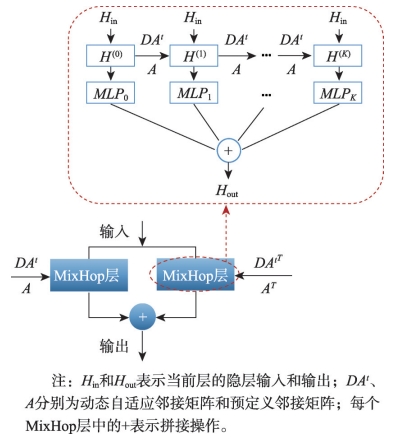
图2 图卷积模块结构
2.3 时间卷积模块
为了帮助模型更好地理解历史交通速度对未来的影响,构建时间卷积模块,旨在捕捉交通速度数据随时间变化的动态特征,并识别其时序依赖性。MTDGNN模型设置多个时间卷积模块,控制其感受野大小的超参数扩张因子d以q的指数速率增加,可以提取不同时间尺度的特征,从而有效处理复杂的时序动态信息。
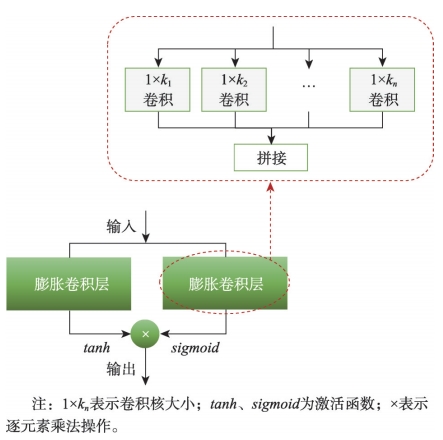
图3 时间卷积模块结构图
3 实验设置
3.1 研究区域与数据说明
实验使用到的数据来源于Q-Traffic Dataset,该数据集涵盖了2017年4月1日至5月31日北京市百度地图用户约1.14亿条道路查询数据,以及相应的交通速度数据和道路网络信息。为了提高交通速度的可预测性,对于每个路段,采用15 min时间窗口的简单移动平均对速度数据进行了平滑处理。
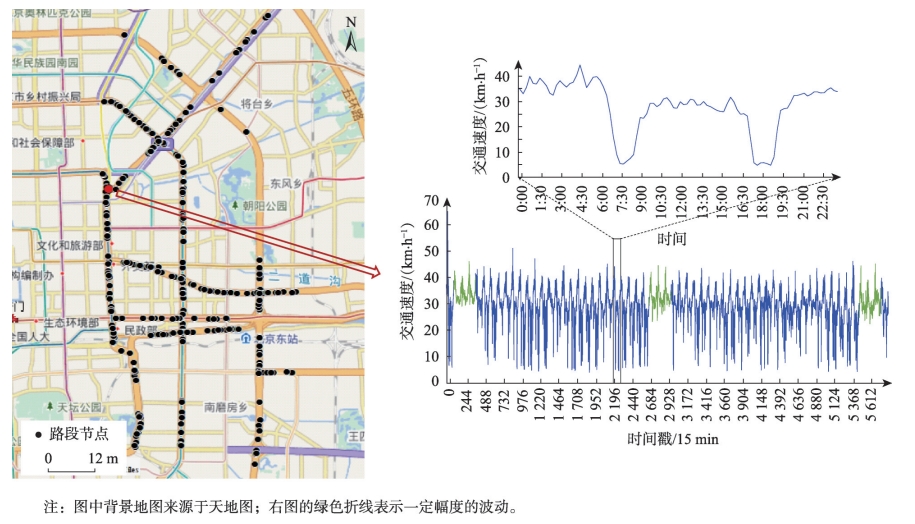
图4 北京市东部城区实验路段节点分布
3.2 评价指标
实验选取了3个不同的指标来对模型精度进行评价,分别为平均绝对误差(MAE)、均方根误差(RMSE)以及平均绝对百分比误差(MAPE)。其中,MAE描述预测偏差的绝对值,RMSE反映预测结果的稳定性,MAPE表示预测值与真实值的相对误差。这3个评价指标的值越小,则模型的预测精度越高。
4 结果与分析
4.1 预测结果分析
选取MTDGNN模型对某日中午12:00交通状况的30 min步长预测结果进行可视化,结果如图7所示。整体来看,北京市东部城区主干道大部分道路的速度处于中低速水平,交通拥堵现象较为普遍,城市交通压力较大。
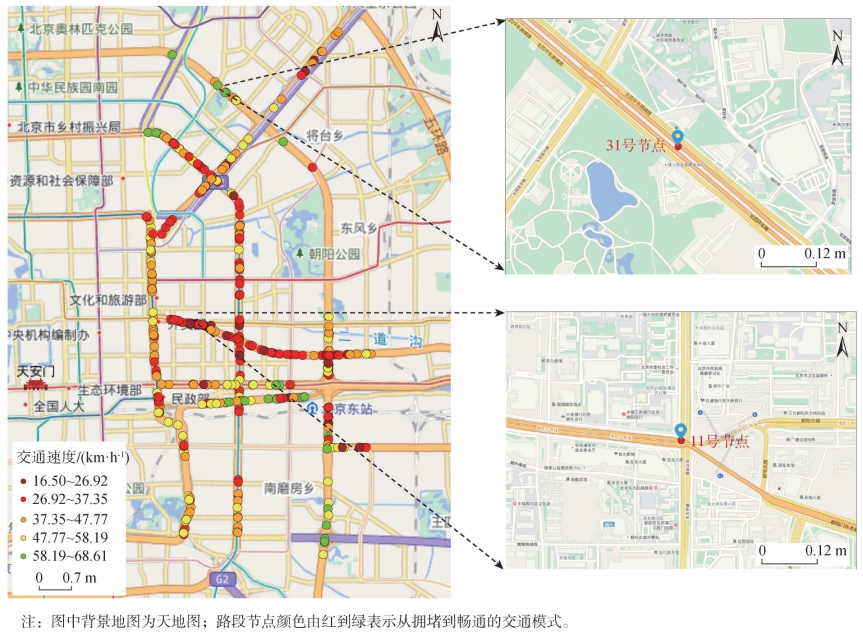
图7 某日12:00预测速度空间分布
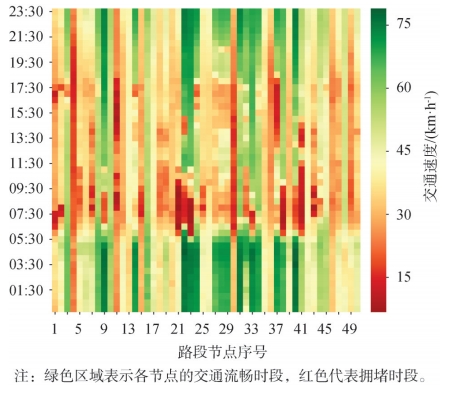
图8 前50个路段节点的预测速度热力图
4.2 预测性能分析
本文选择研究区域内2条路段节点(图10中的路段a和路段b)作为分析对象,以便对实验结果进行直观展示与分析。图11和图12分别展示了这2个路段在整个测试集范围以及特定某一天的30 min步长预测结果与真实值的对比情况。
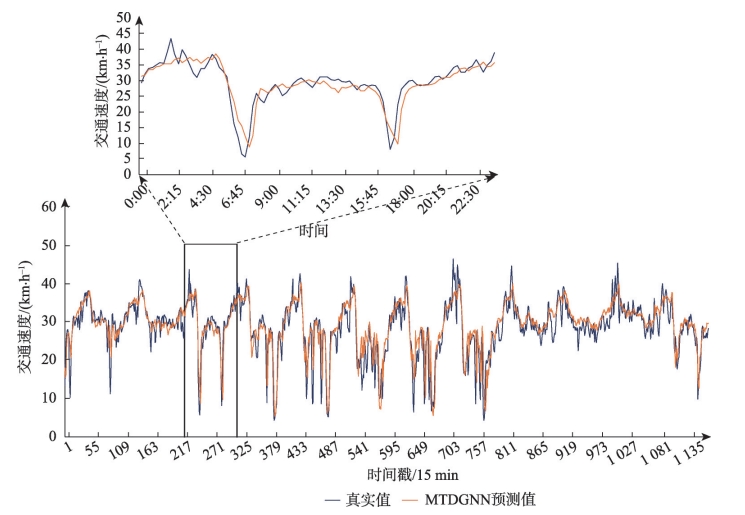
图9 路段a预测值与真实值对比
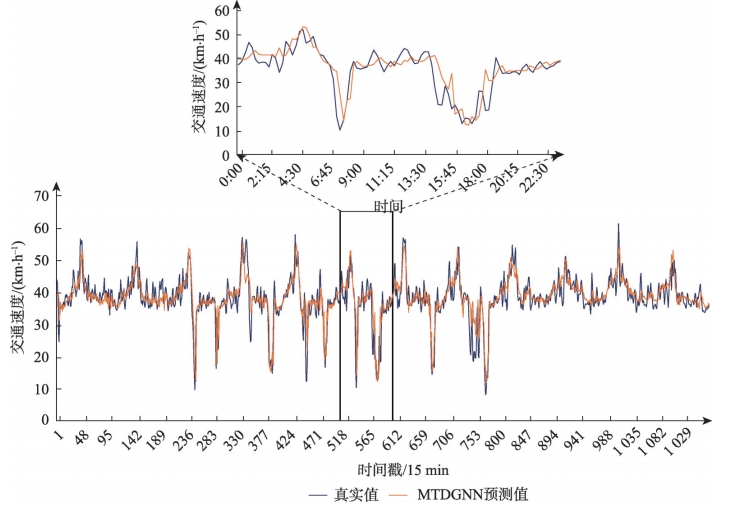
图10 路段b预测值与真实值对比
4.3 模型对比分析
为了进一步验证模型的先进性与有效性,将MTDGNN模型与9种基准模型进行了比较,基于北京市交通数据集进行实验,并采用MAE、RMSE、MAPE比较评估模型的预测效果。
| 方法 | 30 min MAE | 30 min RMSE | 30 min MAPE/% | 120 min MAE | 120 min RMSE | 120 min MAPE/% |
|---|---|---|---|---|---|---|
| HA | 4.52 | 7.48 | 15.06 | 6.66 | 10.67 | 22.83 |
| MTDGNN(本文方法) | 2.39 | 3.89 | 7.92 | 3.10 | 5.34 | 10.74 |
表3 不同模型不同时间步长预测性能比较
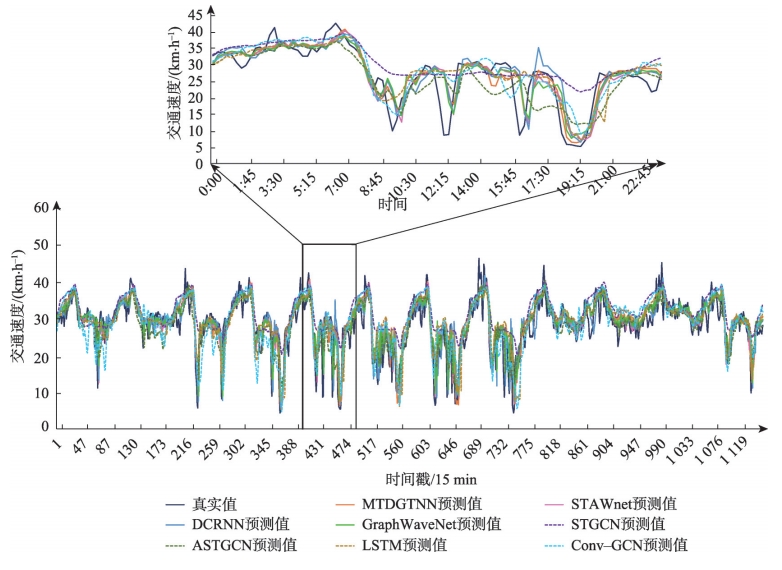
图11 各模型预测结果对比
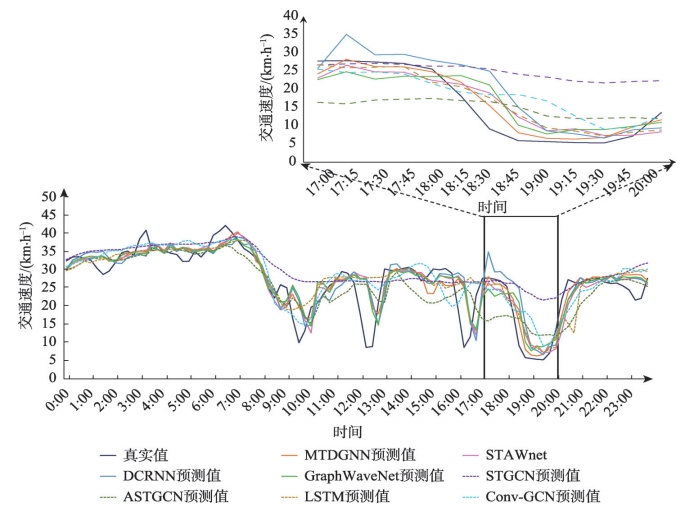
图12 各模型一日预测结果对比
5 结论
在城市交通预测任务中,各路段间的交通速度受到多种因素影响,表现出强烈的动态时空相关性。为此,本文构建了MTDGNN交通速度预测模型,并利用北京市东部城区的真实交通数据进行实验验证。主要研究成果及结论如下:
- 本文提出的MTDGNN模型基于实时交通信息和静态路网拓扑,构建动态自适应图,反映交通网络的实时变化,克服了静态图在建模时变交通图拓扑时的局限性。同时,MTDGNN充分考虑到交通数据的动态特征与静态路网拓扑结构的相互作用,可以更全面理解交通流的波动模式。MTDGNN模型采用混合跳跃传播层和膨胀卷积层,分别作为图卷积模块和时间卷积模块,从不同空间尺度和时间尺度有效捕捉了交通网络的动态时空关联特征。
- 利用北京市东部城区主干道交通数据,通过MTDGNN模型对未来两小时的道路交通速度进行预测,预测结果与真实交通状况相符。其中,15 min的预测精度指标MAE、RMSE、MAPE分别为1.41、2.15、4.51%,120 min的预测精度指标MAE、RMSE、MAPE分别为3.10、5.34、10.74%。
- 通过与9个基准模型和7个消融实验模型进行对比,实验结果显示,MTDGNN模型在MAE、RMSE和MAPE评估指标上均取得了最优的预测精度。与几种基准模型相比,平均MAE、RMSE分别降低了至少2.24%和3.98%,表明该模型在复杂交通场景中的优越性与鲁棒性,验证了MTDGNN模型在交通速度预测中的有效性,尤其是在较长预测步长的情况下,该模型相比其他基线模型表现出更高的准确性。
应用前景
MTDGNN模型可以为交通部门提供科学依据,有助于优化城市交通管理,帮助实现智能交通和可持续发展。鉴于交通速度受实时天气变化、突发事件等多重因素的影响,后续研究将引入更多外部信息,以进一步提升模型的预测性能。