1 引言

交通预测问题是指在给定路网结构和一组历史交通状态数据的情况下预测未来一段时间内的交通状态，例如速度、流量、行程时间等。它是智能交通领域的核心和热点问题之一，准确、可靠的交通状态预测信息是诸多智能交通系统应用的基础。高速公路和城市道路是交通预测问题最主要关注的2个场景，但由于城市道路中存在着连接模式更为复杂的交通网络，相较于高速公路，城市路网中的交通预测仍面临较大的挑战。

交通预测经历了由时间序列预测问题转变为时空序列预测的过程。在早期，交通速度、流量等交通状态数据被视为时间序列数据，因此主要采用时间序列预测模型来进行交通预测。例如，以循环神经网络（RNNs）及其变种（LSTM、GRU）为代表的深度学习模型被广泛用于捕捉交通状态时间依赖的动态变化。然而，同时具有时间和空间的相关性是交通状态数据区别于其他时间序列数据的重要特征，在交通预测问题中进行空间相关性的建模是必要的。

在前期对于空间的建模主要采用卷积神经网络（Convolutional Neural Network, CNN）的方式，即将路网建模为欧氏空间的网格，再将交通变量映射为格网数据。CNN算子不需要考虑全局特征，可以更高效地识别输入数据中的局部模式，同时还具有参数共享的特性，使得模型的参数数量少，计算复杂度低。然而这种方式会损失道路网络原本的拓扑结构，难以充分捕获交通网络中复杂的空间关系，且无法支持导航等下游交通应用。

图卷积神经网络（Graph Convolution Network, GCN）通过引入消息传递机制，将卷积操作扩展到图结构数据，因此可以对非欧结构路网中的空间依赖进行建模。GCN的消息传递过程包括2个关键步骤：① 邻域聚合，即通过图的邻接关系，将节点的特征从其邻居节点聚合到中心节点；② 特征变换，即对聚合后的特征进行线性变换以提取高维信息。这种机制使GCN能够利用路网的拓扑结构建模路段间的空间关系。在交通预测问题中，GCN凭借其对复杂网络结构的优秀建模能力，逐步成为时空序列建模的重要工具，并被广泛应用于交通速度、流量和行程时间等预测任务中。

2 转向图卷积神经网络

2.1 问题定义

交通路网通常被建模为有向图G=(V, E)。节点集V中的每一个节点i∈V表示一个路段。当节点i和j相邻且从起点i可以到达终点j时存在边eij∈E，表示车辆从路段i行驶至路段j的路径。|V|和|E|分别为节点的数目和边的数目。节点之间的邻接关系可以表示为邻接矩阵，记为：A∈R|V|×|V|。

以交通速度预测为例，t时刻在节点i∈V观测到的交通速度可记为xti。对于整个路网G，t时刻的交通速度可以表示为向量Xt={xt1, ..., xti, ..., Xt|V|}T。给定整个路网上m个时刻的历史交通速度序列{Xt-m+1, Xt-m+2, ..., Xt}以及路网的拓扑结构信息G，交通预测的目的是预测接下来n个时刻的未来交通速度{Yt+1, Yt+2, Yt+n}，其可以形式化为：

{Yt+1, Yt+22, ..., Yt+n} = F({Xt-m+1, Xt-m+2, ..., Xt}; G)

式中：F(·)是一个基于历史信息待求的映射函数。

2.2 TurnGCN定义

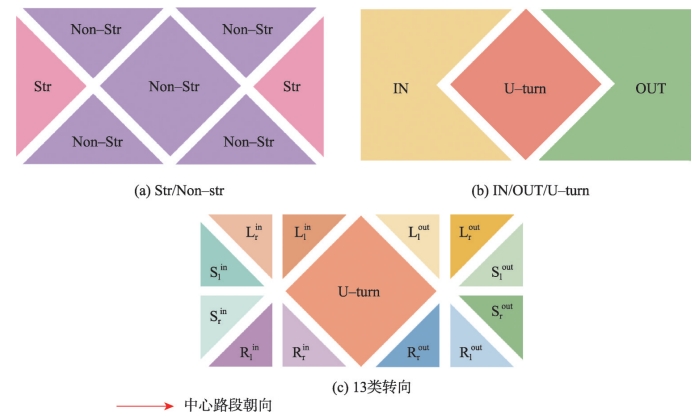
将交通网络抽象为图结构的数据是非常自然的，但是路段具有行驶方向、转向规则以及交通限制等特性，这将交通网络区别于传统的图结构数据，例如社交网络，引文网络等。本研究将路段间的转向关系归纳为几种固定的模式：将中心路段的邻接路段分为上游路段、下游路段和掉头路段。

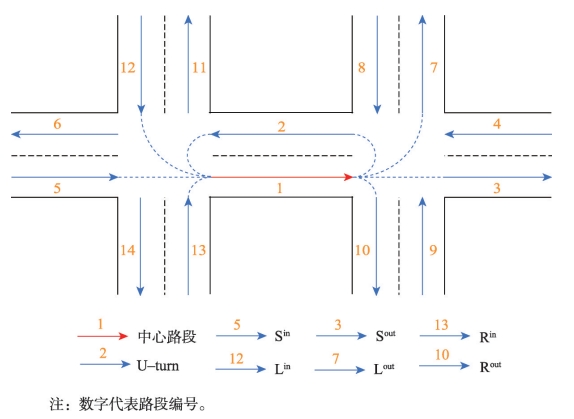
邻接路段转向关系模式分类

图1 邻接路段转向关系模式分类

依据上文归纳的路段间转向关系模式，交通路网可进一步被建模为有向异构图GH=(V, E, TE)，其中节点集V中的每一个节点i∈V表示一个路段,边集E包含不同节点间各种类型的转向关系，TE:E→ε是边类型的映射函数，将每条边eij映射到边类型集合ε中的一个元素，ε={Sin, Lin, Rin, Sout, Lout, Rout, U-turn}。

由于边集E中的边对应着不同类型的转向关系模式，对于异构图GH，传统的GCN并不能直接对其进行卷积运算。

TurnGCN是针对建模了转向关系的GH进行卷积运算的与GCN不同的新型图卷积网络。以图3中Link 5和Link 7的计算为例，依据上文中的定义首先可以得到2条中心路段7种转向模式分别对应的邻接路段，转向关系模式数量的固定使得对不同中心路段使用同一套参数进行转向特征的聚合成为可能，这使得TurnGCN具有参数共享的特性。

2.3 TurnGCN实现

TurnGCN在对节点的空间关系进行建模时考虑了中心路段与其邻居路段的转向关系和相对位置。它在计算过程中使用转向表来替代传统GCN使用的邻接矩阵，将节点特征映射为欧氏空间的特征栅格，再使用CNN卷积操作实现邻域特征的聚合。

2.3.1 转向表构建

以一阶TurnGCN为例，本研究依据图1中中心路段与邻接路段转向关系的7种固定模式构建转向表。根据路网的拓扑结构，构造出转向表T∈R|V|×turn，其中表中的元素Ti,tr表示与节点i存在第tr种转向关系的节点id，Ti,tr也可以为空或多个节点id的集合。

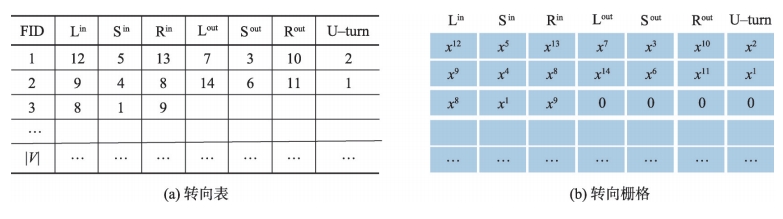
转向表与转向栅格示例
图2 转向表与转向栅格示例

2.3.2 TurnGCN计算过程

TurnGCN的计算过程主要分为2步，如图6所示。第（1）步是依据转向表将t时刻原始的交通变量Xt∈R|V|×F映射为转向栅格，即XGrid∈R|V|×turn×F，其中F为特征的维数，turn为邻接路段间转向关系的类别数。第（2）步为特征的聚合，即使用CNN卷积核卷积的方式进行邻接节点转向特征的聚合，单个卷积核的形状为turn×1，其沿着节点堆叠的方向平移，即XGrid的第一维度。

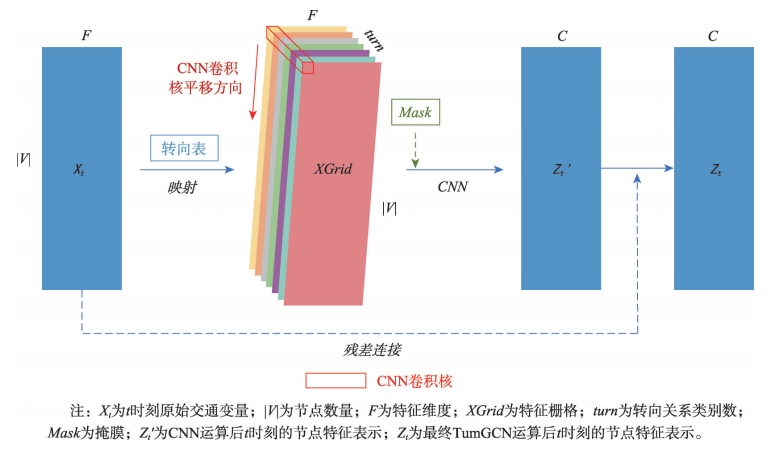
TurnGCN计算过程详细示意图
图3 TurnGCN计算过程详细示意图

2.3.3 复杂度分析

当图的节点数为N，特征维度为F，卷积网络的层数为L时，各图卷积方法复杂度对比如表1所示。

表1 图卷积方法复杂度对比
模型 空间复杂度 时间复杂度
GCN O(N2+LFN+LF2) O(L(FN2+F2N))
GCN+attention O(N2+LN2+LFN+2LF2) O(L(2FN2+2F2N))
TurnGCN O(turn*N2+LFN+turn*LF2) O(L(turn*FN+turn*F2N))

3 实验配置

3.1 数据集

本文选取了SeoulUrban和SHSpeed 2个现实世界城市道路的交通速度数据集作为实验数据，来验证TurnGCN性能的优越性。2个数据集中均包含了路段的连通情况，端点的经纬度信息等，可用于进行转向表的构建。

3.2 基准模型设置

本文将4种用于交通预测的经典时空图卷积基线模型中的图卷积层，或加入空间注意力机制的图卷积层替换为一阶TurnGCN，以验证所提出的TurnGCN卷积网络的效果。

  1. 时序图卷积（T-GCN）。T-GCN结合了GCN和GRU来建模交通变量的时空相关性。
  2. 残差图卷积长短期记忆神经网络（RGC-LSTM）。RGC-LSTM结合GCN和LSTM来建模交通变量的时空依赖。
  3. 时空图卷积神经网络（ST-GCN）。ST-GCN结合ChebNet和GLU来建模交通变量的时空相关性。
  4. 混合注意力时空图卷积（ASTGCN）。建模交通流的3种时间属性，即近期、日周期和周周期依赖关系。

3.3 环境与模型配置

本研究使用历史1 h内的速度变化序列来预测未来1 h内的速度，即实验中数据集Urban-150历史及未来滑动窗口设置为12，数据集SHSpeed历史及未来滑动窗口设置为6。当同一转向关系包含多条邻接路段时，使用其中随机选取的路段特征值来表示该转向模式的特征。为便于模型训练和精度评价，将数据集分为训练集（60%）、验证集（20%）、测试集（20%）。

3.4 评价指标

3种常用的指标用于评估模型的预测精度，分别是均方根误差（Root Mean Square Error, RMSE）, 平均绝对误差（Mean Absolute Error, MAE），以及平均绝对百分比误差（Mean Absolute Percentage Error, MAPE）。3种指标的值越小代表模型预测的误差越小，即模型的精度越高。

4 结果及分析

4.1 实验结果

如表4所示，相比于使用GCN来对空间依赖进行建模的模型，将GCN的部分替换为TurnGCN后模型的预测精度均有了显著的提升，且在短时间预测和长时间预测中均表现出优秀的性能。和加入空间注意力机制的GCN相比TurnGCN也有着更好的表现，同时所需的参数量显著减小。

表4 1 h的交通预测精度对比（*表示使用TurnGCN）
模型 30 min RMSE 30 min MAE 30 min MAPE(%) 60 min RMSE 60 min MAE 60 min MAPE(%)
T-GCN 3.38 2.56 11.94 3.69 2.80 13.13
T-GCN* 3.13 2.32 10.51 3.47 2.61 12.05

4.2 转向关系的空间依赖捕捉

在交通网络中，与中心路段具有不同转向关系的邻接路段，可能对中心路段的交通状态有着不同程度的影响。TurnGCN可以在训练过程中自适应地学习并捕捉这种空间依赖的异质性，并通过权重参数的数值大小体现。

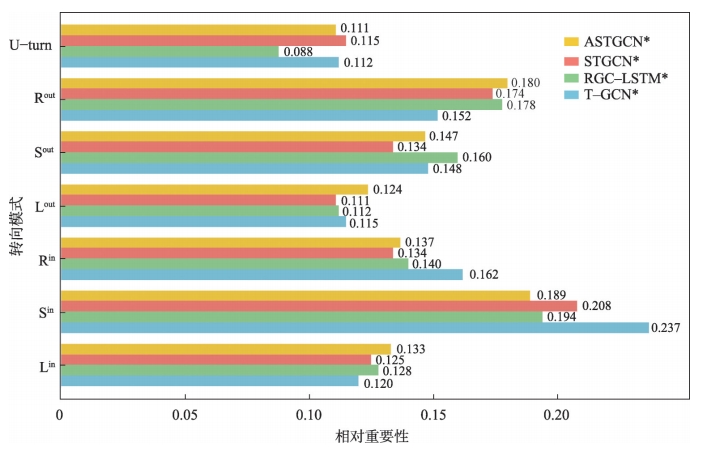
不同转向模式的相对重要性
图4 不同转向模式的相对重要性

4.3 敏感度分析

卷积算子阶数的增加和多层叠置可以使得网络有更大的空间感受野，以此捕获更大范围的空间依赖关系。多头的运算则使模型可以从多个角度学习数据中的特征，进而捕获到不同类型的空间依赖。

不同转向关系分类方式
图5 不同转向关系分类方式

5 总结与展望

本研究提出了一种全新的图卷积神经网络TurnGCN，旨在通过显式建模城市道路网络中路段间的转向关系来提升交通预测性能。具体而言，TurnGCN将城市路网建模为异构图，其中边表示路段之间的转向关系。在前向传播过程中，TurnGCN通过引入转向表，将邻居路段的特征映射为欧几里得空间中的转向特征栅格，并利用CNN卷积神经网络对邻居特征进行聚合，从而实现异构图的卷积运算。

实验表明，相比传统的GCN，基于TurnGCN的模型在多个评估指标上均取得了更高的预测精度，由此说明TurnGCN能更充分地建模交通路网中的空间相关性。同时，相比于考虑全局来建模空间关系异质性的使用空间Attention的GCN，TurnGCN空间局部性和参数共享的特性使得它在参数量不大的情况下依旧能取得优秀的性能。

TurnGCN具有归纳学习的特点，不使用邻接矩阵来进行图卷积使得它在训练过程中无需知道整个路网的拓扑结构，这让它可以对路段进行小批次的训练。在未来的实验中，可以验证TurnGCN被用在更大规模路网中的可能性，还可以结合分布式图计算框架实现大规模数据的并行处理，以实现城市级的交通预测应用。