基于通勤流分析的城市多中心空间结构评估与优化方法

1 引言

多中心空间战略在解决城市通勤时间过长、交通拥堵、空气污染、环境恶化等问题方面发挥了积极作用，被广泛应用于国内外的城市规划实践中。城市通过建设多中心空间格局，使就业岗位和公共服务等资源的分布适度分散化，为就业人口提供负担得起的、尽可能接近工作地点的居住地点，从而促进城市空间资源的优化配置，提高城市的运行效率，缓解许多的"城市病"。

2020年4月，习近平总书记在中央财经委员会第七次会议上提出，"要建设一批产城融合、职住平衡、生态宜居、交通便利的郊区新城，推动多中心、郊区化发展......逐步解决中心城区人口和功能过密问题"。可见，在我国的城市建设中推行多中心空间战略，是坚持"以人民为中心"的城市发展思想的具体体现，有助于进一步推动人居环境建设，实现高质量发展，其意义重大。

为了最大化多中心空间战略的价值，为调整和优化城市空间发展政策提供依据，对城市空间战略的实施效果进行评估具有重要的基础支撑意义。

研究现状

已有研究主要依靠问卷调查数据、产业经济数据、土地调查数据等
评估方法多采取定量分析和定性分析相结合的方式
缺乏明确、可量化的评估目标和比较标准

研究创新

提出整合多种机器学习模型的技术框架
以城市平均通勤距离最小化为判别标准
构造评估指标量化评价城市空间结构

2 研究设计

2.1 城市多中心结构对通勤流分布的影响机制

本研究建立城市空间结构与城市通勤格局之间的关联，将其作为识别城市最优空间结构的技术基础。该关联包含了城市就业中心的空间分布、就业人口的工作地（简称"工作地"）、就业人口的居住地（简称"居住地"）、城市通勤流分布这4个要素，其作用机制可简要概括为一个三阶段过程。

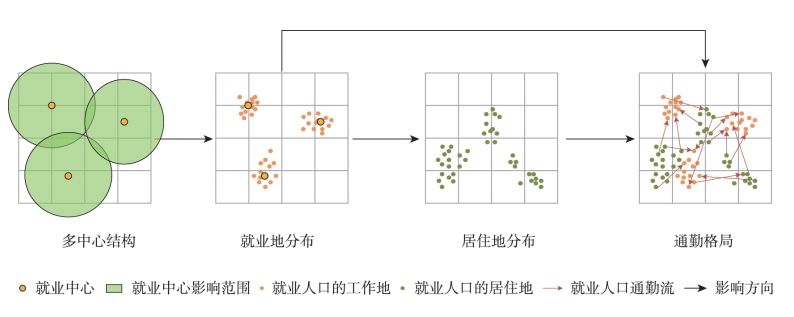
图1 城市多中心结构对通勤流分布的影响机制

阶段一

城市多中心格局刻画就业岗位的分布情况。城市中就业岗位的分布往往围绕若干中心，呈现有规律的距离衰减特征，本研究通过高斯混合模型（Gaussian Mixture Model, GMM）对这一映射关系进行描述和刻画。

阶段二

工作地分布影响居住地分布。根据"共同定位假说"（Co-location Hypothesis），在经济允许的情况下，就业人口在选择居住地时通常尽可能接近其工作地，以最大限度地缩减交通成本。本研究使用XGBoost模型反映上述机理。

阶段三

就业人口在居住地和工作地之间形成规律的通勤行为，构成城市的通勤格局。

2.2 实证技术路线

本研究的技术路线包括4个阶段：①数据准备阶段；②模型训练阶段；③格局优化阶段；④决策支持阶段。

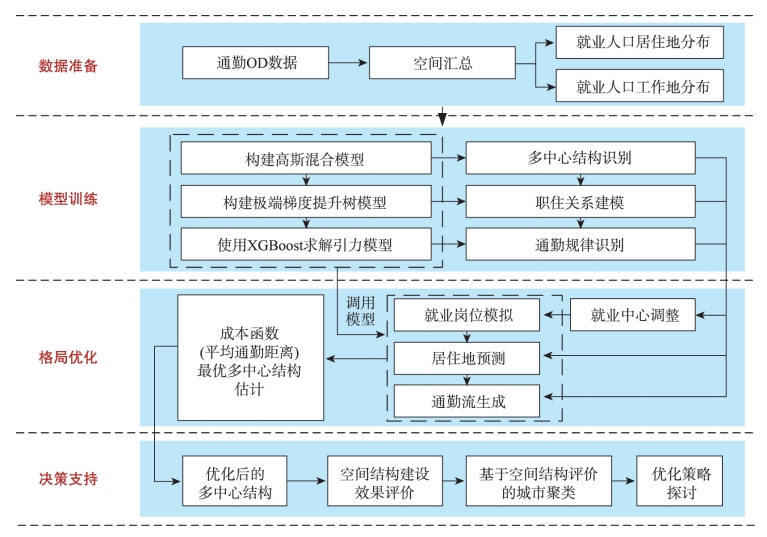
图2 研究技术路线

2.3 最优多中心结构估计

2.3.1 基于高斯混合模型的多中心结构识别和就业岗位模拟

假定一个城市中有K个就业中心，则对于地点x来说，其就业岗位数量n(x)由式（1）、式（2）给出。

n(x)=n∑_k=1^Kπ_kN(x|μ_k,Σ_k)

N(x|μ_k,Σ_k)=1/(2π|Σ_k|^1/2)exp(-1/2(x-μ_k)^TΣ_k^-1(x-μ_k))

式中：N表示城市工作人口总量；π_k为权重，表示混合模型中每个就业中心的影响力；N(x|μ_k,Σ_k)是二维高斯密度函数，表示每个就业中心周边就业岗位的分布特征；μ_k是第k个中心点的地理坐标；∑_k是二维协方差矩阵，代表就业中心影响力的衰减速度。

2.3.2 基于极端梯度提升树的职住关系建模

本研究使用极端梯度提升树算法（eXtreme Gradient Boosting, XGBoost）描述工作地分布对居住地分布的影响。假设模型共有N棵决策树，其计算过程如式（3）-式（5）所示：

ẏ_i^(N) = ∑_i=1^N f_j(x_i), f_j∈F

Obj_t = ∑_i=1^N(y_i,ẏ_i^(t)) + ∑_i=1^tΩ(f_t)

Ω(f_t) = γT + 1/2λ∑_j=1^Tω_j²

2.3.3 基于引力模型的通勤规律识别

引力模型是常用的空间相互作用模型之一，被广泛用于各种地理现象的研究。本文构建的引力模型描述为式（7）。

ln(T_ij) = κ + λ₁ln(Pop_i) + λ₂ln(Pop_j) + βln(Dist_ij) + ε_ij

2.3.4 基于智能优化算法的最优多中心结构估计

对城市而言，最优多中心结构是使平均通勤距离最小的中心权重分配。本研究使用自适应差分进化算法（Self-adaptive Differential Evolution, SADE）来完成优化任务。

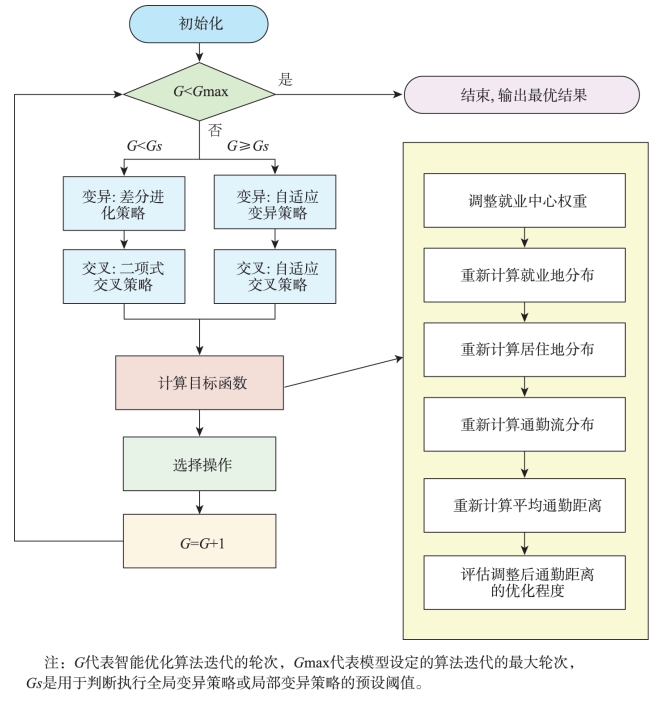
图3 基于SADE算法的最优多中心结构估计过程

2.4 多中心空间结构的建设效果评估

本研究提出可优化度OPT_global和均衡化趋势OPT_balance两项评估指标。

可优化度 (OPT_global)

衡量城市现状多中心结构与最优多中心结构之间的差距，体现空间政策理论上的最大实施成本。

OPT_global = 1/N ∑_i=1^N |w_i'-w_isub>|

均衡化趋势 (OPT_balance)

衡量从现状多中心结构演变到最优多中心结构后，各城市中心的权重值方差的变化趋势。

OPT_balance = v' - v

3 实证研究

3.1 研究区概况与研究数据

3.1.1 研究区概况

本研究的范围为京津冀大都市区中各直辖市、地级市的城区，具体包括北京市和天津市的全部行政辖区范围，以及河北省各地级市的市辖区，总面积53,263.9 km²。

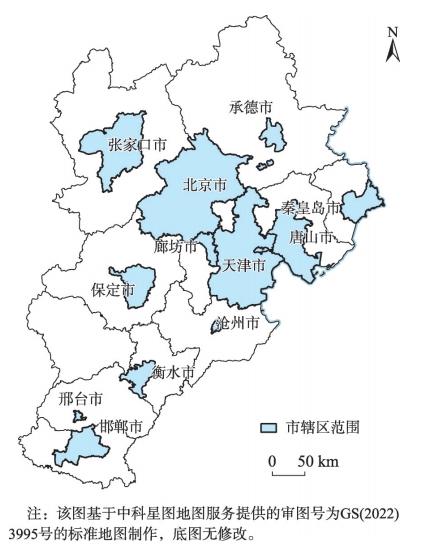
图4 京津冀大都市区范围

3.1.2 实验数据

本研究主要使用百度地图慧眼提供的2018年9月、2022年9月2期通勤OD数据，该数据以2 km网格为基本单元，记录了每一对网格之间的通勤流规模。

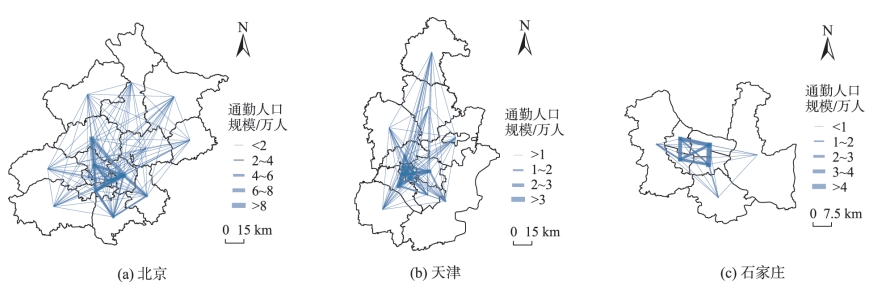
图5 代表性城市市辖区的现状通勤流分布情况

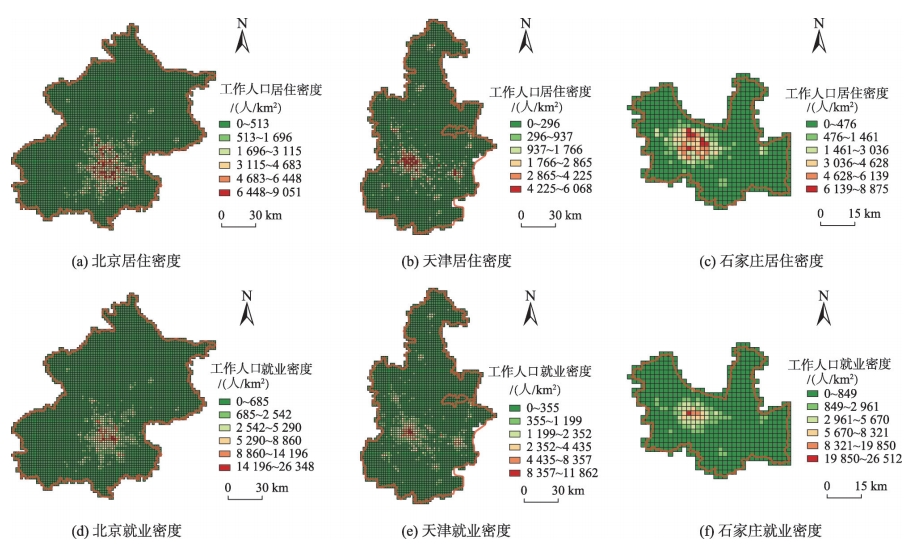
图6 代表性城市市辖区的工作地和居住地分布现状

3.2 模型表现

实证研究中各模型的性能如表1所示。一方面，模型的单步误差均比较小，表明本研究所使用模型能较好的刻画就业人口的职住特征。另一方面，各模型的累积误差虽略高于单步误差，但差距并不悬殊，表明整体技术框架较为可靠，误差的传递基本可控。

表1 模型精度评价

城市	工作地分布估计累积误差	居住地分布估计累积误差	通勤流分布估计累积误差
北京	MAE: 292.88, MSLE: 3.92	MAE: 183.27, MSLE: 3.60	MAE: 2.21, MSLE: 1.25
天津	MAE: 223.39, MSLE: 5.56	MAE: 166.40, MSLE: 3.67	MAE: 2.18, MSLE: 1.27

3.3 现状与最优多中心结构识别

3.3.1 现状多中心结构识别

基于前述的方法，本研究对京津冀大都市区内13个城市的空间结构进行识别，发现各城市的市辖区均呈现明确的多中心结构，且绝大部分城市中各中心的发展水平不均衡。

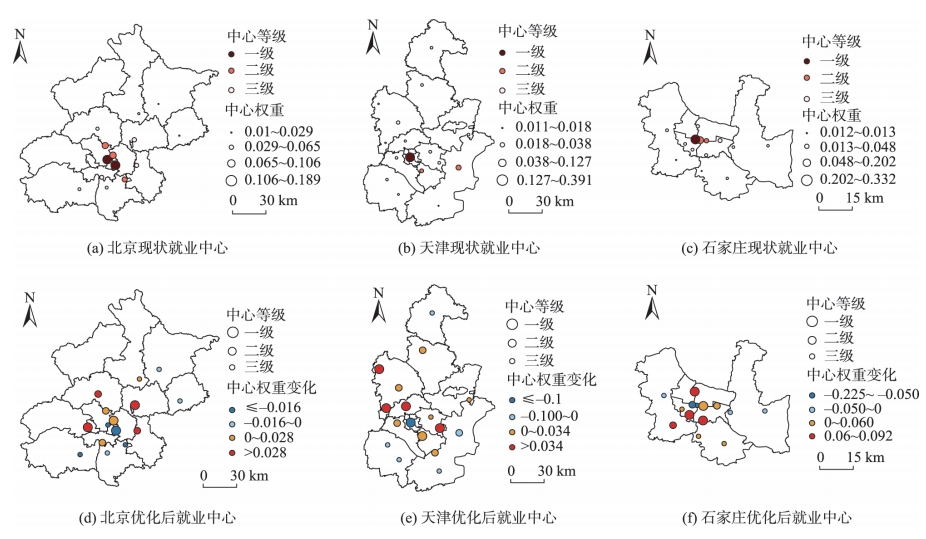
图7 代表性城市市辖区的就业中心识别与优化结果

3.3.2 最优多中心结构估计

与现状相比，空间结构优化后各城市的通勤效率有了显著的改善。大都市区的北部地区平均通勤距离缩减幅度相对较大，反映该地区存在较高的空间结构优化收益。

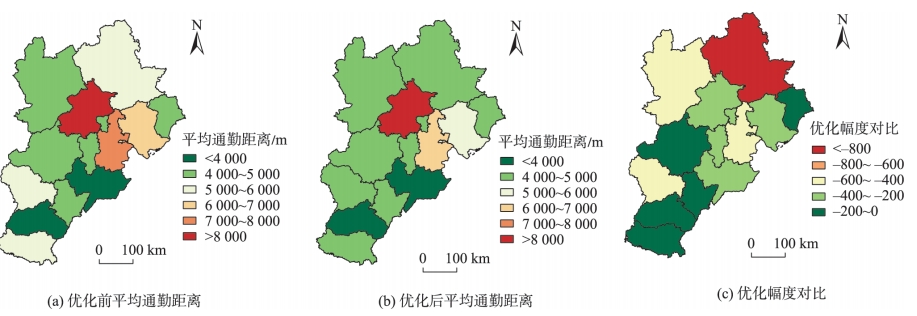
图8 各城市市辖区空间结构优化前后的平均通勤距离变化对比

3.4 空间结构的建设效果评价和优化策略探讨

研究范围内各城市的可优化度和均衡化趋势两项评价指标的计算结果如图10所示。

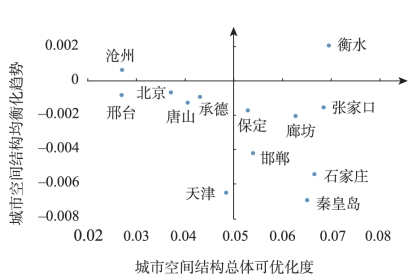
图10 各城市空间结构的建设效果评估

微调极化型

主要指沧州市。此类城市现状各中心的权重接近最优值，调整方向为增加高等级中心的权重，促进空间结构进一步极化。

大幅极化型

主要指衡水市。此类城市的空间结构仍有较大的调整余地，调整方向同样是强化高等级中心的影响力。

微调均衡型

主要包括邢台市、北京市、唐山市、承德市、天津市5个城市。此类城市的多中心发展战略落实较好，下一步的优化策略是弱化高等级中心的影响、积极培育外围的低等级中心。

大幅均衡型

主要包括保定市、廊坊市、张家口市、邯郸市、石家庄市、秦皇岛市6个城市。此类城市需加大空间结构优化的力度，促进高等级中心的疏解，提高空间格局的均衡度。

4 结论与展望

对城市多中心结构进行较为客观、量化的评价和优化，是城市治理领域的一个重要问题。针对此问题，本研究基于时空大数据技术和机器学习模型提出一个技术框架。该框架根据城市就业中心分布对通勤格局的复杂影响过程，在不同环节中引入不同的模型，统筹实现了城市空间结构的现状评价和优化模拟等功能。

贡献一

提出了一种最优多中心格局的识别方法，确立了空间结构评估的比较对象，为实现精准的空间发展引导提供了技术支撑。

贡献二

提出了一种城市多中心空间结构建设效果的评估方法，从2个维度考核城市现状多中心结构的完善程度。

贡献三

在京津冀大都市区中实践了上述方法，其分析结果对该地区未来的精细化治理具有参考价值。

研究展望

考虑就业中心数量增减的情况
从更加综合的视角来深化研究
完善评估指标以体现中心之间的空间关系