引言

空间关系是指地理实体之间所具有的空间特性关系，它反映着人类对空间形态的推理与描述，是人类认知空间形态的途径。空间关系理论作为空间信息科学的理论基础与核心内容，广泛应用于空间数据的组织、查询、分析、推理、数据挖掘、制图综合质量评价与控制，以及多源、多类型、多尺度空间数据的集成与更新等领域。

空间关系包括拓扑关系、方向关系、距离关系、相关关系和相似关系，目前国内外在前4种空间关系的研究已取得颇为丰富的成果，然而，对于空间相似关系的研究仍显不足。

空间相似关系用于描述和表达地理空间及其转换生成的地图空间目标之间的关系。空间相似关系的强弱可由相似度衡量，Yan于2010年提出基于集合论的多尺度地图空间相似关系定义，认为对象间的相似性可通过多个特征指标进行评估，这些特征指标的相似度之和即为对象间的相似度。

"目前，基于统一理论对各相似性特征指标形式化描述模型的建立，以及在此基础上的整体相似度计算模型方面的研究仍显不足。大多数研究仅提供了目标群组在多尺度地图空间的相似度计算模型，对于各空间相似性特征指标在空间相似度计算模型中的特征指标及其权重的选取，普遍依赖于问卷调查、专家评分或自定义权重，客观性和通用性难以得到保障。"

本文以点群目标为例，系统梳理、统计与分析了点群空间相似度计算模型中常用的特征指标，并选取其中最为关键的属性相似度、分布范围相似度、分布密度相似度、距离相似度、方向相似度及拓扑相似度作为研究对象，采用多种权重确定方法对这些特征指标进行权值计算与排序，旨在提供一组客观、统一的权重值，为点群目标空间相似度计算模型提供可靠的理论基础。

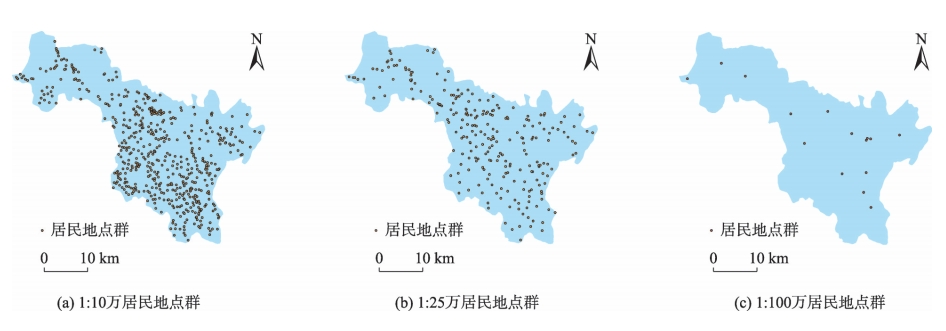
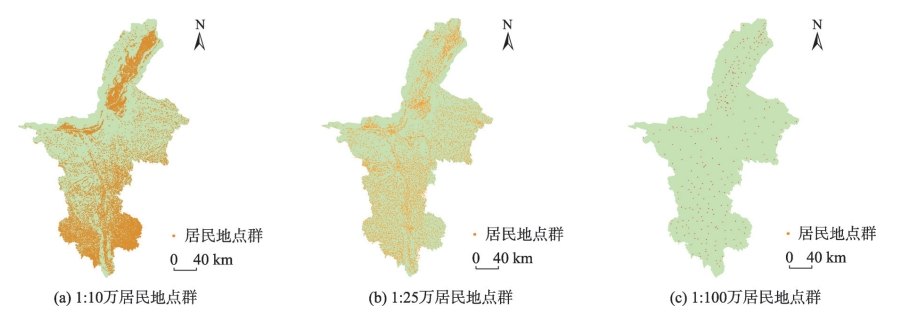
影响点群要素空间相似度计算的特征指标

研究表明，点群的空间相似度计算模型通常考虑到的特征指标包括：属性相似度、分布范围相似度、分布密度相似度、距离相似度、方向相似度、拓扑相似度、统计相似度、中心相似度、轴线相似度。根据出现次数的排名，本研究选取前6项指标作为研究对象。

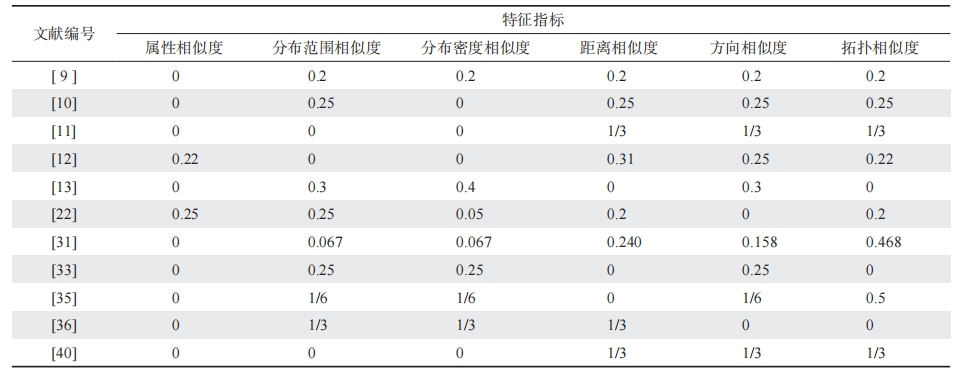
部分文献采用的空间相似度计算模型特征指标权值

图1 部分文献采用的空间相似度计算模型特征指标权值

属性相似度

通过点群的平均重要程度计算：

sim属性 = min(Ī1, Ī2) / max(Ī1, Ī2)

其中Ī1、Ī2分别表示尺度变化前后的点群平均重要程度。

分布范围相似度

点群分布范围相似度定义为：

sim分布范围 = 1 - |s1 - s2| / max(s1, s2)

其中s1、s2分别表示尺度变化前后的凸壳面积。

分布密度相似度

点群密度相似度定义为：

sim分布密度 = 1 - |n1/s1 - n2/s2| / max(n1/s1, n2/s2)

其中n1、n2分别表示尺度变化前后地图上的点群数量。

距离相似度

点群的距离相似度定义为：

sim距离 = 1 - |b1/a1 - b2/a2| / max(b1/a1, b2/a2)

其中a1、a2表示标准差椭圆短轴长度；b1、b2表示标准差椭圆长轴长度。

方向相似度

点群的方向相似度定义为：

sim方向 = cos(θ1 - θ2)

其中θ1、θ2分别表示标准差椭圆与x轴之间的夹角。

拓扑相似度

点群拓扑相似度定义为：

sim拓扑 = 1 - |D1 - kD2| / max(D1, D2)

其中D1、D2分别表示拓扑邻居数；k=√(m1/m2)，m1、m2为地图比例尺。

点群整体相似度

作为一个整体，点群的相似性不应仅从单一方面进行考虑，而应综合以上6项相似性特征指标。即，点群整体相似度是各特征指标加权相似度值的线性和：

SIM = Σ(ωi · simi)

其中ωi表示各特征指标所占的权重；simi表示各特征指标的相似度值。

权重确定方法

目前，权重确定方法主要可分为3类：主观赋权法、客观赋权法以及主客观综合赋权法。本研究采用以下四种方法进行对比分析：

层次分析法(AHP)

类型：主观赋权法

AHP是一种结合定性和定量分析的决策分析方法，旨在解决多目标复杂问题。该方法具有系统性、灵活性、简洁性等优点。

其基本原理是将与决策有关的因素分解为目标层、准则层、方案层，随后通过两两比较打分构建判断矩阵，并计算判断矩阵特征向量以获得各指标的权重。

粗糙集理论(RS)

类型：客观赋权法

RS是一种研究不完整和不确定知识及数据的表达、学习和归纳的理论方法。

其主要优点在于无需提供与问题相关的先验知识，仅依赖于客观数据本身进行分类处理，删除冗余信息，分析知识粗糙度以及属性间重要性与依赖性，从而有效避免主观赋权法中人为因素的影响，使评估结果更加客观。

模糊综合评价法(FCEM)

类型：主客观综合赋权法

FCEM基于模糊数学原理，利用隶属度的概念将定性评价转化为定量评价，能够系统性地解决模糊且难以量化的各种不确定性问题。

FCEM主要的计算步骤包括：确定评价因素集、确定评价等级集、确定模糊关系矩阵、确定评价指标体系的模糊权向量并利用适当的算子将评价矩阵与关系矩阵合成，以获得各被评价对象的模糊综合评价结果向量。

AHP-RS组合权重法

类型：主客观综合赋权法

AHP-RS组合权重法旨在兼顾决策者主观偏好，同时充分利用客观赋权法所包含信息，以有效减少单一权重确定方法可能导致的偏差，从而提升权重分配的合理性与准确性。

该方法通过拉格朗日优化决策模型将AHP与RS结合，其数学表达为：Wi = φωAi + (1-φ)ωRi，其中φ为经验因子，代表决策者对主观经验与客观数据的偏好程度。

实验分析

实验数据

本研究选取了不同地理场景、不同比例尺下的2组点群数据进行实验，兼顾了点群数量和空间分布特征的多样性：

兰州市城区

  • 1:10万比例尺下的533个点
  • 1:25万比例尺下的245个点
  • 1:100万比例尺下的15个点
兰州市城区不同尺度下的居民地点群

兰州市城区不同尺度下的居民地点群

宁夏回族自治区

  • 1:10万比例尺下的17,045个点
  • 1:25万比例尺下的6,525个点
  • 1:100万比例尺下的276个点
宁夏回族自治区不同尺度下的居民地点群

宁夏回族自治区不同尺度下的居民地点群

特征指标 AHP RS FCEM AHP-RS
拓扑相似度 0.42 0.22 0.42 0.36
距离相似度 0.19 0.18 0.17 0.15
方向相似度 0.19 0.14 0.17 0.15
分布范围相似度 0.08 0.14 0.09 0.12
分布密度相似度 0.08 0.14 0.09 0.12
属性相似度 0.04 0.18 0.06 0.10

对比分析结果

  1. AHP与RS对比：AHP确定的6个特征指标权值之间的差距在4种方法中最大，拓扑相似度的权值高达0.42，而属性相似度的权值仅为0.04。RS确定的6个特征指标权值之间的差距则最小，其中权值最高的拓扑相似度与权值最低的方向相似度、分布密度相似度及分布范围相似度之间的差异仅为0.08。
  2. AHP与FCEM对比：AHP与FCEM所获得的权值差异较小，其中拓扑相似度权值完全一致，分布密度相似度和分布范围相似度之间的权值差异仅为0.01，距离相似度、属性相似度以及方向相似度之间的权值差异为0.02。此外，二者的权重排序完全一致。
  3. AHP-RS组合权重法：AHP-RS组合权重法所获得的权值排序与AHP及FCEM的权重排序完全一致，符合实际情况。该方法确定的6个特征指标权值间的差距为0.26，相较于AHP和FCEM所确定的权值间差距0.38和0.36，显示出显著改善。

点群空间相似度计算结果

将AHP-RS组合权值法确定的权重ω拓扑, ω距离, ω属性, ω方向, ω分布范围, ω分布密度=(0.36, 0.15, 0.10, 0.15, 0.12, 0.12)代入点群整体相似度公式，得到不同尺度下点群空间相似度：

研究区 兰州市城区 宁夏回族自治区
1:10万~1:25万 78.77% 78.82%
1:10万~1:100万 36.94% 42.29%
1:25万~1:100万 44.63% 43.39%

根据上表所示点群空间相似度，可以观察到：

  • 当比例尺由1:10万变更至1:25万时，点群目标间的相似度78.77%（78.82%）显著高于比例尺从1:10万变更至1:100万时的相似度36.94%（42.29%）；
  • 同样，比例尺由1:25万变更至到1:100万时，点群目标间的相似度44.63%（43.39%）亦明显高于比例尺从1:10万变更至1:100万时的相似度36.94%（42.29%）；
  • 即，随着比例尺跨度的增大，点群目标间相似度逐渐降低；而随着比例尺的逐渐缩小，地图相似度也呈现出单调递减的趋势。

这与人类在不同尺度下对点群相似度的认知相契合，某种程度上也反映了AHP-RS组合权值法所确定权重的合理性与有效性。

结论

本文基于AHP、RS、FCEM及AHP-RS组合权值法，分别计算了空间点群目标相似度计算模型中多个特征指标的权值及权重排序，包括属性相似度、分布范围相似度、分布密度相似度、距离相似度、方向相似度及拓扑相似度。通过对比分析，发现：

  1. AHP确定的各特征指标权值之间存在较大差异，其中属性相似度的权值极小，削弱了其在空间相似度计算模型中的影响力，导致评价结果失真；
  2. RS由于太过依赖客观数据，导致权重排序相较AHP发生变化，属性相似度排名与实际情况明显不符；
  3. 尽管FCEM在一定程度上改善了AHP所确定的特征指标权值差异较大的问题，但改善效果并不显著，仅将权值差距从0.38减小至0.36；
  4. AHP-RS组合权值法兼顾了主客观因素，显著缩小了权值间的差异，使得评价更接近真实情况。

本文最终提供了一组特征指标权重分配方案：

ω拓扑, ω距离, ω属性, ω方向, ω分布范围, ω分布密度 = (0.36, 0.15, 0.10, 0.15, 0.12, 0.12)

该权重分配方案为点群目标空间相似度计算模型提供了客观且统一的权重值，这在很大程度上解决了以往在计算群组目标（点群）间的空间相似关系时，各特征指标权重选取时存有明显主观偏向且常常依赖被试调查问卷获取的问题，为空间相似关系计算与地图综合提供了可靠的特征指标权重依据。

研究不足与展望

  • AHP-RS组合权值法中经验因子的选取仍带有一定主观性，需进一步研究以提高其客观性；
  • 本文考虑的影响点群要素空间相似度计算的指标较为有限，未来研究还需考虑其他特征指标，并通过计算权值及权重排序选择更为合适的特征指标。