SimGNN多尺度建筑群组相似度计算方法
空间目标具有自身几何特征和相互之间的空间关系特征。本方法融合了空间关系与SimGNN模型,通过图级和节点级两种策略计算建筑群组相似度。
方法流程
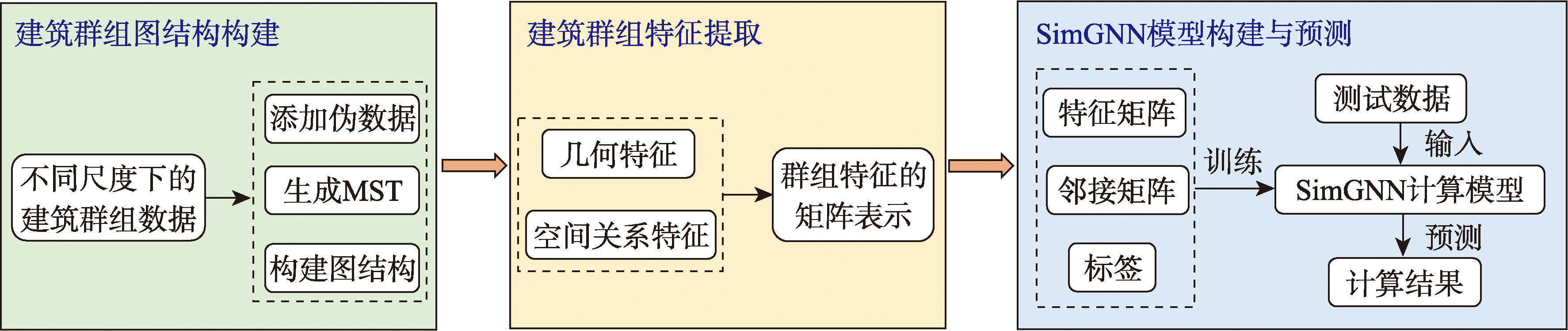
方法主要包括三个步骤:首先,由经验丰富的制图人员依据道路网等地理特征对大幅数据进行同区域划分,得到小区域建筑群组,同时通过添加伪数据节点以保持各建筑群组具有相同数目的建筑物,并对每个建筑群组构建图结构;然后,结合Gestalt原则选取特征描述指标,包含拓扑、方向、距离在内的空间关系特征及几何特征;最后,将图数据输入到模型中对其进行两种粒度级别的处理,从而得到群组间的相似度计算结果。
建筑群组图结构构建
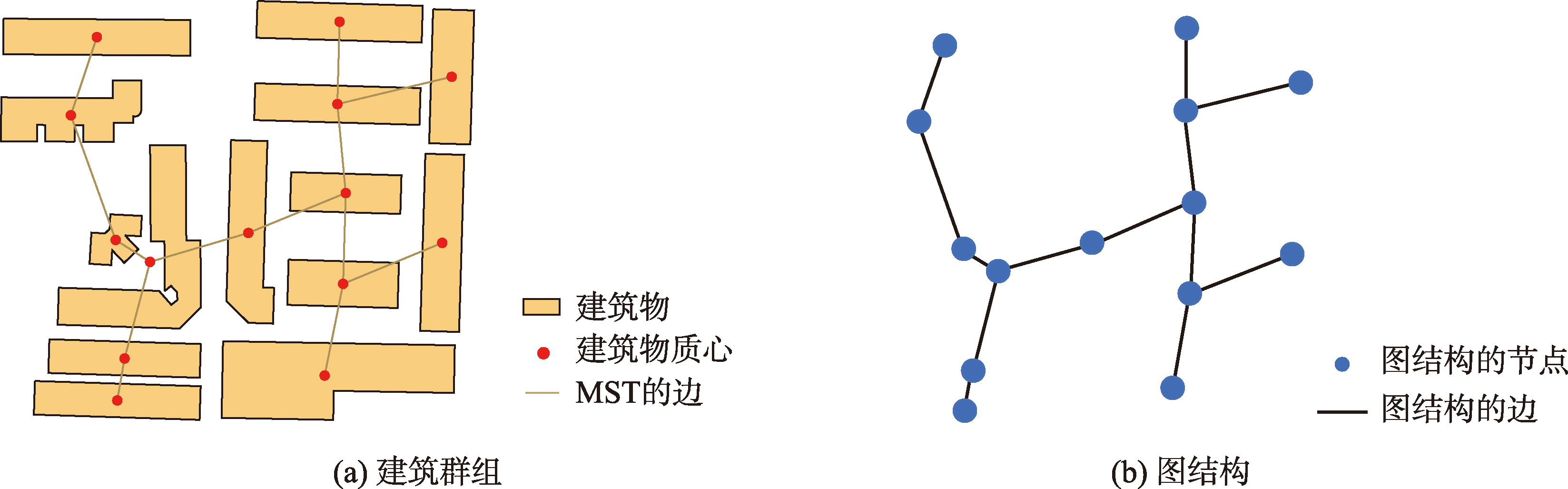
为了更好地表达和处理建筑群组中各建筑物之间的复杂关系,需要建立其图结构。首先,利用各建筑物的顶点坐标求出其质心,并作为图结构的节点;然后,连接各建筑物质心构建出MST(最小生成树),并将MST的边作为图结构的边,得到建筑群组的图结构。
建筑群组特征提取
几何特征
本文借鉴认知心理学中的格式塔原则,从视觉认知角度选取能够描述建筑物几何特征的因子,包括:
- 尺寸特征:面积、周长、均半径
- 形状特征:边数、紧凑度、延展度
- 密度特征:密度、实心度
- 方向特征:SMBR方向
空间关系特征
空间关系特征主要包括三种类型:
- 拓扑关系特征:采用邻近度特征因子描述建筑物之间的拓扑关系
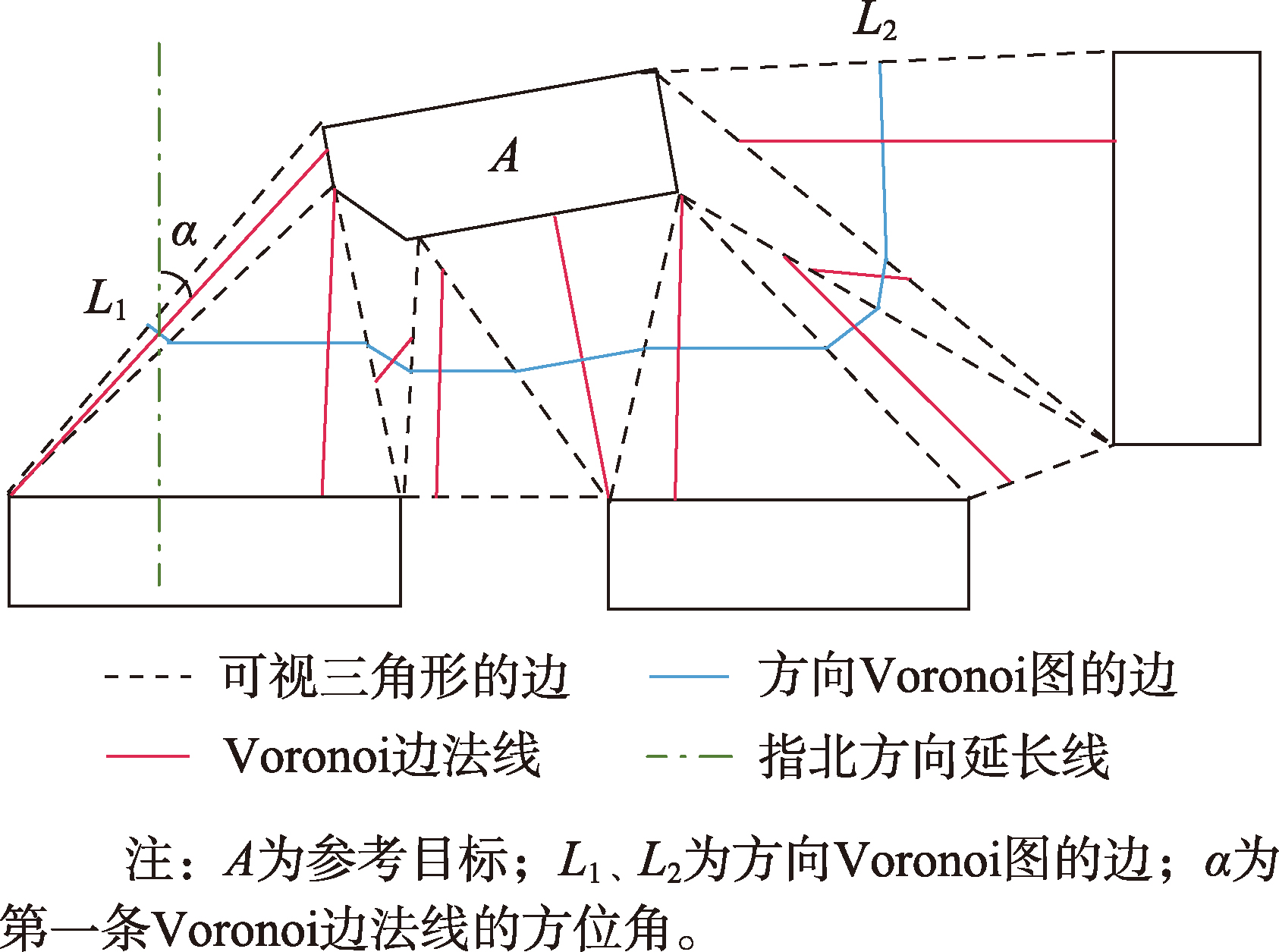
- 方向关系特征:采用方向Voronoi图模型描述建筑物与邻近目标集合间的方向关系
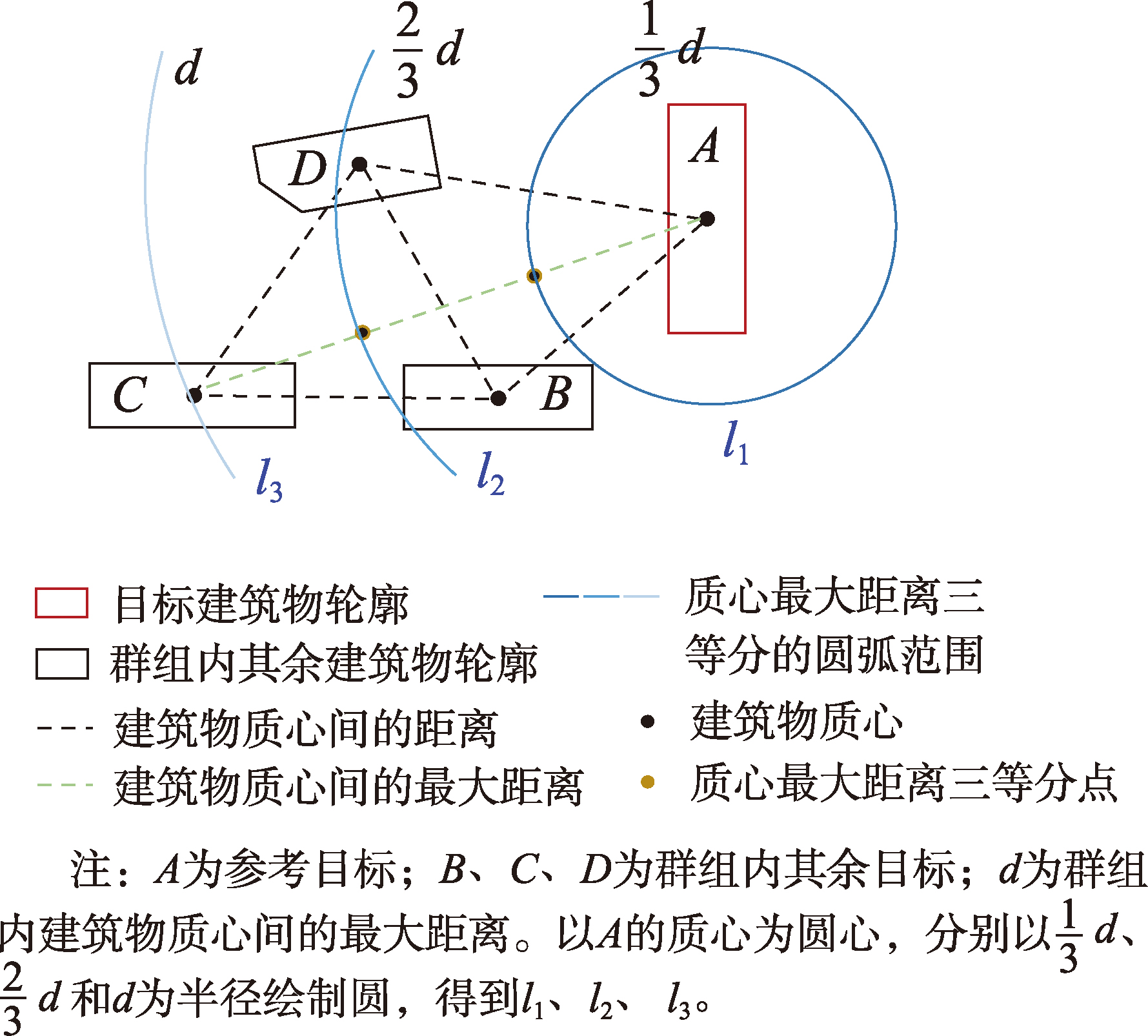
- 距离关系特征:选择质心距离作为建筑物间的距离关系特征
SimGNN模型构建与预测
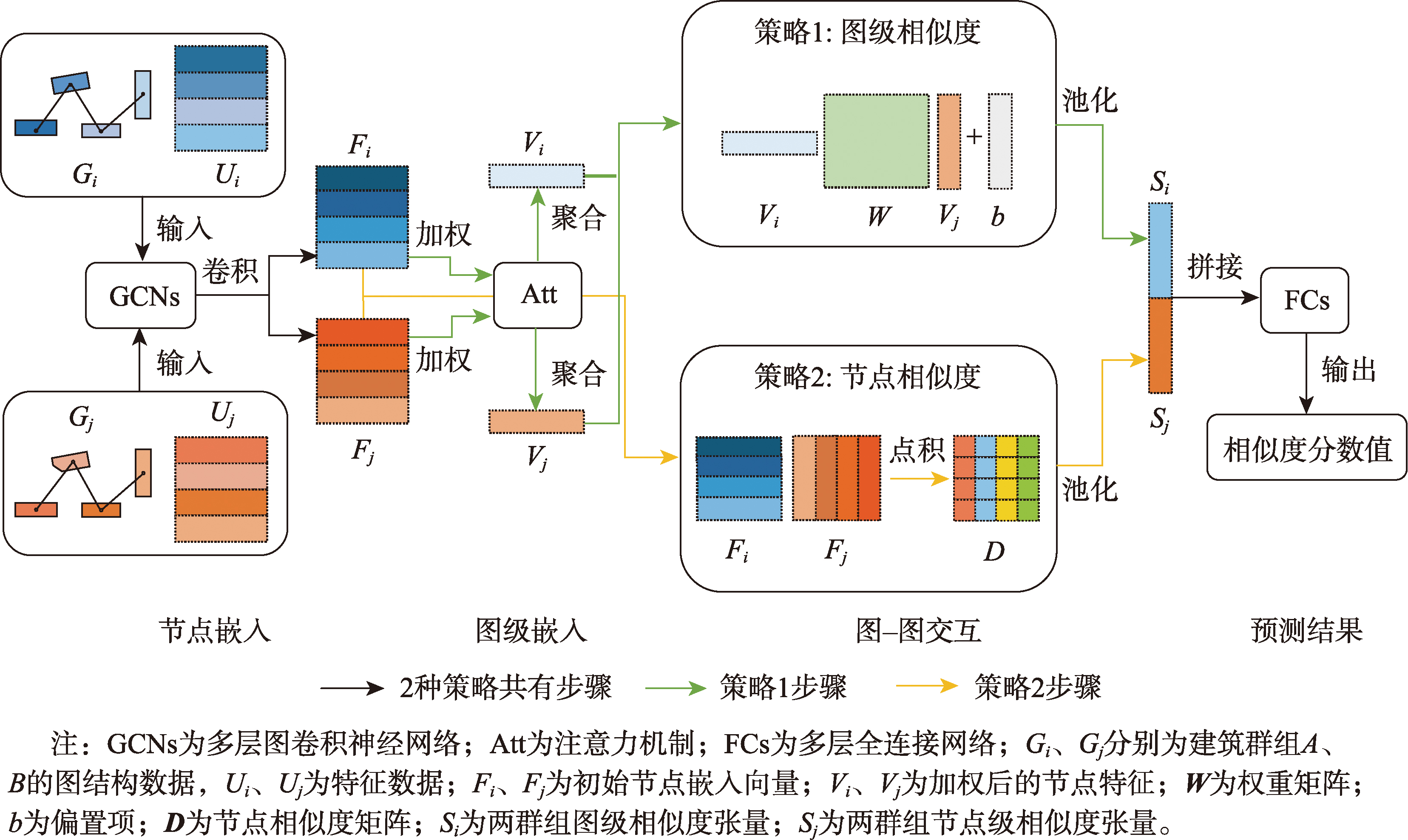
在很多情况下,两群组之间的差异仅体现在小的细节当中,很难通过图级编码反映出来。为此,SimGNN模型设计了细粒度成对节点比较策略,从中提取群组中各建筑物节点间的相似度信息,用以弥补图级比较策略的缺陷。
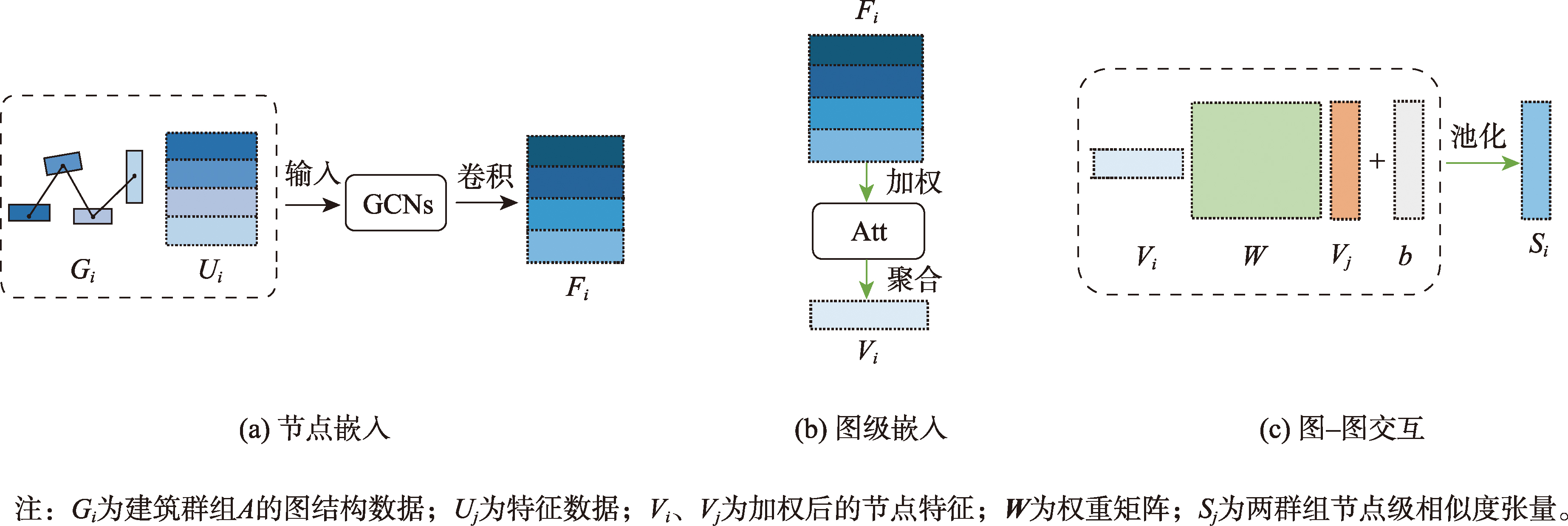
图级比较策略
在图级比较策略中,首先进行节点嵌入,使用GCN对每个节点特征和结构属性进行编码,得到初始节点嵌入向量;然后进行图级嵌入,应用注意力机制为每个节点嵌入分配权重,反映各节点在整个图中的重要性;最后在图-图交互阶段中,接收两幅图加权后的图级嵌入向量,得到图级相似度张量。
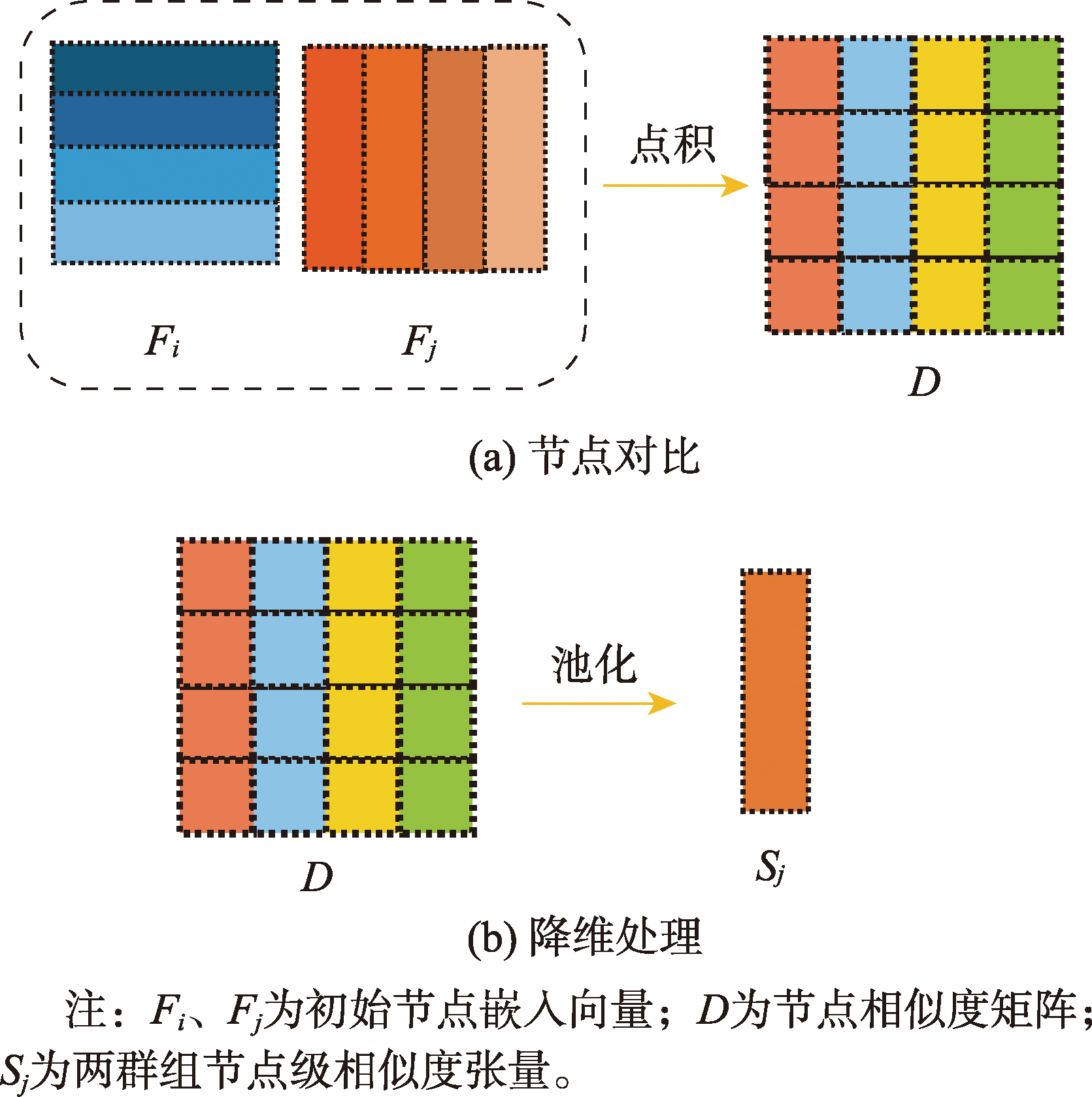
节点级比较策略
在节点级比较策略中,首先提取群组中所有节点嵌入,通过矩阵点积计算两群组中对应节点之间的相似度,得到配对节点相似度矩阵;然后对节点相似度矩阵中的值进行统计,得到节点相似度分布的频次向量,对该向量进行归一化后,得到节点相似度张量。
实验与分析
本研究采用Python语言,借助PyTorch深度学习框架与PyTorch Geometric图神经网络库搭建SimGNN模型,并在Microsoft Win10/64位操作系统、NVIDIA GeForce GTX 1650(GPU)的硬件平台上进行实验。
数据来源与处理
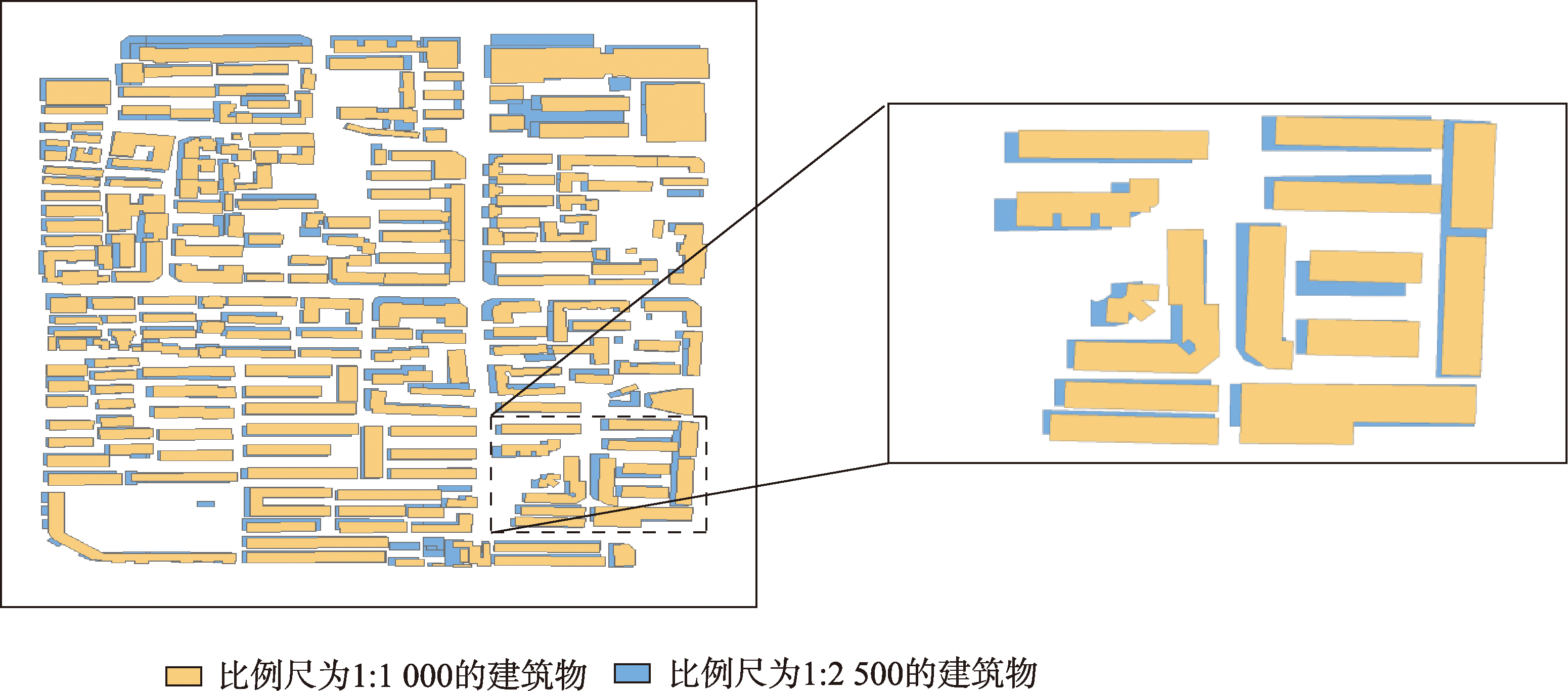
本实验选用西安市中心城区的面状建筑群组进行实验,建筑群组数据来源于百度地图。选用具有高精度信息的4个大比例尺矢量数据集:基础原始数据比例尺为1:1 000,待比较数据比例尺分别为1:2 500、1:5 000及1:10 000。
实验通过自监督学习来训练模型,利用输入数据本身的结构和特征属性信息来生成"数据驱动标签",而不使用外部标签信息。选取特征完全相似的500对建筑群组作为正样本数据,标签为1;选取不同区域无对应关系的500对建筑群组作为负样本数据,标签为0。训练集和验证集按8:2的比率划分。
相似度计算实验
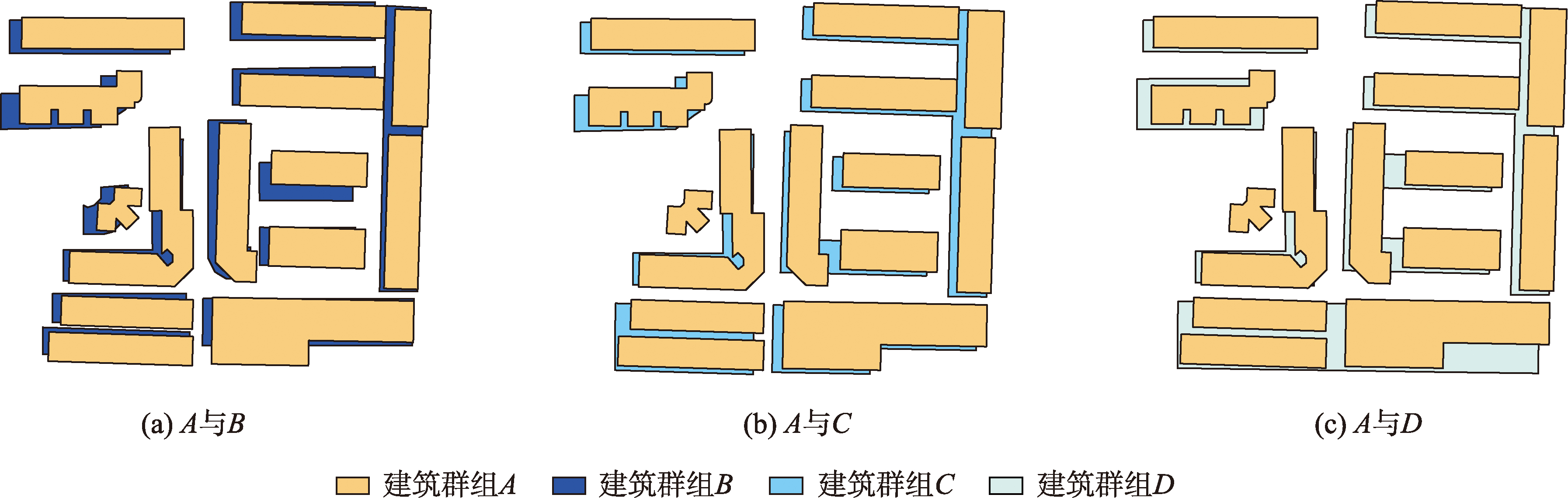
本文选取比例尺为1:1 000的建筑群组A作为标准数据,比例尺为1:2 500的建筑群组B、1:5 000的建筑群组C及1:10 000的建筑群组D作为待比较数据进行相似度计算实验。
| 建筑群组对 | 特征相似度分布 | 节点相似度分布 | 相似度分数 |
|---|---|---|---|
| A&B | [0.000, 0.000, 0.417, 0.583] | [0.077, 0.230, 0.231, 0.462] | 0.912 |
| A&C | [0.000, 0.167, 0.333, 0.500] | [0.111, 0.333, 0.222, 0.334] | 0.835 |
| A&D | [0.333, 0.167, 0.500, 0.000] | [0.500, 0.333, 0.167, 0.000] | 0.726 |
特征相似度与节点相似度分析
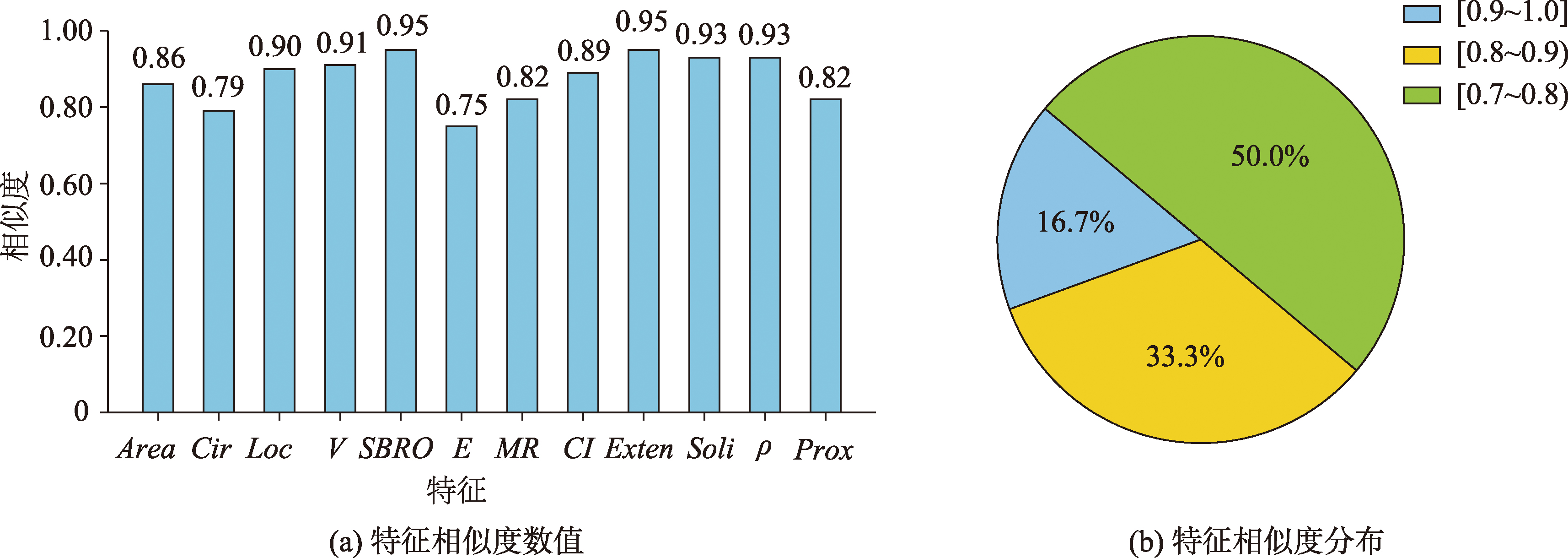
随着比例尺的缩小,各项特征的相似度逐渐降低,相似度分布从[0.9, 1.0]、[0.8, 0.9)逐渐向低值区间迁移。其中,建筑物的边数、周长及邻近度的相似度相对较低,这可归因于比例尺缩小过程中,建筑物的部分细节缺失以及相邻建筑物的合并所导致的特征信息损失。
节点相似度分析
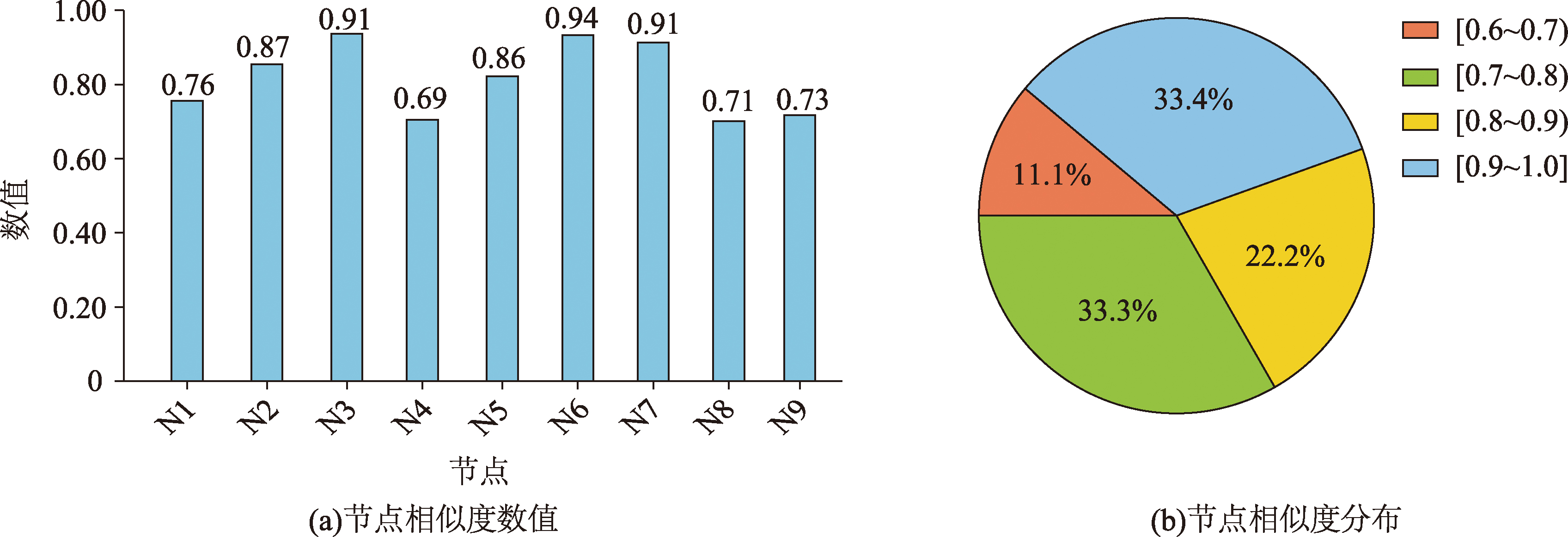
各节点的相似度随比例尺的缩小呈现逐渐降低的趋势。相似度最低的节点为N1、N4、N8、N9,这说明相应的建筑物在尺度缩小时相似度的变化最大,可能进行了合并、删除等操作。
模型对比实验
不同方法的相似度计算结果
| 方法 | A&B | A&C | A&D |
|---|---|---|---|
| 主观权重法 | 0.934 | 0.873 | 0.802 |
| VGCAE | 0.926 | 0.892 | 0.864 |
| DGCNN | 0.901 | 0.816 | 0.693 |
| SimGNN | 0.912 | 0.835 | 0.726 |
主观权重法虽在A&B群组上表现良好,但受人为设定权重的主观性影响,在A&D群组上的评分偏高,未能完全反映受访者的认知差异。VGCAE模型因选取的特征较少,在A&D群组上评分偏高,难以捕捉目标之间的细微差异。DGCNN模型选取的形状因子较多,比例尺变换导致建筑物形状变化显著,从而得出的相似度整体偏低。
心理认知实验结果
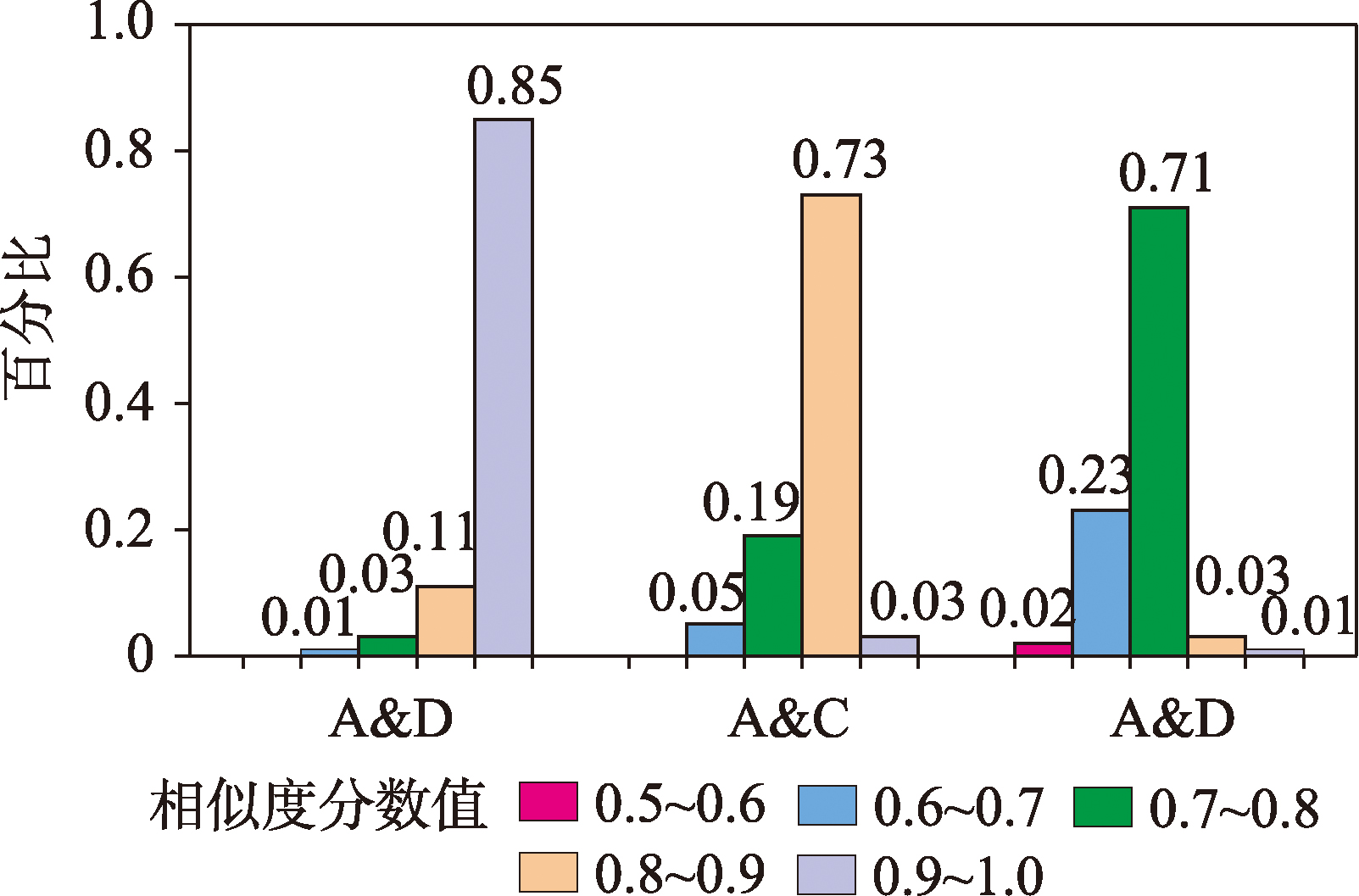
为检验计算结果是否与人们的认知相符,随机选取300位受访者进行心理认知实验,让每位受访者对3对建筑群组的相似度打分。对比实验结果可知,本文模型得出的相似度与心理认知实验结果契合度较高。在A&B群组上准确反映高相似度,A&C群组评分适中,在A&D群组上,SimGNN评分与受访者普遍的低相似度认知高度一致,进一步表明本文方法在不同尺度下衡量建筑群组间的相似度具有更好的效果。
结论与讨论
综合特征分析
本文综合建筑群组的几何特征和空间关系特征进行相似度计算,随着比例尺的缩小,群组总相似度从0.912降至0.726。与仅考虑建筑群组几何特征的模型相比,得到的相似度更符合人们的认知。
双策略处理
本文在图级处理群组上下文信息的基础上,顾及到局部细节的差异性,模型利用图级和细粒度节点级两种策略计算建筑群组的各项特征,通过细粒度节点级比较,得出建筑群组内各目标和各项特征的相似度分布。
自监督训练
相较于传统几何方法,本文通过深度学习模型的自监督训练实现了权值的自动生成,减少了人为干预,有效地避免了主观分配权重的不足,提升了多尺度建筑群组相似度的计算精度。
- 本文模型虽然借助细粒度节点级比较,反映出了群组之间的细微差异,但是在处理大规模的建筑群组时计算复杂度较高。
- 本文模型在计算相似度时仅考虑了建筑群组的几何特征和空间关系特征,未能顾及建筑物的语义信息,这一不足可能在某些特定应用场景中会限制模型的适用性。
综上,本文模型在计算效率和特征维度的完整性上仍存在改进空间,未来的研究工作将围绕这两个方面展开,以优化模型的性能,进一步提高其适用性。该模型有助于提升建筑群组相似检索、识别及匹配等空间数据处理方法的合理性和可靠性。