1 引言
空间分布模式是一种重要的空间结构特征,是地理要素在一定空间分布范围内表现出的可以明确命名且能够识别的形状或排列。建筑物是地图表达的基础地理要素,城市区域地图由建成区内的多个街区组成,街区中包含诸多的建筑物,而建筑物群组模式介于街区和建筑物实体之间,是城市结构和功能的重要组成部分。因此,如何自动、准确识别建筑物群组模式是城市空间理解、制图综合等领域的研究热点和难点问题。
现有研究主要基于格式塔原则,认为满足空间邻近、几何相似和分布连续的建筑物群组在视觉上更容易被归为整体构造,即空间分布模式,后文简称模式。建筑物群组模式的科学划分和准确描述是展开自动识别任务的基础,已有建筑物群组模式包括直线型、曲线型、网格型、规则与不规则型以及字母型等。直线模式是建筑物群组最简洁、最直接的模式,也是其他建筑物群组模式识别的基础,因此倍受关注。
建筑物群组模式识别需要在空间邻近关系建立的基础上进行,通常采用邻近图表达建筑物的属性及其相互关系。建筑物邻近图建立方式包含多种形式,例如Delaunay三角网(Delaunay triangulation,DT)、最小生成树(minimum spanning tree,MST)和Gabriel图等。
2 研究方法
2.1 总体框架
本文方法的框架如图1所示,主要包括以下4个步骤:
- 利用街区对建筑物进行分组,并对分组后的建筑物群组进行模式类别标注
- 分别引入邻近图和对偶图2类6种图结构对建筑物群组及其邻近关系进行图结构化表达
- 引入尺寸、方向、形状和密度共4类10种指标描述邻近图节点特征,融合相似性判断的领域知识,引入尺寸相似度、方向相似度、形状相似度、密度相似度和位置相似度共5类11种指标描述对偶图节点特征,得到建筑物群组图数据集
- 设计基于GraphSAGE的建筑物群组模式图分类模型架构,利用训练集对其进行训练、测试集进行测试,并对模式分类结果进行评价
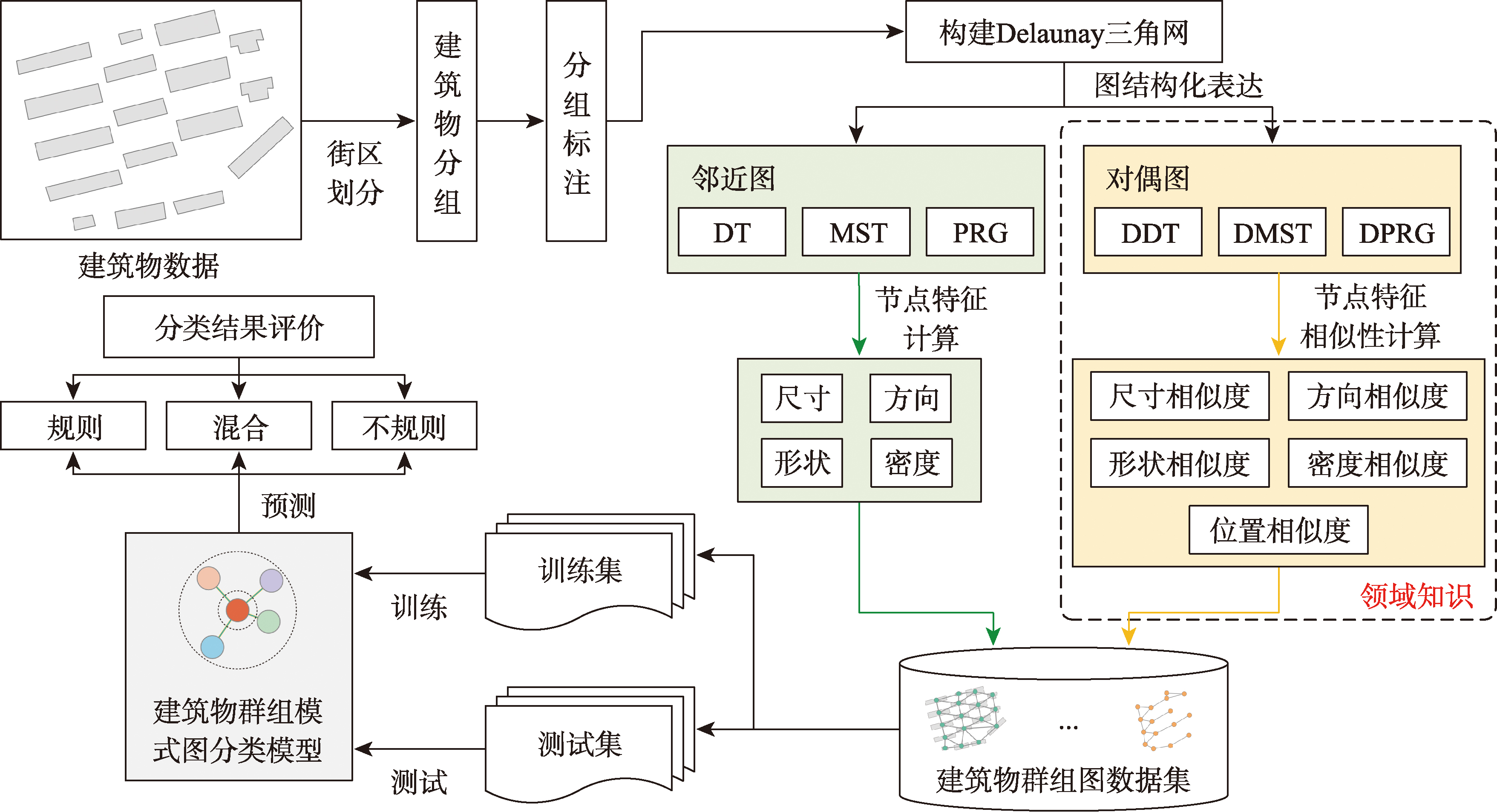
图1 融合领域知识的建筑物群组模式自动分类框架
2.2 数据集构建与标注
建筑物作为典型的人工地理要素,在大比例尺地图空间,采用直角转折的多边形表示其图上分布范围,随着比例尺的缩小,相互邻近的建筑物逐渐概化为新的多边形表示。
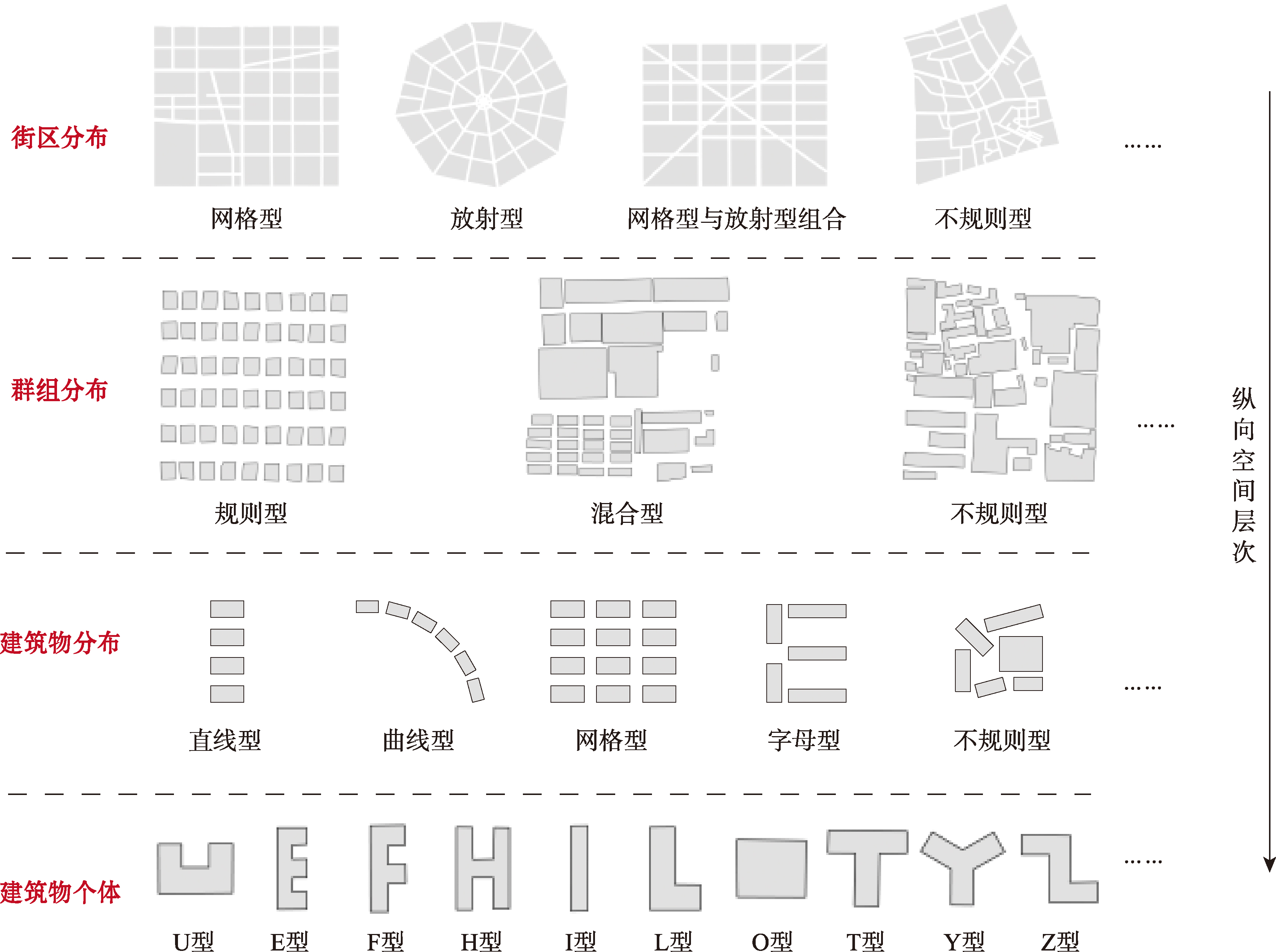
图2 建筑物空间层次划分
本研究以建筑物群组多尺度表达和制图综合的需求为牵引,面向街区内建筑物群组分布层次,对建筑物群组规则、混合和不规则3类模式进行自动分类研究(表1),以保持在此基础上建筑物制图综合结果的空间结构特征。
| 类别 | 图示描述 | 标签 | 制图综合方式 |
|---|---|---|---|
| 规则 | 规则建筑物群组中的建筑物在排列上较为同质,如直线和格网排列等,同排列内建筑物形状相似 | [1, 0, 0] | 按模式典型化 |
| 混合 | 混合建筑物群组介于规则与不规则之间,同时包含同质排列与错乱排列 | [0, 1, 0] | 先聚类分割,后典型化或聚合 |
| 不规则 | 不规则建筑物群组中的建筑物排列错乱,形态各异 | [0, 0, 1] | 聚合 |
以上海市作为研究区域(图3),首先获取其OSM道路网数据和建筑物实体数据,统一数学基础并预处理;其次,利用OSM道路网生成的道路网眼单元作为街区划分的基础,并通过人机交互编辑生成街区多边形(合计3 808个);然后,利用街区多边形对建筑物实体数据进行裁剪,获取街区多边形包含的建筑物群组;最后,将建筑物群组划分为实验数据集(3 148个)和讨论数据集(660个)2类。

图3 研究区域的建筑物群组划分情况
| 类别 | 建筑物群组数 | 建筑物数 | 组内建筑物数平均值 | 组内建筑物数最大值 | 组内建筑物数最小值 | 组内建筑物数中位数 |
|---|---|---|---|---|---|---|
| 规则 | 693 | 21 591 | 31.2 | 476 | 5 | 20 |
| 混合 | 1 661 | 65 953 | 39.7 | 284 | 9 | 34 |
| 不规则 | 794 | 19 485 | 24.5 | 328 | 4 | 20 |
| 总计 | 3 148 | 107 029 | 34.0 | 476 | 4 | 27 |
2.3 图结构化表达
邻近关系的图结构化表达是应用图神经网络方法进行建筑物群组模式分类的基础。本研究通过基于Delaunay三角网的邻近分析获取建筑物之间的邻近关系,首先对加密后的建筑物群组构建约束型Delaunay三角网(Constrained Delaunay Triangulation,CDT),其次连接不同建筑物之间的三角形骨架线,得到建筑物的Voronoi图剖分(图4(b)),各个Voronoi图单元之间的邻近关系即为其所包含建筑物之间的邻近关系(图4(c)),边权重为相邻建筑物之间的最短距离,记为DT。DT应用图论中的最小生成树算法,可以得到另一种图结构MST(图4(d))。
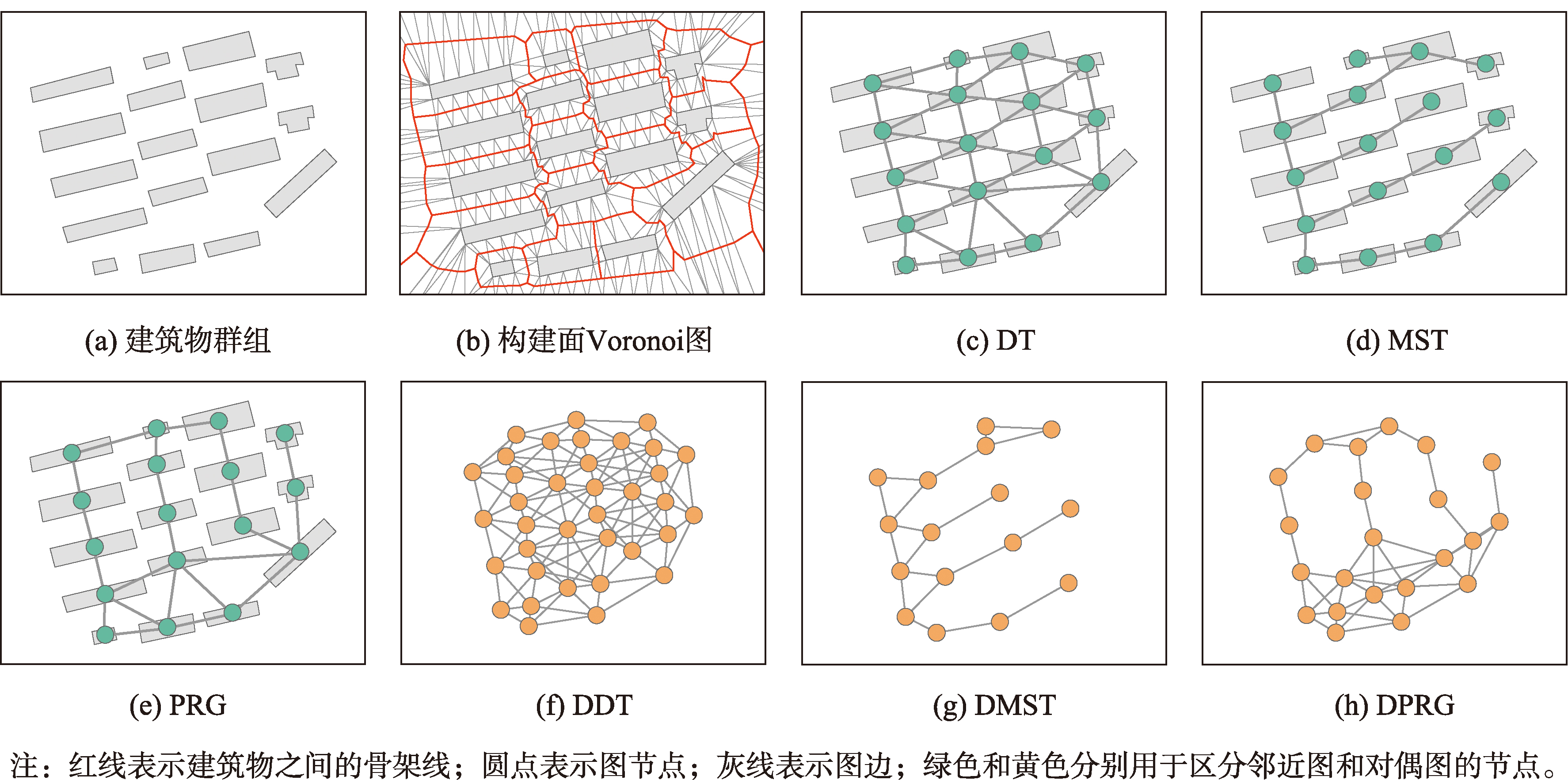
图4 建筑物群组图结构化表达过程
2.4 图节点特征描述
| 邻近图 | 特征类别 | 特征指标 | 描述/计算公式 |
|---|---|---|---|
| 尺寸 | 周长L | 建筑物所有顶点到其质心的平均距离 | |
| 面积S | |||
| 均半径MR | |||
| 方向 | x轴倾向Ox | 图5(a)的夹角Ox | |
| y轴倾向Oy | 图5(a)的夹角Oy | ||
| 形状 | 紧凑度Cir | Cir=4πS/L² | |
| 偏心率Ecc | Ecc=a/b,a为建筑物SBR短轴长度,b为长轴长度 | ||
| 凹度Con | Con=S/Sc,Sc为建筑物凸包的面积 | ||
| 矩形度Rec | Rec=S/SR,SR为建筑物MBR的面积 | ||
| 密度 | 密度Den | Den=S/SV,SV为建筑物Voronoi图的面积 |
规则模式内各建筑物在尺寸、方向、形状、密度和距离等方面"相似",而不规则模式内各建筑物则显著"不相似"。传统基于规则的建筑物群组模式识别方法,通过判断局部建筑物之间是否相似来逐步得到整体模式分类结果,符合从局部到整体的视觉认知过程。
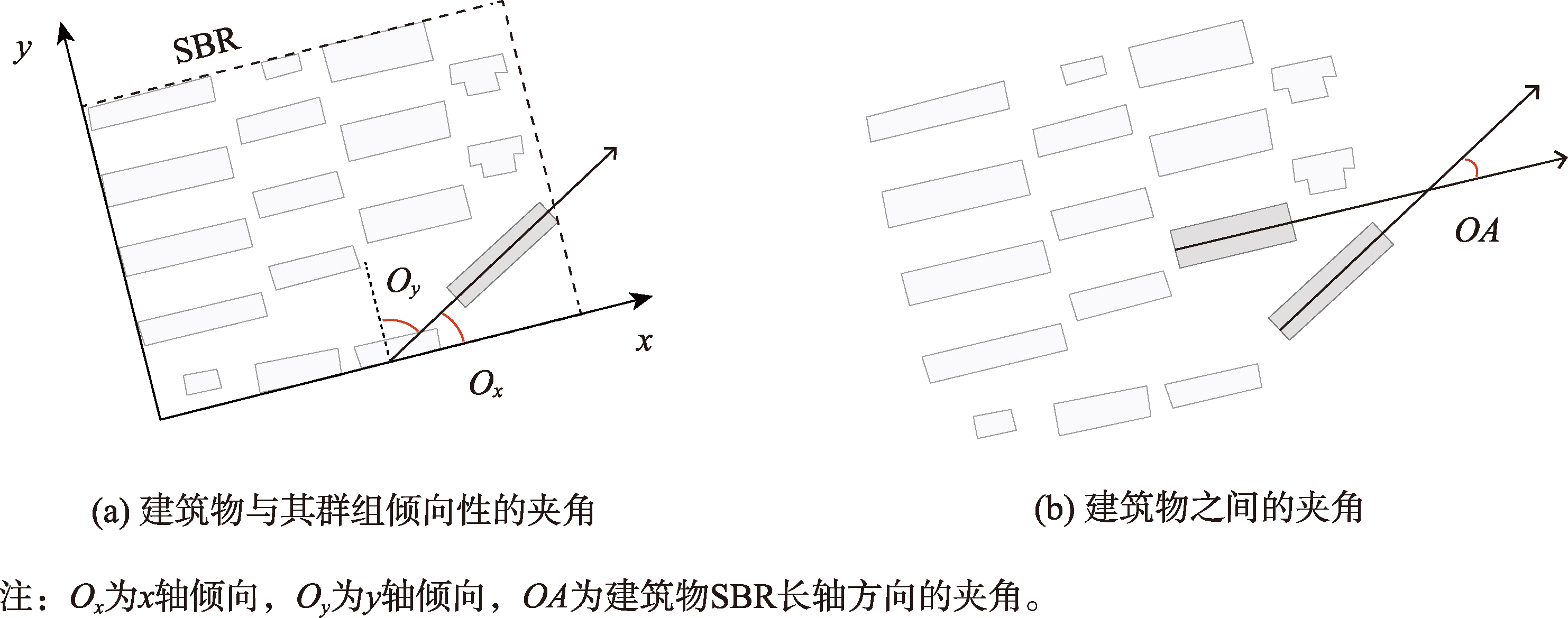
图5 方向与方向相似度计算示意
3 实验结果与分析
为了验证不同图结构及其包含特征对建筑物群组模式分类的有效性,分别将2.3节中的6种图结构及其在2.4节提取的节点特征输入到GSN-BGPC进行分类训练和测试。实验设置GSN-BGPC的隐藏层数为2、嵌入特征维度为64,考虑到初始化权重对模型训练结果的影响,每种图结构分别训练20次,然后统计每一次的验证和测试准确率。
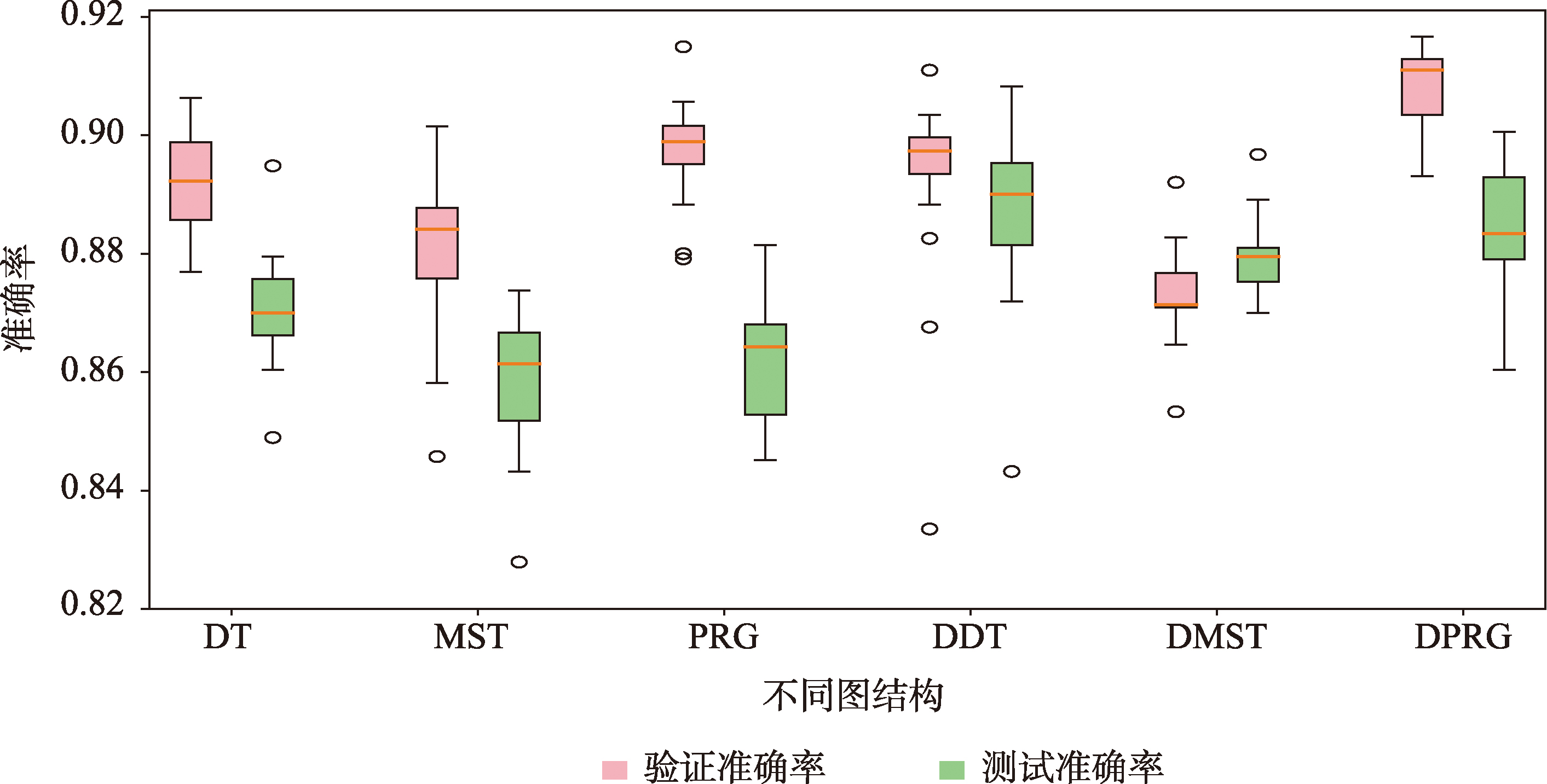
图6 不同图结构的建筑物群组模式分类效果
选择合适的超参数对提高模型性能很重要,为此进一步比较GSN-BGPC的隐藏层数(HL)与嵌入特征维度(ED)对建筑物群组分类精度的影响。采用控制变量法确定最优的参数设置,GSN-BGPC模型的HL分别设置为1、2、3、4、5和6,ED分别设置为8、16、32、64、128、256和512,共计得到42组超参数组合。
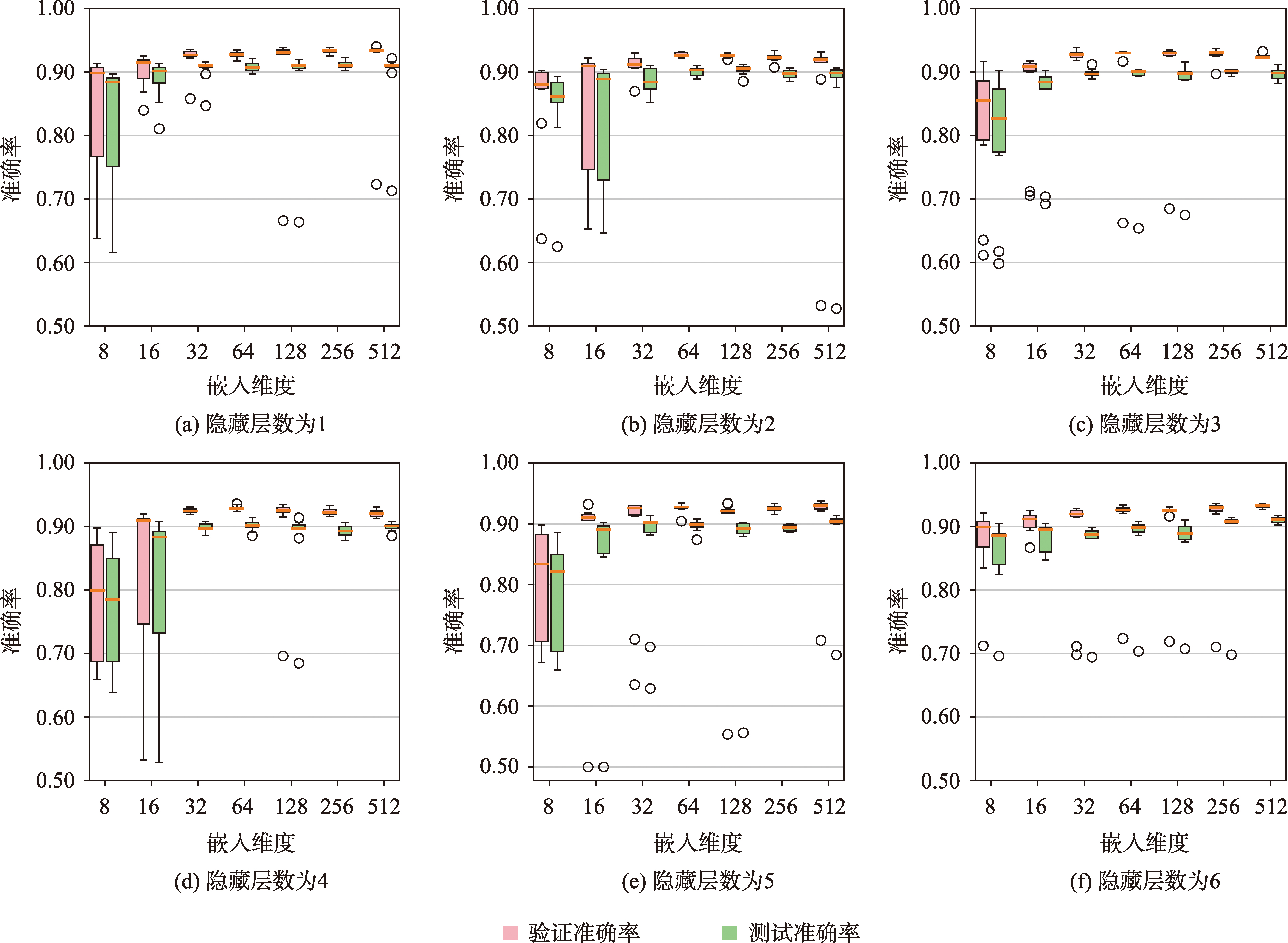
图7 GSN-BGPC不同超参数的建筑物群组模式分类效果
特征的有效选取是提高深度学习模型性能的重要方面。为了验证11个相似度特征的有效性及其对建筑物群组模式分类的贡献,分别设计了2组对比实验:①从11个相似度特征中依次舍弃其中1个特征;②仅考虑其中的1个特征,分别得到26组输入GSN-BGPC的特征组合(表5)。
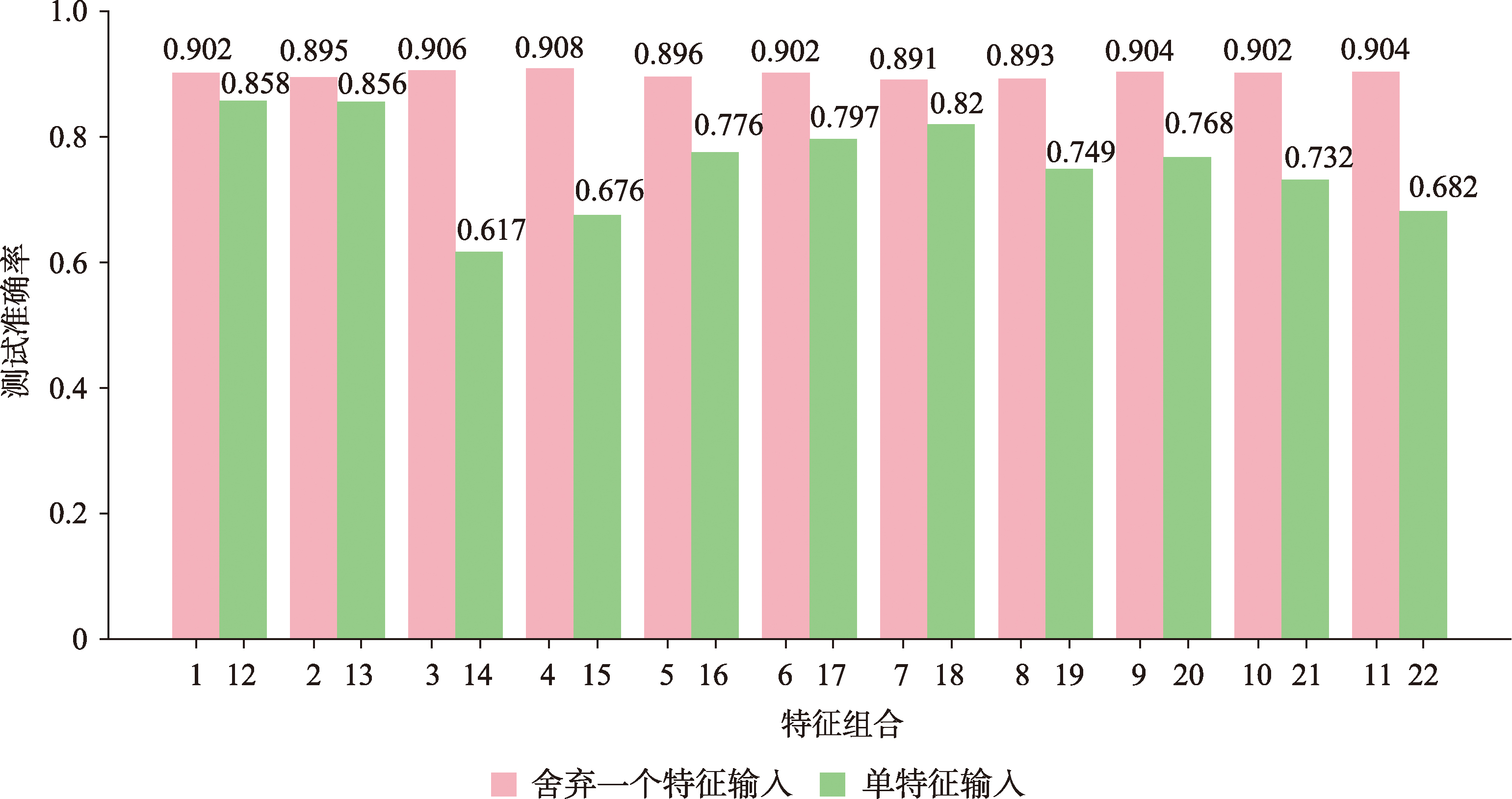
图8 不同特征组合的建筑物群组模式分类效果
进一步比较基于邻近图的特征指标与基于对偶图的相似性特征指标对提升模型性能的贡献,分别基于3种邻近图结构,依次输入10种邻近图特征进行训练。测试结果如图11所示,分析可知,基于PRG图结构明显优于其他2种邻近图结构,部分特征也优于基于DPRG图结构的相似度特征,其他特征则相当或不足。
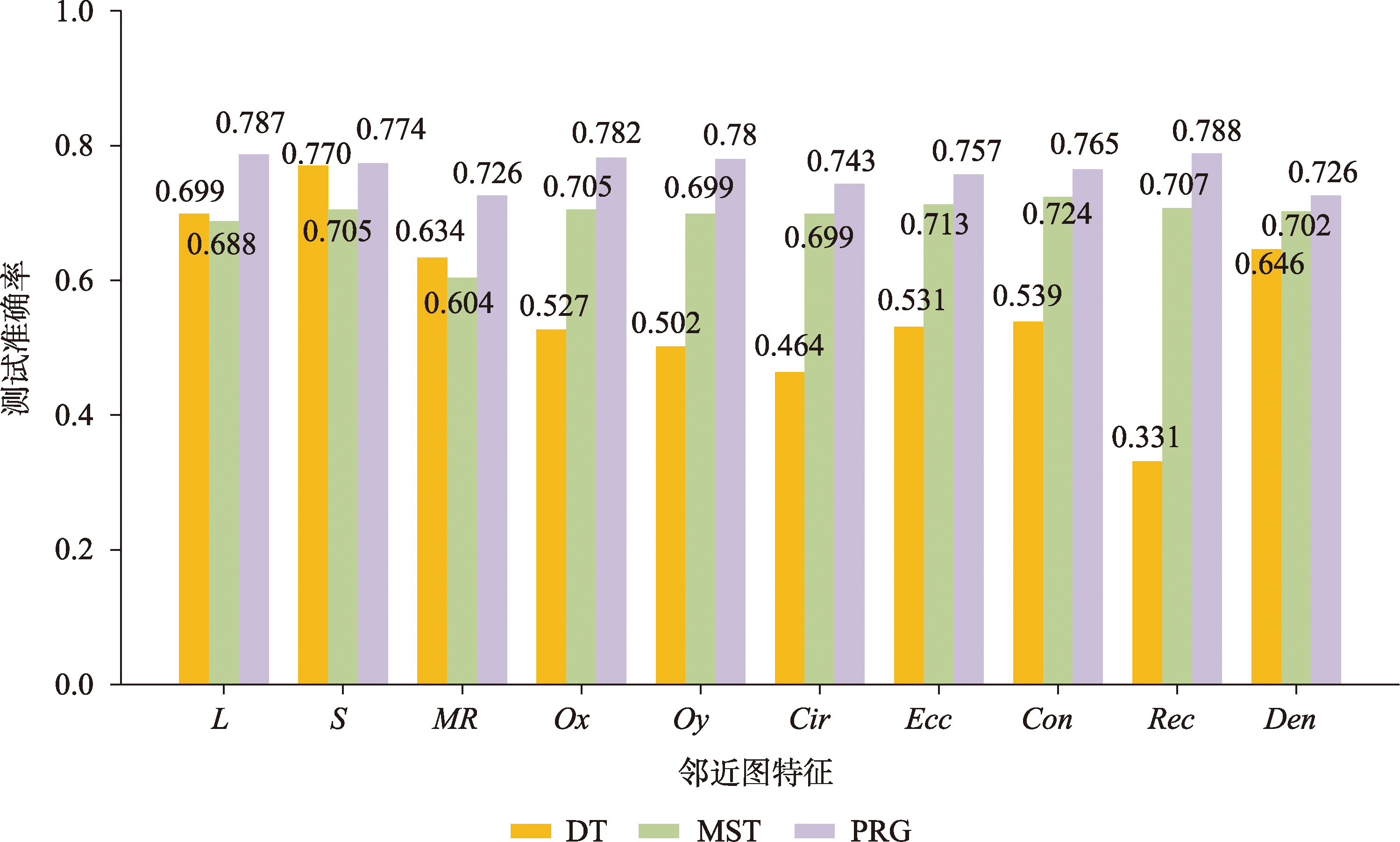
图9 不同邻近图特征的建筑物群组模式分类效果
结论与讨论
4.1 结论
建筑物群组模式介于街区和建筑物实体之间,是城市结构和功能的重要组成部分,其自动识别结果可以应用于城市规划与分析、城市区域制图综合等应用中。针对现有建筑物群组模式分类研究具有简单性(规则与不规则的二分类)和特定性(引入直线、网格等特定模式,对建筑物群组的预处理要求较高)的问题,本文在已有研究基础上,提出了一种融合领域知识的建筑物群组模式自动分类方法,以上海市街区建筑物群组数据为例,得出结论如下:
- 以建筑物多尺度表达和制图综合的需求为牵引,面向街区内建筑物群组分布层次,在规则与不规则模式之间增加了混合模式类别,进一步细化建筑物群组模式分类的粒度,并通过按模式综合验证了模式类别分类的合理性和可应用性
- 结合视觉认知特点和传统规则算法相似性判断的领域知识,设计了一种正对投影对偶图结构及其节点相似性特征描述,并验证了其相较于常用的建筑物邻近图结构,可以进一步提高模式分类的精度
- 引入GraphSAGE构建了建筑物群组模式自动分类模型,测试集准确率达到91.2%,相较于已有方法准确率提高了9.0%,且该模型相较于GCN和GAT模型,准确率分别提高了3.6%和4.6%,规则与不规则模式的二分类准确率达到98.4%
4.2 讨论
本文方法虽然在规则、混合和不规则街区建筑物群组模式分类中取得了一定的成果,但是仍存在一些问题有待优化:
- 街区内建筑物的数量对GSN-BGPC模型识别精度有消极影响,如模型不易区分由少数几个建筑物组成的群组模式,需要进一步加入判断规则辅助区分
- 建筑物群组模式与组成其的建筑物形状有紧密联系,然而常用的形状数值指标对模型分类精度提升有限,因此,后续考虑采用形状的向量指标,以提高模型的识别精度
- GSN-BGPC模型不能实现对混合模式中局部规则和不规则建筑物群组子模式的自动分割,限制了模式分类结果的进一步应用,因此,下一步考虑引入图节点分类模型,解决建筑物群组子模式的自动分割问题
* 以上内容由AI自动生成,内容仅供参考。对于因使用本网站以上内容产生的相关后果,本网站不承担任何商业和法律责任。