训练样本采样优化与机器学习结合的滑坡易发性评价方法

1 引言

我国幅员辽阔，涵盖复杂多样的地质结构，是世界上受滑坡灾害影响最严重的国家之一。滑坡灾害易发性评价是以地质环境条件为基础，结合滑坡灾害孕灾因子和诱发因子预测其在一定区域内发生的可能性大小，其意义是在于评价特定地区发生滑坡灾害的可能性，从理论上可理解为对于未知区域的空间预测，对于潜在灾害危害点的时间预报，从而为滑坡灾害治理提供更加客观准确的信息支持，对区域地质灾害的防灾减灾规划具有重要意义。

国内外关于滑坡易发性评估的常见模型可分为经验模型、数理统计模型与机器学习模型 3 类。经验模模型中，层次分析法等虽然计算简单，但主观性强。数理统计模型中，证据权法、确定性系数法等能够将灾害与单一影响因子各区间的关系量化，但难以描述因子组合间的关联特征以及在高维空间中与灾害点的关系。近年来，随着大数据等相关技术的发展，大量学者将机器学习模型引入灾害易发性评价研究中，机器学习模型受数据驱动，在假设滑坡易发性与环境变量之间存在着协同变化的条件下，凭借其出色的高维非线性问题处理能力，综合每个评价单元的影响因子数据并计算其与滑坡灾害之间的关系，进而推测滑坡发生概率。

滑坡灾害影响因素

地形地貌特征
降水量及分布
地质结构与岩性
人类工程活动
水文条件
植被覆盖状况

常见机器学习模型有逻辑回归模型（LR）、随机森林（RF）、决策树（DT）、支持向量机（SVM）等。因不同模型对不同灾害样本数量的适用性不同，部分模型在小样本研究区域可能无法充分学习区域内的灾害发生规律和影响因素，产生过拟合等问题，已有学者开展对小样本区域采用机器学习模型进行滑坡易发性评价的可用性研究，发现 SVM 模型与其他模型相比在小样本数据相关研究中表现较好，具有较高的适用性，被认为是当前解决小样本数据分类问题和回归问题的最佳模型之一，更加适合样本数据有限的情况，同样，在集成学习算法中，RF(随机森林)模型已被广泛应用于各类灾害易发性评价研究中，在小样本数据预测处理方面也取得较好的结果。

训练样本数据集的构建质量对基于机器学习的滑坡易发性评价结果有着至关重要的影响，如何有效地构建用于机器学习训练的样本数据集是一个重要问题。训练样本数据分为正样本数据及负样本数据，正样本数据以历史滑坡编目数据为依据，在滑坡实际发生区域进行采样，其质量较高，能充分反映滑坡发生的典型地理环境条件，但对于小样本数据研究区域，有限的正样本可能难以反映区域的灾害特征；由于负样本的数量是基于正样本数量按一定比例提取的，两者构建的训练样本总数不足时也会限制模型对复杂地质环境的识别能力、性能和对未知数据的泛化能力。

综上所述，使用机器学习对小样本区域进行易发性评价时，训练样本的数量、空间分布以及数据质量会直接影响模型的性能与预测结果的准确度。为此，本文考虑结合多种机器学习模型进行数据扩充、特征筛选等操作，优化训练样本数据集，提升机器学习模型的泛化性和预测精度，尝试提出一种滑坡正样本扩充采样和采用无监督聚类模型进行客观提取相结合的训练样本数据采样优化方法。

2 研究思路与方法

训练样本采样优化与机器学习结合的滑坡易发性评价方法主要包括滑评价因子的筛选、采样优化样本数据集构建、基于机器学习的滑坡易发性评价模型构建3个部分。

图1 训练样本采样优化与机器学习结合的滑坡易发性评价技术路线

2.1 滑坡评价因子筛选

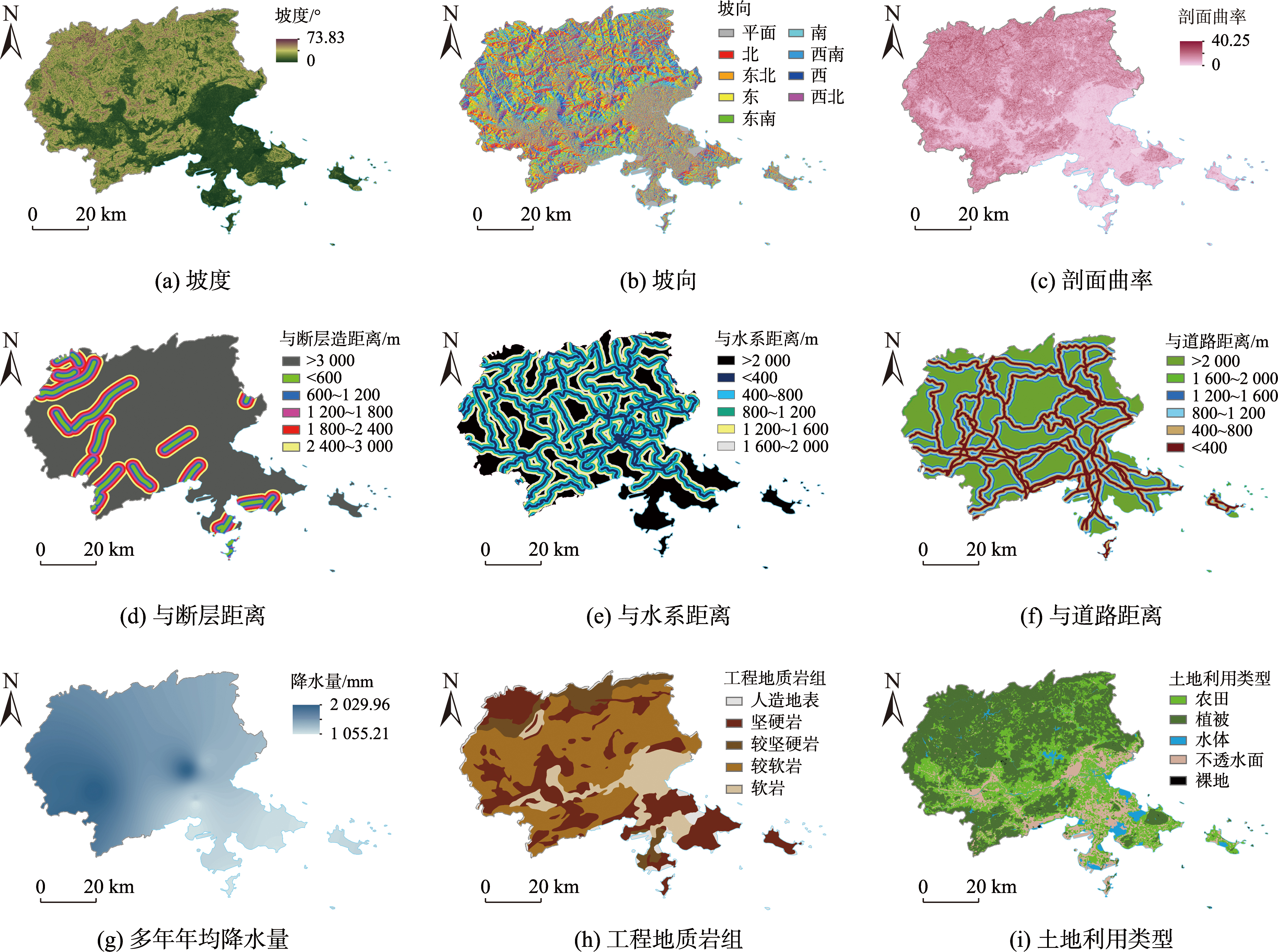
为提高模型预测的准确性，需要对评价影响因子同时进行相关性与共线性分析，并根据分析结果进行因子筛选，以保证评价因子的相互独立性。采用皮尔逊相关系数衡量因子之间的相关程度，当相关系数绝对值高于 0.4 时，认为因子间存在较高相关性，应予以剔除。共线性分析中，当 TOL 小于 0.10、VIF大于10时认为该因子共线性严重，应予以剔除。

2.2 采样优化训练样本数据集构建

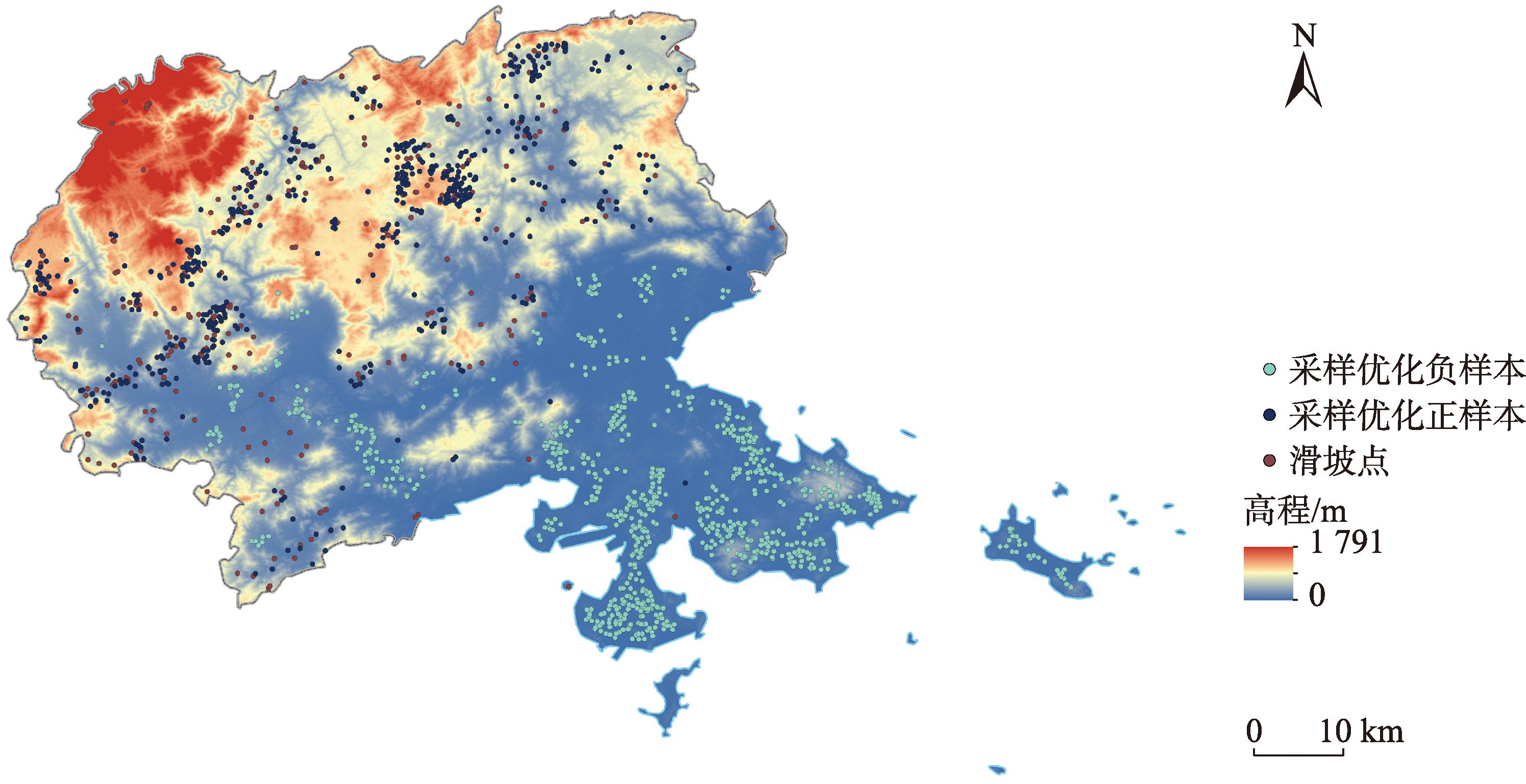
包括两个关键步骤：滑坡正样本数据筛选扩充和滑坡负样本数据客观提取。通过滑坡正样本原型采样方法（PBS）对正样本进行数据扩充，筛选捕捉滑坡发生的关键影响因素，获取更客观、更具代表性的正样本数据集；采用无监督聚类模型对负样本进行客观提取，在保留重要数据空间分布特征的同时降低引入噪声的干扰性，提高负样本数据集的质量。

2.2.1 滑坡正样本数据筛选扩充

筛选扩充滑坡正样本数据可以确保模型能够训练学习更多的滑坡特征信息。采用滑坡正样本原型采样方法（PBS），以滑坡空间分布点数据构建半径为1 km范围的缓冲区作为滑坡多边形，通过频率采集方法在滑坡多边形内提取滑坡正样本原型数据，构建滑坡正样本原型数据集，量化滑坡多边形内的样本数据与滑坡灾害之间的关系，捕捉滑坡发生的关键影响因素。

正样本原型数据集构建流程：

对滑坡多边形的每一个评价因子构建评价因子频率直方图
将评价因子值位于最大频率区间的像元点作为正样本原型
进行地理环境相似度计算
根据可信度阈值进行采样，保证正样本数据的客观性与可靠性

组距的建立采用如下经验公式：

bine = 2 × IQRe × n^-1/3

式中：bine是评价因子 e 的直方图组距；n 和 IQRe分别是评价因子e的点位数量和四分差。

对各评价因子按照所属数据类型分别进行地理环境相似度计算，分别采用频率比和核密度函数计算离散型和连续型评价因子与滑坡正样本原型数据发生频率之间的函数关系；对各评价因子相似度栅格数据进行计算，获得栅格数据与正样本原型数据的综合评价因子相似度。

2.2.2 滑坡负样本数据客观提取

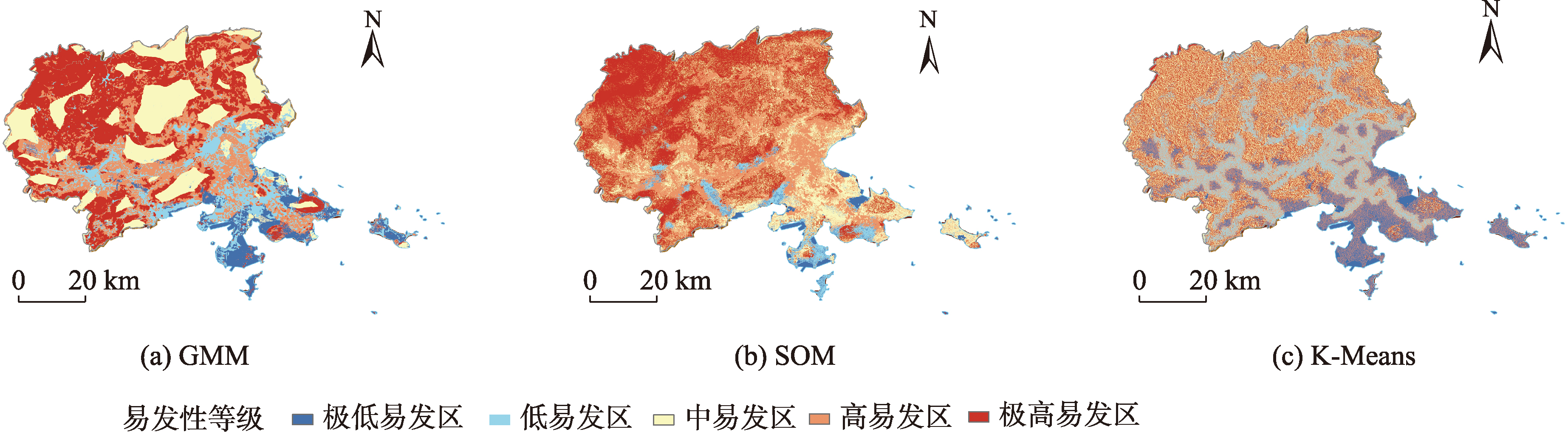
本研究采用无监督聚类效果较好的 K-Means聚类、高斯混合模型与自组织神经网络对滑坡负样本数据进行客观优化提取。通过无监督聚类模型对负样本进行提取，能够得到若干组聚类簇，既反映负样本数据的集中分布情况，又保留滑坡负样本数据的空间分布特征。这种客观提取方法避免了数据欠采样导致的信息丢失，同时在聚类过程中考虑了数据之间的相似性，避免了过采样引入的噪声干扰问题，提高负样本数据集的可信度与客观性。

K-Means聚类

K-Means 聚类是一种结合了聚类和欠采样的机器学习基本算法，在没有先验数据的情况下对原始数据进行预分类，并在完成后验信息后对分类结果进行验证，可以一定程度上克服简单欠采样和过采样的缺点。

高斯混合模型

该方法是一种引入了基于 K-Means 聚类的概率模型，选择具有最高概率值的标签类作为聚类的最终结果。在高斯混合聚类模型（GMM）中，每个高斯模型代表一个类，最终训练的概率是几个高斯模型的加权和。

自组织神经网络

自组织神经网络（SOM）模型是一种无导师、无监督、自组织的学习过程，SOM 的层次结构由输入层和竞争层组成。输入层接收输入样本信息并逐渐将其传递到竞争层，由竞争层对接收到的输入样本信息进行各种比较分析。

2.3 基于机器学习的滑坡易发性评价模型构建

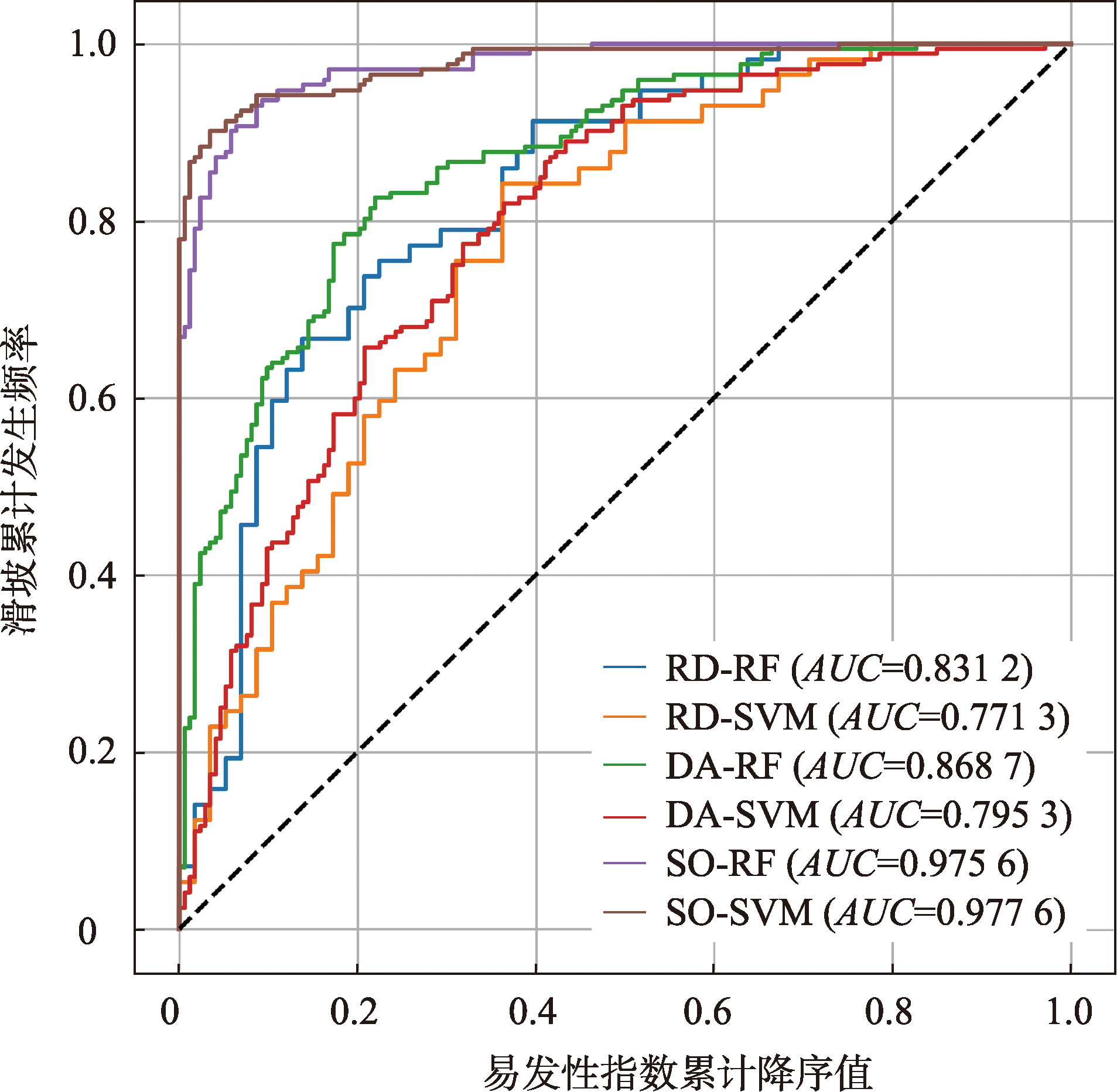
基于筛选后的评价因子组合，结合已知滑坡原始数据集及采样优化的训练样本数据集构成机器学习训练数据集，构建随机森林模型与支持向量机模型，利用网格搜索进行超参数调优，计算区域滑坡易发性指数，再通过ROC曲线对模型预测结果进行精度验证。最后，基于易发性预测结果进行滑坡危险性空间分布特征及其规律分析。

2.3.1 随机森林

随机森林（RF）是 bagging 算法的代表，由 Breiman于 2001年首次提出。它由多个决策树组成，在构建决策树时，对训练数据进行有放回的随机采样（一般选取总样本的 2/3），同时随机选取部分特征进行模型训练。其中，每次未被抽取的剩下 1/3 样本称为袋外数据（Out Of Bag，OOB），其误差可以用来验证模型的拟合性能。

P* ≤ ρ(1 - s²)/s²

式中：ρ为决策树之间的相关度平均值；s为决策树的平均强度。

2.3.2 支持向量机

支持向量机是一种建立在结构风险最小化和 VC 维理论基础之上的经典机器学习算法，对解决滑坡危险性评估存在非线性高维模式识别问题具备独特优势，比其他传统方法具有更好的评估能力与推广能力。

wx + b = 0

式中：w 表示法向量；x 表示超平面上的点；b 表示常数。当 w 和 b 达到最优时，所找到的最优超平面将使得正样本与负样本之间的距离最大。

3 实验区概况及数据源

3.1 实验区概况

本文以福建省莆田市为研究实验区域，莆田市地处福建沿海中部，地处24°59′N—25°46′N，118°27′E—119°56′E之间，北回归线北侧边缘，东濒海洋，属典型的亚热带海洋性季风气候。位于新华夏构造体系的长乐－南澳断裂带和第二带之上，由一系列呈 NE 走向且多期次的断裂破碎带、变质带、火山喷发带、岩体侵入带、岩脉及片麻理等构成，受该构造控制，区域内发生多起大规模构造运动。

莆田市区域内西北部多为中低山，中东部为低山、丘陵、平原，东南部沿海为半岛和岛屿，地势由西北向东南倾斜，坡体岩性为残坡积粘性土。降水年内年际变化大，全市各地年平均降水量在 1 000~2 300 mm 之间，降雨量自西北山区向东南沿海递减，5—9 月为雨季高发期，尤其是暴雨日次多，往往会造成局部强降雨而引发滑坡灾害。

莆田市滑坡灾害主要分布于西部与北部，根据资源环境科学与数据中心累积至 2019 年的地质灾害统计数据显示，莆田市历史滑坡灾害点有287 处，仅高于厦门（26 处），相较于福建其他地区，如南平市（1 009 个）、三明市（1 543个）等，属于典型的滑坡易发性评价小样本区域。

图2 莆田市滑坡点空间分布

莆田市地理特征

位于福建沿海中部
年均降水量1000~2300mm
西北部多为中低山
东南部沿海为半岛和岛屿
历史滑坡灾害点287处

3.2 数据来源及评价因子

滑坡易发性评价因子的筛选与构建是易发性评价研究的重要基础。本研究选取高程、坡度、坡向、剖面曲率、平面曲率、多年年均降水量、与断层距离、与水系距离、与道路距离、工程地质岩组、土地利用类型共 11 个滑坡易发性评价因子，各因子具体数据来源见表1。

表1 数据来源情况表

数据名称	数据来源	数据类型	数据时间/年	分辨率
数字高程影像	ASTER Global Digital Elevation Model V003	栅格	成像时间为2000年03月01日—2013年11月30日	30 m×30 m
地形数据	从数字高程影像提取	栅格	-	30 m×30 m
地质数据	地质科学数据出版系统1:100万福建省地质图数据	矢量	2017年	-
土地利用类型数据	1990—2021年中国30 m年土地覆被数据集	栅格	2020年	30 m×30 m
滑坡空间分布数据	资源环境科学与数据中心	矢量	积累至2019年	-
莆田市气象站点数据	中国国家气象局	文本	2019年	-
全国矢量数据文件(道路、河流等)	国家基础地理信息中心	矢量	2021年	-

图3 滑坡易发性评价因子

根据实验区所处地理位置，以及过往学者对福建省区域滑坡灾害评价因子筛选研究，降雨作为滑坡灾害主要诱发因素，故保留多年年均降雨因子；根据莆田市区域地理环境情况，多雨且小型土质滑坡较多，易受坡度直接影响，平面曲率虽同时具有反映一定地形信息的能力，但其对滑坡的直接影响不如坡度明显，故剔除平面曲率因子，保留坡度因子。因此，本研究筛选获得滑坡易发性评价因子为多年年均降水量、坡度、坡向、与断层距离、与水系距离、与道路距离、剖面曲率、工程地质岩组、土地利用类型共9个。

4 滑坡易发性评价模型构建与分析

4.1 采样优化的样本数据集构建

4.1.1 滑坡正样本数据集

通过构建滑坡多边形，结合频率采集方法获取滑坡正样本原型数据。对已知滑坡点进行缓冲区分析，将滑坡点半径1 km范围缓冲区作为滑坡多边形，并提取滑坡多边形内所有评价因子数据进行频率统计分析，对提取的部分评价因子进行重新赋值。

正样本原型数据频率采集统计结果：

评价因子	值域	中心值
坡向	[4.63, 5.05]	5.00
坡度	[9.09, 12.12]	10.61
剖面曲率	[3.76, 5.64]	4.70
工程地质岩组	[1.89, 2.11]	2.00
多年年均降雨	[1 279.74, 1 365.05]	1 322.39

4.1.2 滑坡负样本数据集

通过 Python 完成 K-Means、GMM、SOM 3 种聚类模型设置与数据处理。将 K-Means 类别数量设置为 5， GMM 聚类类别数量设置为 6， SOM 输入神经元节点为 8 个，其他参数保持默认设置。根据危险性分区制图的危险性等级需求将聚类分析结果划分 5 个类别，并计算各个无监督聚类模型下不同易发性等级的滑坡频率比。

根据分级图可知，滑坡极低易发区有较高的重合度，表明在提取滑坡极低易发区方面有较高的适用性。经比较统计结果，发现频率比与易发性等级的变化趋势相一致，说明GMM、SOM与K-Means 3种聚类模型能够较为准确地评价实验区滑坡易发性的空间分布情况。

对 3种模型输出结果中划分为极低易发区的数据进行提取，利用缓冲区分析剔除以滑坡正样本为中心2 km范围内的数据，将余下数据构建为采样优化的负样本数据集，降低正样本数据混入负样本数据集的可能性，保证了负样本数据的客观性与可靠性。

图4 莆田市无监督聚类易发性分级

图5 采样优化样本点空间分布情况

4.2 基于机器学习的滑坡易发性评价模型构建

基于 RF 与 SVM 模型，结合采样优化的正负样本数据集，训练构建滑坡易发性评价模型。为进一步探究本文采样优化方法获取的正负样本数据可用性，分类构建了 3种正负样本数据集用于模型训练，分别为已知滑坡样本与其缓冲区2 km范围外随机提取的样本构成原始数据集（Raw Data， RD）、筛选扩充正样本与其缓冲区2 km范围外随机提取的样本构成扩充数据集（Data Augmentation， DA）、采样优化正负样本数据集（Sample Optimization， SO）。

表6 模型超参数调优结果

模型类别	主要参数	超参数范围	RD	DA	SO
RF	n_estimators	50, 100, 150	150	100	150
	max_depth	3, 5, 10	10	10	10
	min_samples_split	5, 10, 15	5	5	5
	min_samples_leaf	5, 10, 15	5	5	5
	max_features	sqrt, log2	sqrt	sqrt	sqrt
SVM	C	0.1, 1, 10	1	1	1
	gamma	scale, auto	scale	auto	scale
	kernel	linear, rbf	rbf	rbf	rbf

表7 数据集分类准确率与模型预测精度计算结果

项目	RD-RF	DA-RF	SO-RF	RD-SVM	DA-SVM	SO-SVM
训练集准确率	0.86	0.87	0.95	0.77	0.89	0.93
测试集准确率	0.75	0.77	0.91	0.69	0.72	0.92
完整数据集准确率	0.84	0.85	0.94	0.75	0.86	0.93
最佳交叉验证得分	0.72	0.80	0.92	0.68	0.76	0.92

4.3 模型精度分析

由RD、DA构成的正负样本数据集在RF与SVM模型中，训练集与测试集之间的差异均超过0.05，表明使用RD、DA数据集构建的RF与SVM模型存在过拟合。尽管由DA数据集构建的DA-RF与DA-SVM模型所得到的最佳交叉验证得分比由RD数据集构建的模型最佳交叉验证得分有明显提高，在一定程度上改善了模型性能，但是仍低于各自的训练集得分，进一步说明未经过采样优化样本数据构建的模型泛化能力不足。

采样优化样本数据集构建的SO-RF与SO-SVM模型，在训练集和测试集上的表现均取得了较好的结果，SO-RF训练集得分（0.95）和测试集得分（0.91）之间的差异为0.04，交叉验证得分（0.92）与测试集得分较接近，表明通过采样优化方法构建的RF模型具有良好的泛化能力。SO-SVM在训练集和测试集上的表现都非常优秀，训练集得分（0.93）和测试集得分（0.92）之间的差异仅为0.01，在交叉验证方面的得分（0.92）与测试集得分一致，表明采样优化方法能够有效提升模型性能。

图6 ROC 曲线

根据ROC曲线图可知，SO-RF的AUC值为0.9756，SO-SVM的AUC值为0.9776，两者AUC值相接近，仅有0.0020的差距，说明基于采样优化方法构建的SO-RF与SO-SVM模型在易性性评价任务中均表现优秀，且具有较高的可用性，能够明显提升滑坡易发性评价模型的准确度。

4.4 滑坡易发性评价分析

基于各模型的数据集准确性及模型预测精度结果，采用SO-RF与SO-SVM对莆田市实验区进行滑坡易发性预测与分区制图，将所有栅格样本的模型预测结果作为易发性指数，并将其从高到低排序，按照1:2:4:2:1的面积比划分出滑坡极高易发区、滑坡高易发区、滑坡中等易发区、滑坡低易发区、滑坡极低易发区5个区划等级进行滑坡易发性评价研究。

图7 基于SO数据集的莆田市滑坡易发性分级图

由图7可知，SO-RF与SO-SVM模型均将实验区中部及北部划分为极高易发区，东南部均为极低易发区。实验区中部是年均降水量较高区域之一，区域内以东圳水库为中心围绕着数个村庄，同时还建设有森林公园等游览设施，人类经济活动较多，北部地形复杂，村庄周围山地海拔超过500 m，且有隧道从中穿过，频繁的交通活动可能对该区域地形地貌产生影响，滑坡致灾因素众多。滑坡极低易发性区内地势平坦，属于沿海城市带，经济水平较高，少有滑坡致灾因素。

结合实际地理环境，将中部和北部区域划分为滑坡极高易发区具备合理性，验证了应用本文提出的采样优化方法构建滑坡正负样本数据集能够提升滑坡易发性规律的解释性。因此，SO-RF比SO-SVM具有更好的适用性与合理性，更适合有限小样本滑坡数据的易发性评价。

5 结论与讨论

5.1 结论

本文开展训练样本采样优化与机器学习结合的滑坡易发性评价方法研究，融合滑坡正样本原型采样（PBS）方法与无监督聚类模型，构建了正样本数据筛选扩充与负样本数据客观提取的训练样本采样优化方法。基于采样优化方法获取的正负样本数据集，结合随机森林、支持向量机2种机器学习模型，以莆田市为实验区进行滑坡易发性评价，分析对比不同模型的准确率及模型性能，得出以下结论：

通过PBS对正样本进行数据筛选扩充，获取的正样本数据质量更高，与传统缓冲区方法相比，能够更客观的代表区域滑坡地理因素，避免了可信度较低的样本进入样本数据集。基于采样优化样本数据构建的易发性评价模型与直接使用数量较少的原始数据集构建的模型相比，评价模型最佳交叉验证得分均提高了8%以上，混淆矩阵总体准确率提高了2%，有效改善了模型性能，让模型学习训练了更多的滑坡特征，提高了在未见数据上的泛化能力。
结合无监督聚类进行负样本客观提取，能够提高负样本数据的可信度，有效解决了传统随机抽样造成的样本偏差及空间分布不均匀导致的欠采样问题，也极大程度避免了高易发性区域样本数据进入负样本数据集的过采样问题，有效提升了模型评价的准确率。SO-RF与SO-SVM模型交叉验证得分、总体准确率、ROC曲线得分分别为0.92与0.92、0.91与0.92、0.98与0.98，对比DA-RF与DA-SVM模型分别提升了0.12与0.16、0.13与0.20、0.11与0.18。研究结果表明，加入客观提取滑坡负样本的采样优化数据集比传统方法随机提取的负样本数据集具有更高的分类预测精度与准确率，验证了结合无监督聚类方法客观提取的负样本在模型评价方面更具有效性。
基于训练样本采样优化与RF、SVM结合的易发性评价模型性能、预测准确度均取得较好的表现，通过与不同数据集进行对比验证可知，由RD、DA得到的训练集准确率与测试集准确率的差距均大于0.1，存在明显的过拟合，而SO-RF、SO-SVM的训练集准确率与测试集准确率的差距分别为0.04与0.01，证明该方法能够有效缓解样本数量较少而导致模型评价结果过拟合问题。SO-RF、SO-SVM的历史滑坡与正样本在高、极高易发区域合计占比分别为49%与51%、67%与51%，正样本频率比均随着易发性等级提高而增加，说明易发性分级结果与实验区实际滑坡灾害之间具有较强的关联性，证明该方法针对类似莆田市滑坡小样本区域具有较高的可用性，为地质灾害采样方法与滑坡易发性评价相关研究提供了新思路。

5.2 讨论

由于滑坡成因复杂，影响因素众多，构建易发性评价模型时还有部分数据较难获取，所构建的评价因子指标可能并不全面，例如，现实中的滑坡发育过程并非静态，本文所选取的因子指标主要是静态数据，后续研究可加入如土地利用变化等动态因子数据，探究其对模型评价结果及精度的影响。

另外，本文在构建滑坡正样本原型数据集过程中直接将缓冲区作为滑坡多边形，在对影响范围较小的滑坡区域进行正样本原型数据提取时可能混入作为噪声的非滑坡数据，影响数据集质量，因此，可以考虑引入InSAR、深度学习图像识别或是多源数据融合等方法，优化滑坡多边形构建过程，降低正样本提取过程中混入噪声数据的可能性。

研究中仅使用了2种机器学习模型，由于不同模型对不同数据量与数据空间分布特征的适应性不同，未来可以尝试使用或者组合更多机器学习模型进行易发性分析，探究不同算法之间的易发性评价结果的空间差异性以及与实际滑坡灾害的关联性，以此增强滑坡易发性评价模型的泛化能力。

研究创新点

正样本原型采样方法

通过PBS方法对正样本进行筛选扩充，提高了正样本数据质量，更客观地代表区域滑坡地理因素特征。

无监督聚类负样本提取

结合K-Means、GMM、SOM三种无监督聚类模型对负样本进行客观提取，有效解决了传统随机抽样的样本偏差问题。

小样本区域适用性

提出的方法特别适用于滑坡样本数据较少的区域，有效缓解了模型过拟合问题，提高了预测准确性。

多模型比较分析

通过对比分析不同数据集和不同机器学习模型的性能，验证了采样优化方法的有效性，为滑坡易发性评价提供了新思路。