引言
地理空间数据是地理要素空间与属性特征的抽象表达,其涵盖的几何、属性、语义与空间关系等信息为地理空间综合分析提供了研究基础。随着信息技术的发展,地理空间数据的获取方式日趋成熟,但亦伴随着一些突出的基础性问题。由于不同数据源的比例尺与现势性等差异,多源地理空间数据在更新与集成过程中无法完全避免地理实体表达错误、地理要素空间冲突、拓扑关系不一致等问题。
等高线与河流作为两类基本地理要素,两者之间具有显著的空间相关性。通常,矢量空间数据生产周期相对较长,河流水位高低易受季节、气候等影响,使得河道亦随之拓宽或缩窄。由于数据采集方式、更新周期、异源数据精度及表达尺度差异等因素的影响,在空间数据集成、更新及维护过程中,这两类要素之间常出现等高线"落水"、河流偏离山谷线等空间关系不一致现象,这极大地制约了其在水库选址、库容估算、防洪减灾等经济建设和民生福祉上的应用。
研究方法
本文研究的技术路线如图1所示,主要内容包括:① 通过节点匹配与弯曲特征分析提取河流中心线与山谷特征;② 通过建立河流与山谷点、河流与山谷线的一致性规则实现等高线与双线河间的不一致性探测;③ 分别对等高线与河流进行移位变换,修正二者间的不一致区域。
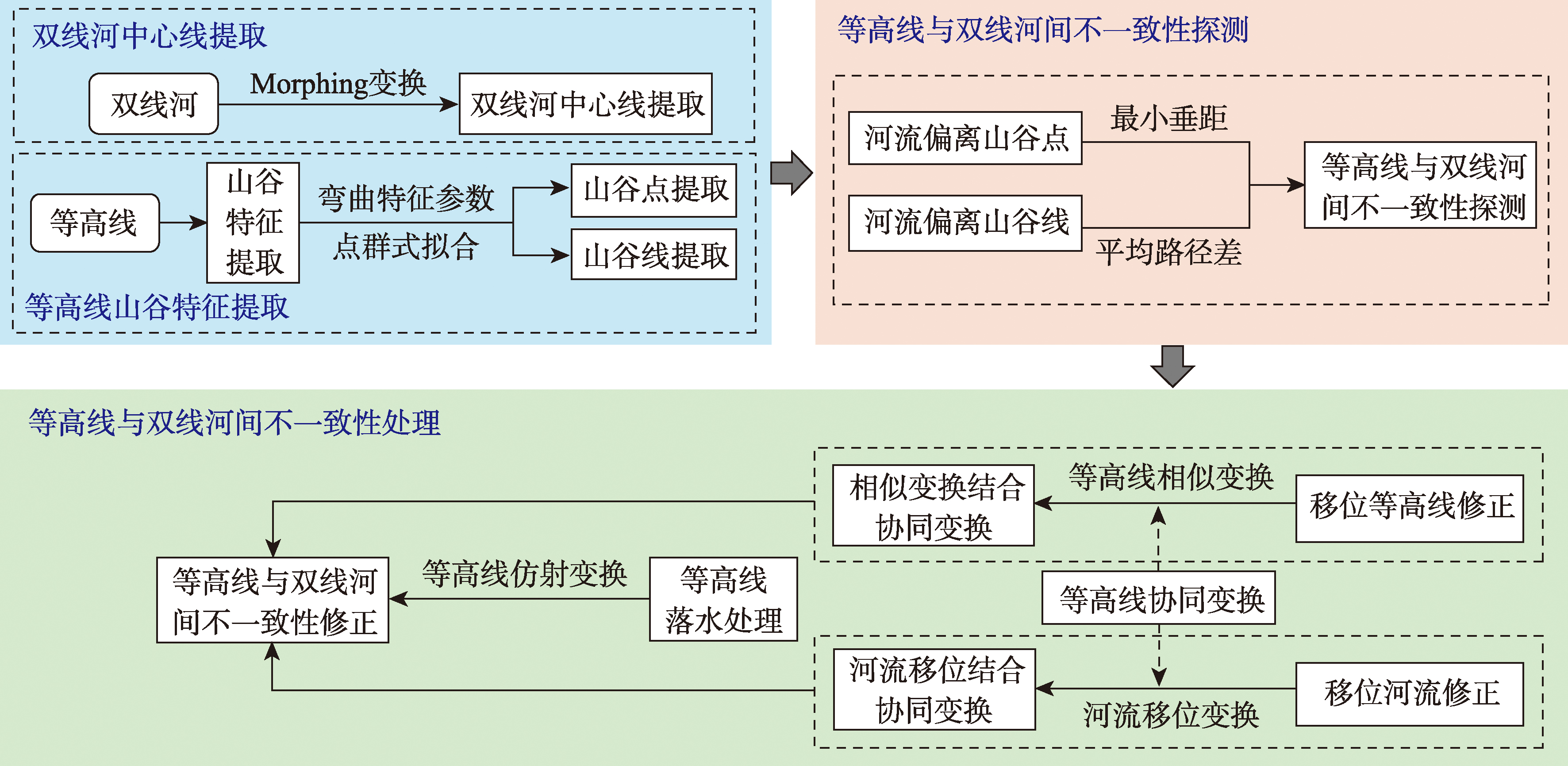
图1 等高线与双线河间不一致性探测与处理技术路线
2.1 双线河中心线提取
双线河中心线提取方法可概括为栅格类方法与矢量类方法,栅格类方法主要包括形态学细化法、中轴变换法等;矢量方法则包括非约束边中点法、Voronoi图法等。本文通过基于矢量的Morphing变换来提取双线河中心线,Morphing变换是一种图像处理技术,在不一致性处理、制图综合等领域具有广泛应用。
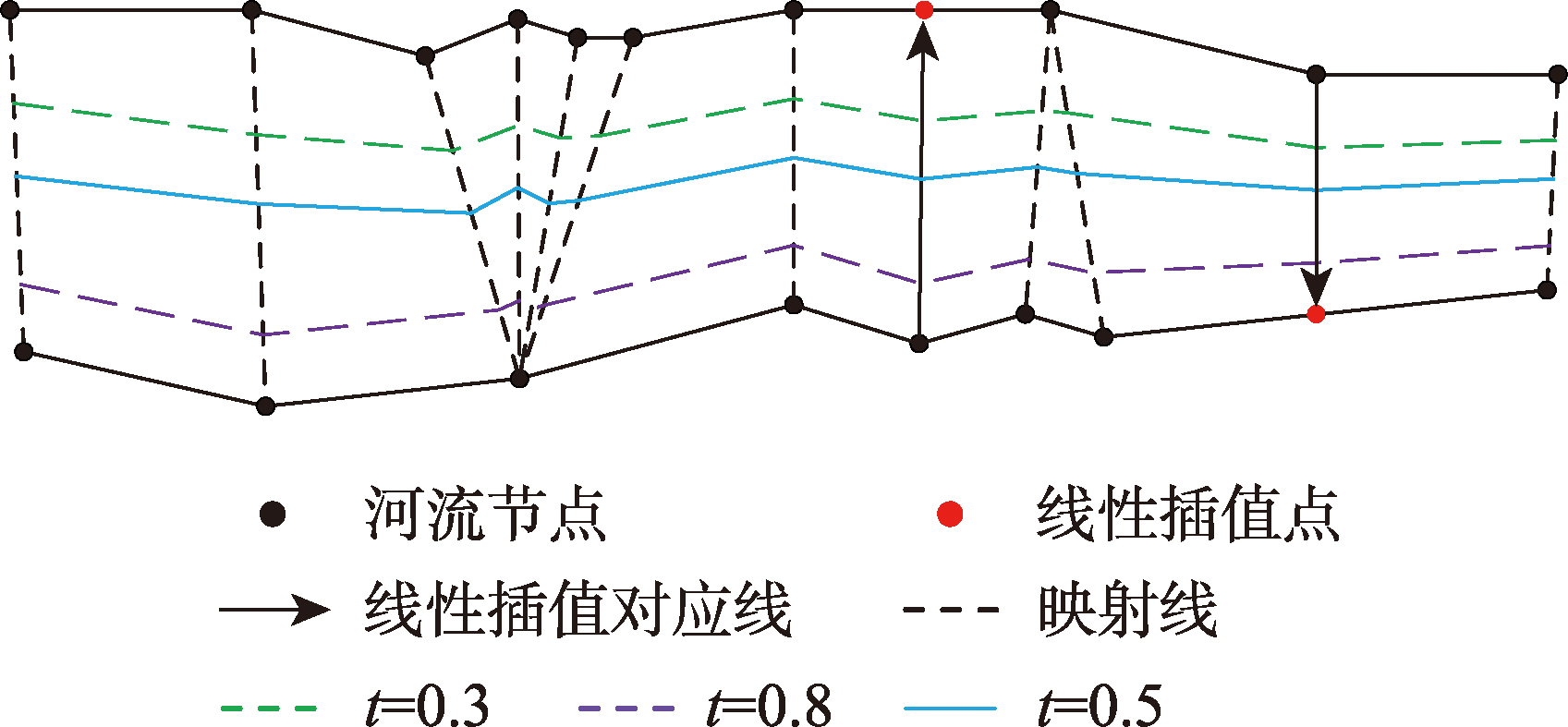
图2 双线河中心线提取
2.2 山谷特征提取
2.2.1 山谷点提取
山谷点作为等高线特征点,在几何上通常表现为局部曲率最大点,而仅通过曲率判别山谷点往往不够准确,因此,将等高线弯曲特征中各节点的曲率、转角、形状指数与欧氏距离作为综合判别指标进行筛选。
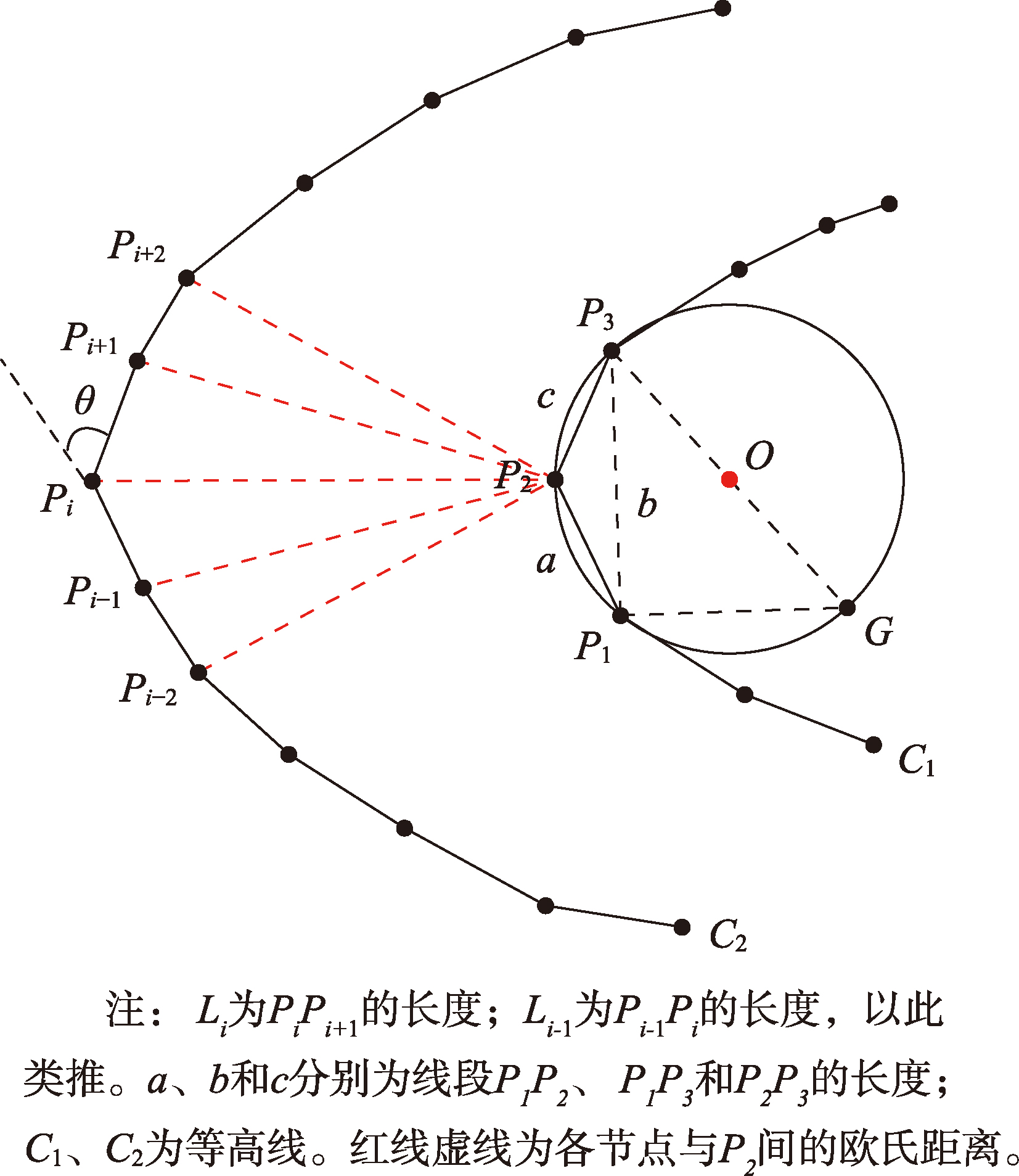
图3 山谷点特征参数计算
2.2.2 山谷线提取
从等高线提取地形特征线的方法主要有单点法与点群法2种,单点法即2条相邻等高线的特征点只通过一条直线相连,如特征点连接法,该方法较适用于一般山谷区域的山谷线提取,但在等高线形态复杂区域,则其提取的山谷线易产生多次跨越等高线等次生冲突。相较之下,点群式拟合法则能够有效减少特征线与等高线的空间冲突。
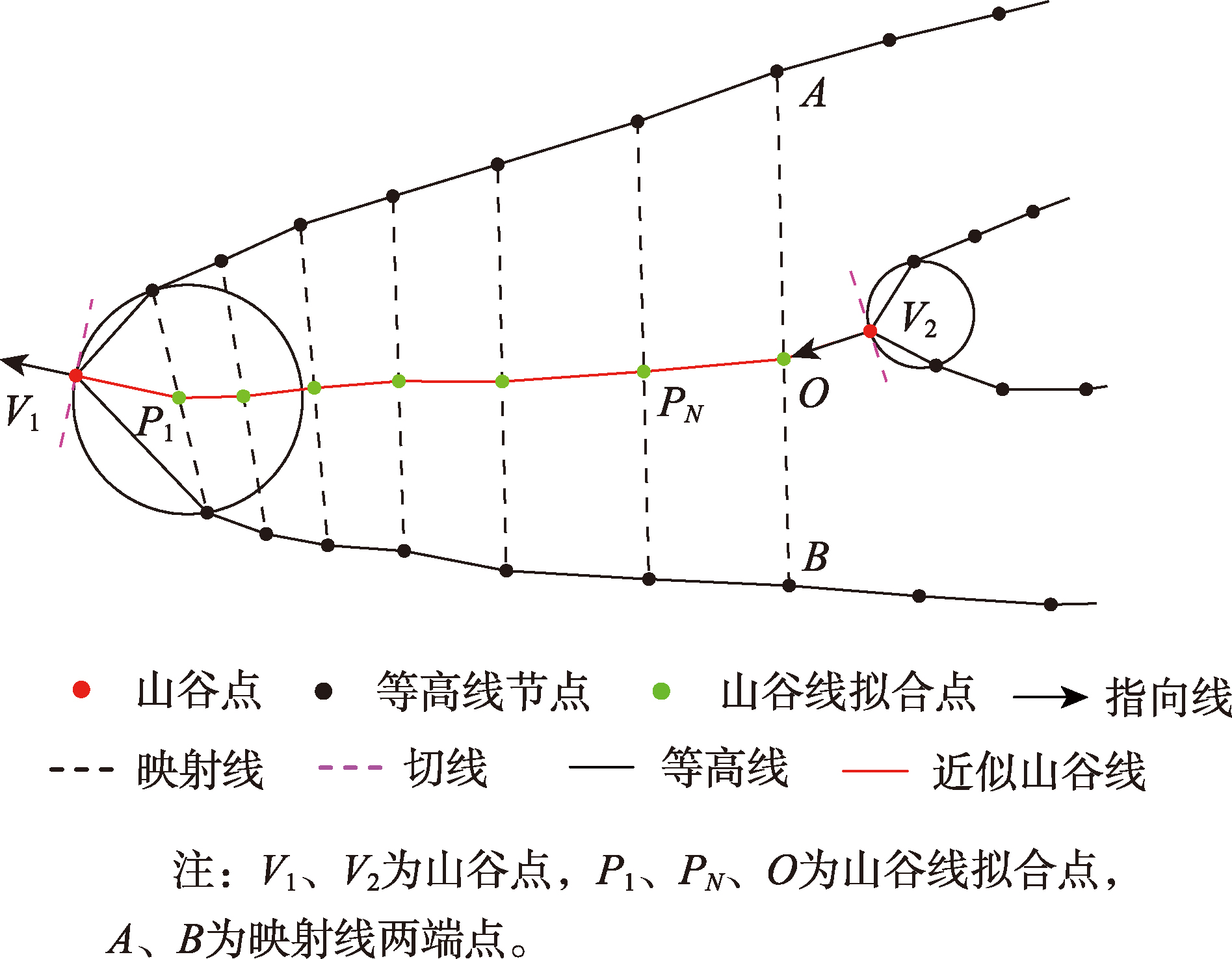
图4 山谷线提取
2.3 等高线与双线河间不一致性探测
根据地理学第一定律,同一地理表面上所有实体都是相互关联的。以等高线与河流为例,河流通过流水侵蚀改变地貌形态,导致二者间形成特定的分布模式,其几何形态体现为:① 河流与等高线的交点与山谷点重合;② 山谷线与河流重合;③ 河流流向与山谷线沿高程降低的方向一致。
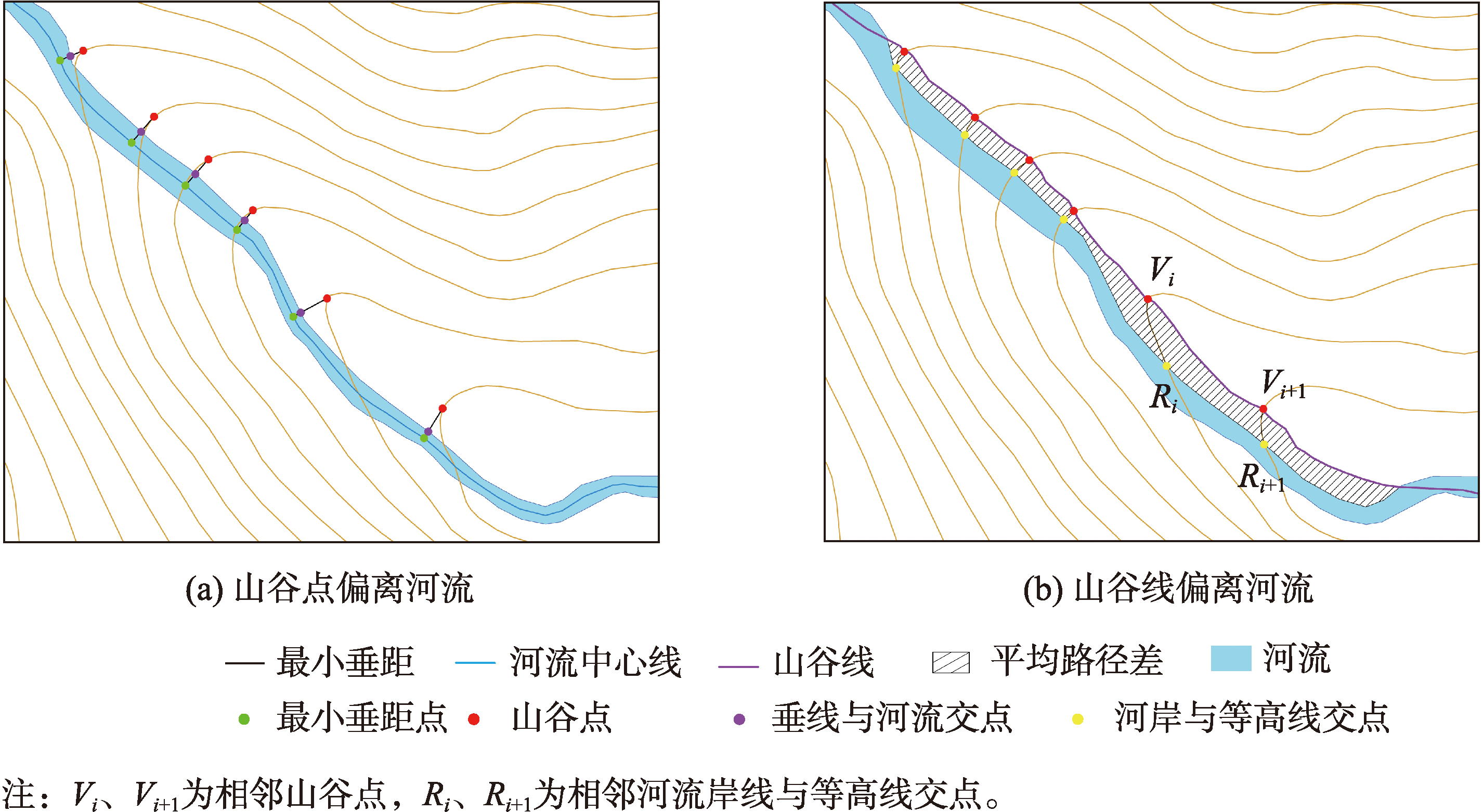
图5 等高线与双线河间不一致性探测示例
2.4 等高线与双线河间不一致性处理
2.4.1 等高线相似变换
移位等高线修正是指通过移位局部等高线,使得山谷特征与河流之间满足一致性要求。相似变换是经过坐标系的平移、缩放和旋转的复合变换得到的一种坐标变换模型,广泛应用于图像处理、坐标转换等领域。
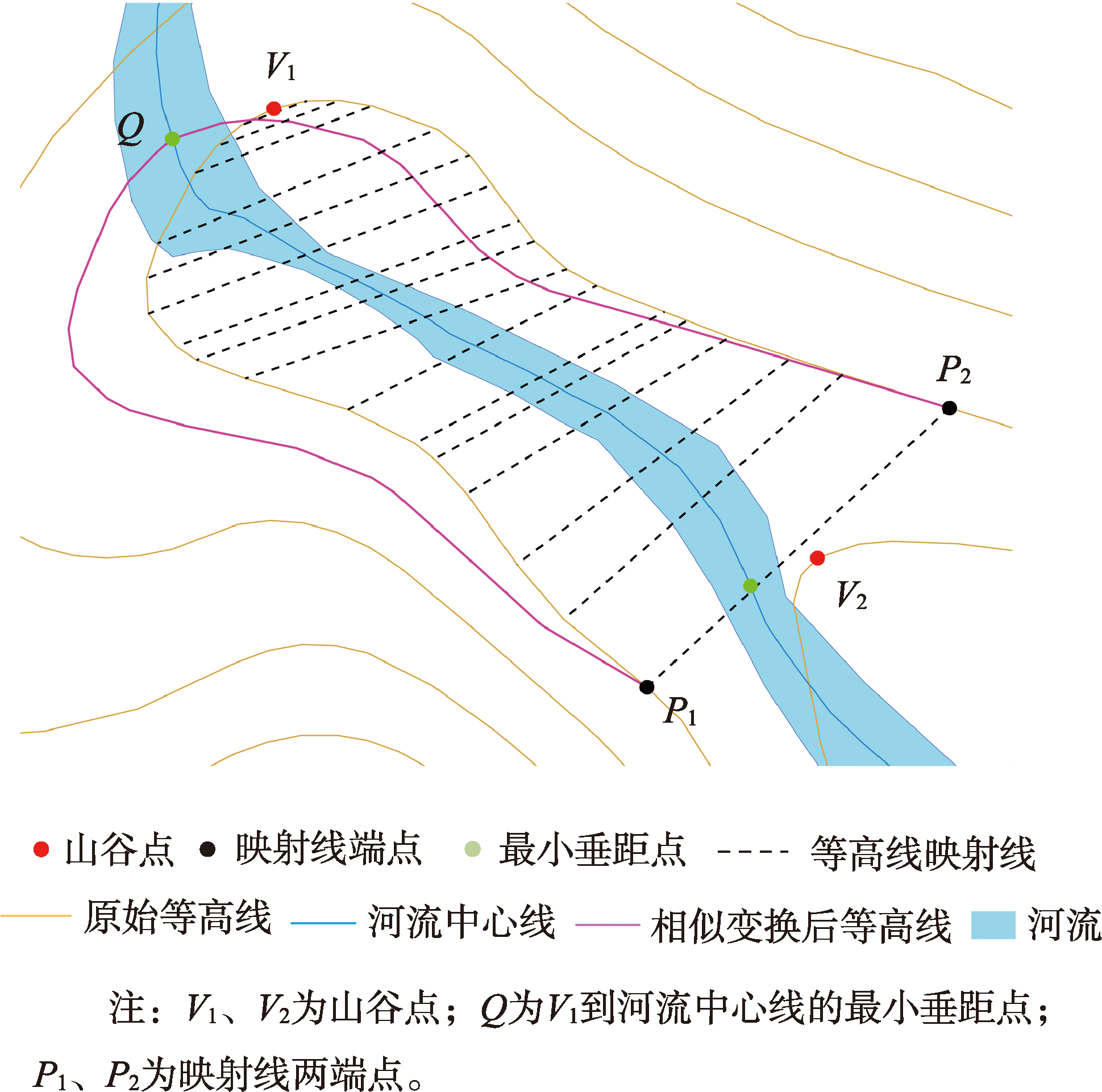
图6 相似变换修正等高线示例
2.4.2 河流移位变换
移位河流的修正方式是以河段为处理对象,需要综合考虑移位前后河流的弯曲与走势。对双线河而言,若以河流岸线与等高线的交点作为起始点,则移位后的山谷点将位于双线河岸线上,不符合等高线与双线河之间的分布模式。
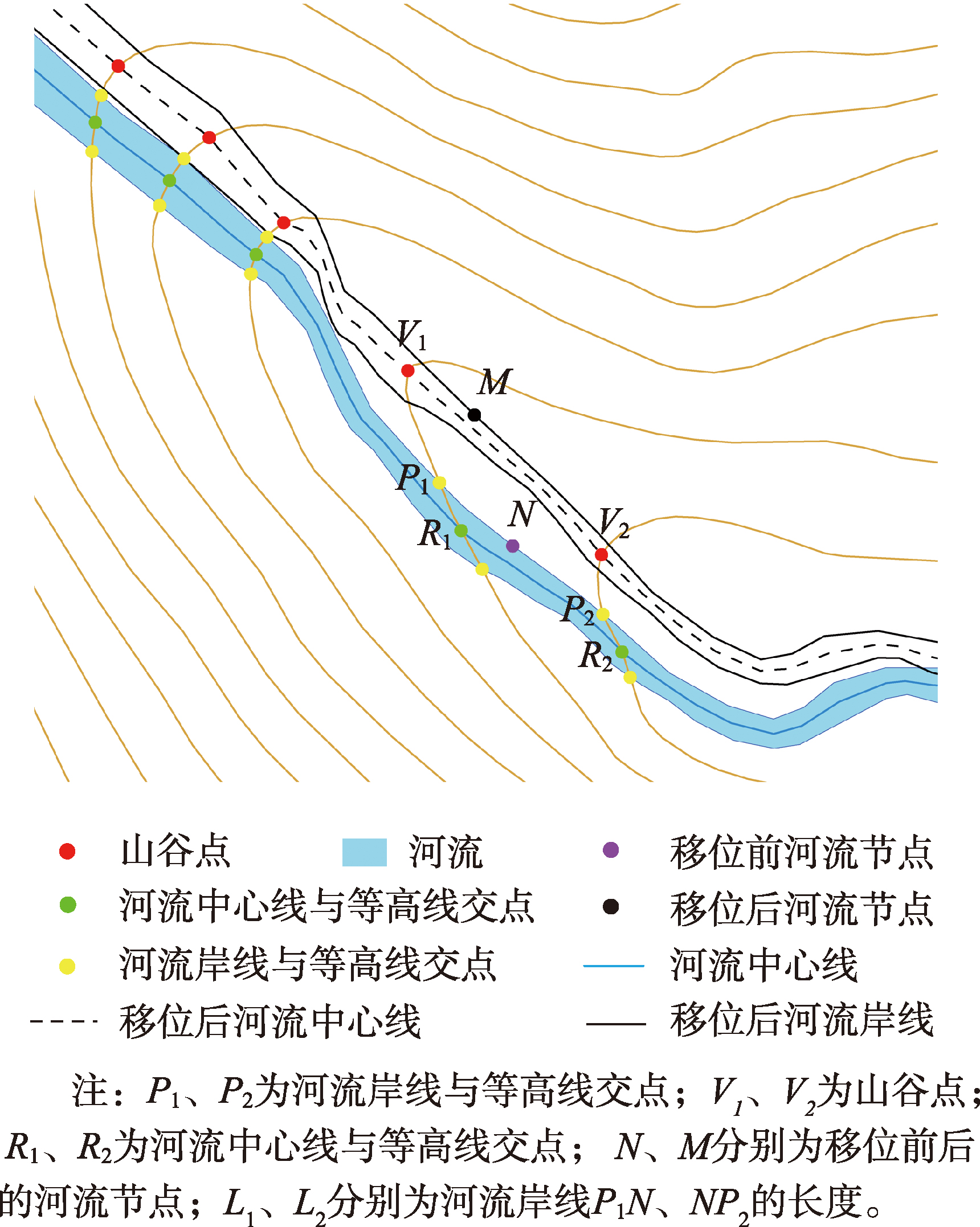
图7 移位河流修正示例
2.4.3 等高线协同变换
经等高线与河流移位变换后,山谷点均修正至河流内部,但部分区域山谷线可能与河流产生偏离,若偏差距离较大,则仍然存在山谷线偏离河流的不一致现象。本文以等高线节点间映射线为基础,通过等高线协同变换以减小山谷线与双线河之间的差异面积,使二者更契合。
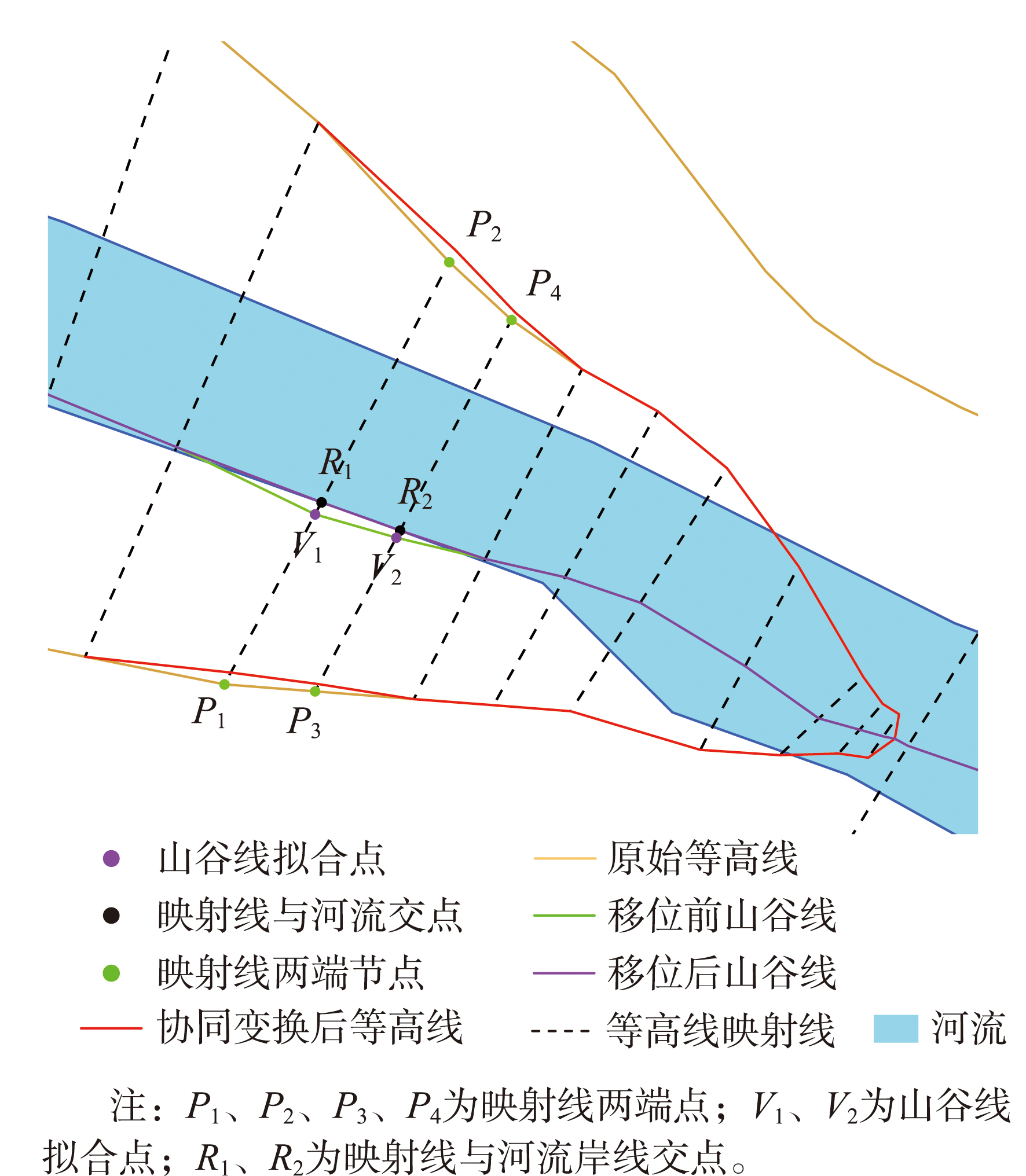
图8 等高线协同变换示例
2.4.4 等高线落水处理
由于双线河属于面状河流,等高线与双线河之间可能存在"等高线落水"的空间冲突,如图11所示,局部等高线弯曲与河流多次相交。针对该情况,本文通过仿射变换(包含缩放、平移、旋转与错切处理)进行修正。
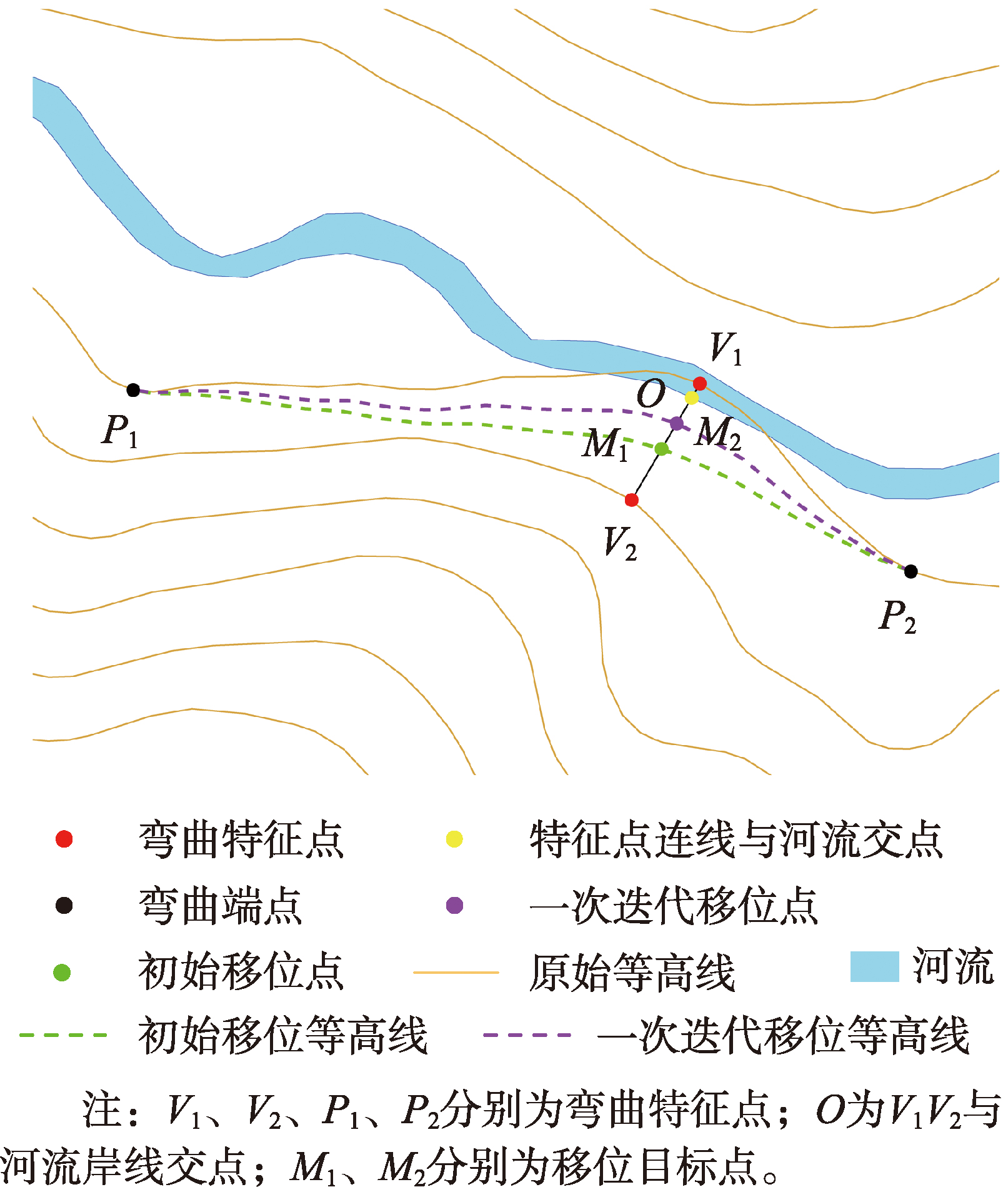
图9 等高线落水现象处理
实验与分析
本文选取云南省与安徽省共3处区域的1∶5万地形图数据进行实验,其中河流要素来源于天地图,等高线数据通过DEM生成,使用的DEM数据为ALOS PALSAR,其分辨率为12.5 m。

图10 等高线山谷特征提取与不一致性探测结果

图11 河流移位结合协同变换修正结果
表1 各区域整体平均路径差
| 处理方法 | 区域1/m | 区域2/m | 区域3/m |
|---|---|---|---|
| 修正前 | 8.323 | 8.655 | 7.126 |
| 等高线相似变换 | 5.096 | 3.059 | 6.611 |
| 河流移位变换 | 6.187 | 2.591 | 2.075 |
| 相似变换结合协同变换 | 2.417 | 0.033 | 2.783 |
| 河流移位结合协同变换 | 2.667 | 0.057 | 0.042 |
结论与讨论
4.1 结论
本文以双线河为研究对象,提出了一种等高线与双线河间的不一致性探测及处理方法,将等高线与河流间的不一致研究拓展至双线河流,得出结论如下:
- 将DTW算法融入Morphing变换以提取双线河中心线,并通过基于DTW算法的点群式拟合法提取近似山谷线,提取结果连续、平滑,符合等高线与河流的形态结构特征与整体走势,且避免了河谷处山谷线跨越等高线的问题。
- 以双线河中心线为辅助,通过最小垂距与河流岸线的空间关系检测河流偏离山谷点区域,根据LIP距离计算平均路径差来检测河流偏离山谷线区域,实现了等高线与双线河间的不一致性探测。
- 通过等高线相似变换与河流移位对不一致区域进行修正,在此基础上以映射线为枢纽,将2种方法结合等高线协同变换进一步修正后,效果更佳,在不同地形区域亦表现稳健。
4.2 讨论
本文方法以映射线为基础,充分发掘等高线与双线河的形态结构特征,对于等高线密集或稀疏区域,均有较好的适用性。以双线河中心线为枢纽进行不一致性探测及处理,亦为等高线与单线河间的不一致性分析及修正提供新的思路。对本研究的后续工作讨论如下:
- 由于河流的弯曲特性,在相邻等高线间距较大时可能存在同一等高线内河流走势变化较大现象,若河流与两侧等高线距离较近,则将与近似山谷线偏离较大。为避免位置精度的损失,本文仅探讨对于移位距离不超过50 m且移位后无次生冲突的不一致性修正问题。
- 在河流相邻节点折角处,经等高线协同变换后的山谷线与河流间可能存在极小面积差异;当等高线节点足够密集,等高线映射线与山谷线拟合点分布足够均匀时,则能进一步减小甚至消除该类区域的平均路径差,但计算工作量亦随之增加,需根据实际应用需求进行取舍。
- 除双线河外,等高线与湖泊、水库等其他面状水系要素之间的不一致性探测及处理问题还有待深入研究。