研究框架
基于菱形三十面体的矢量线球面六边形格网高精度建模方法
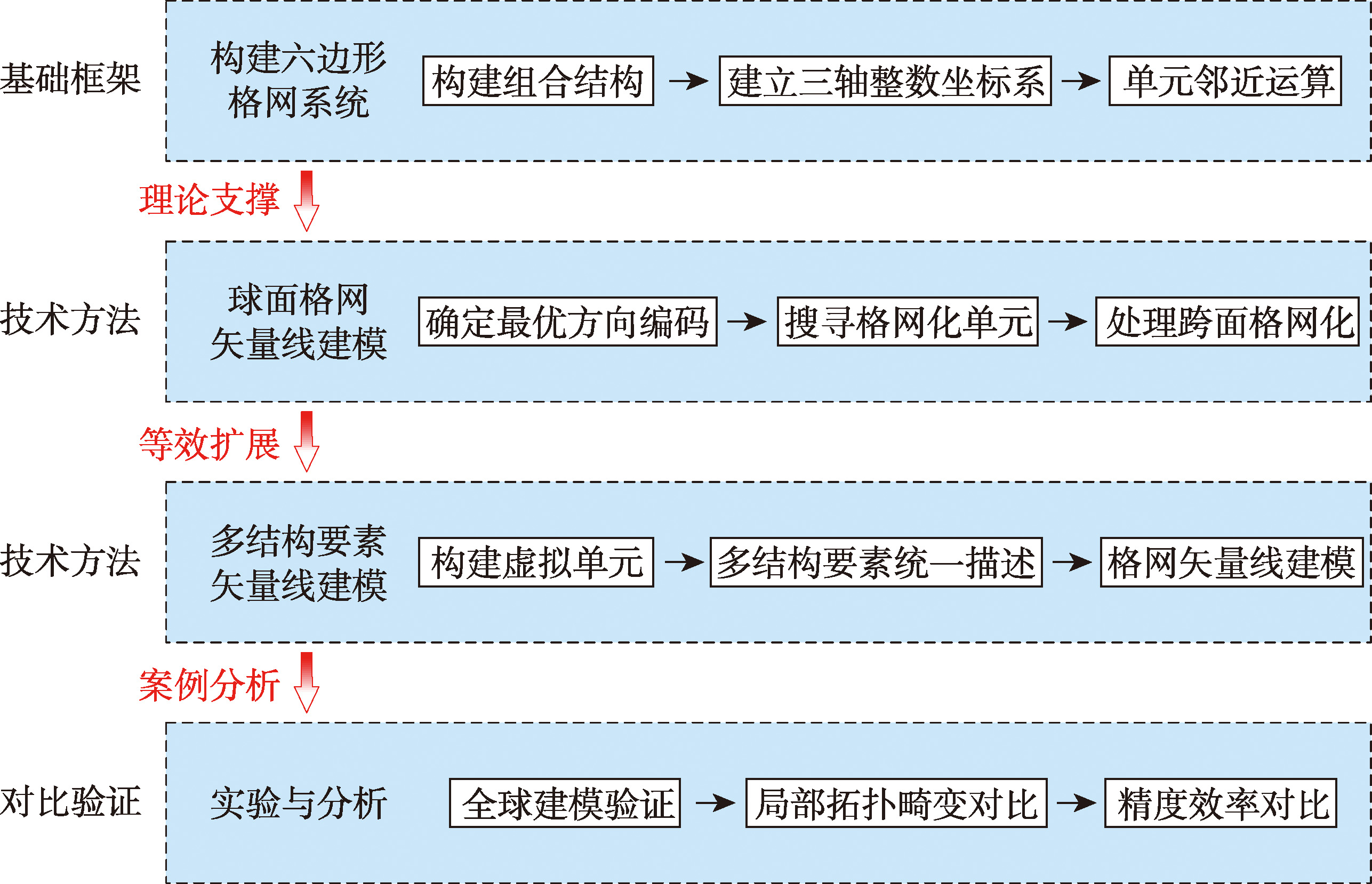
构建格网系统
选择菱形三十面体构建六边形格网,建立三轴整数坐标系
球面格网建模
确定最优方向编码,搜寻格网化单元,处理跨面矢量线
多结构要素
增加格点作为结构要素,实现多结构要素矢量线建模
验证评估
利用全球海岸线数据验证方法可行性和优越性
全球离散格网系统(DGGS)是多尺度栅格结构,地理空间矢量与格网的集成是难点
现有方案以平面格网单元中心连线为建模结果,扩展到球面后建模精度降低
矢量数据格网化过程中存在几何精度损失和拓扑畸变,影响数据质量
当矢量数据跨越多面体多个面时,容易导致矢量断裂,跨面处理是研究难点
基于菱形三十面体的矢量线球面六边形格网高精度建模方法

选择菱形三十面体构建六边形格网,建立三轴整数坐标系
确定最优方向编码,搜寻格网化单元,处理跨面矢量线
增加格点作为结构要素,实现多结构要素矢量线建模
利用全球海岸线数据验证方法可行性和优越性
构建与地球拟合程度更高的六边形格网系统
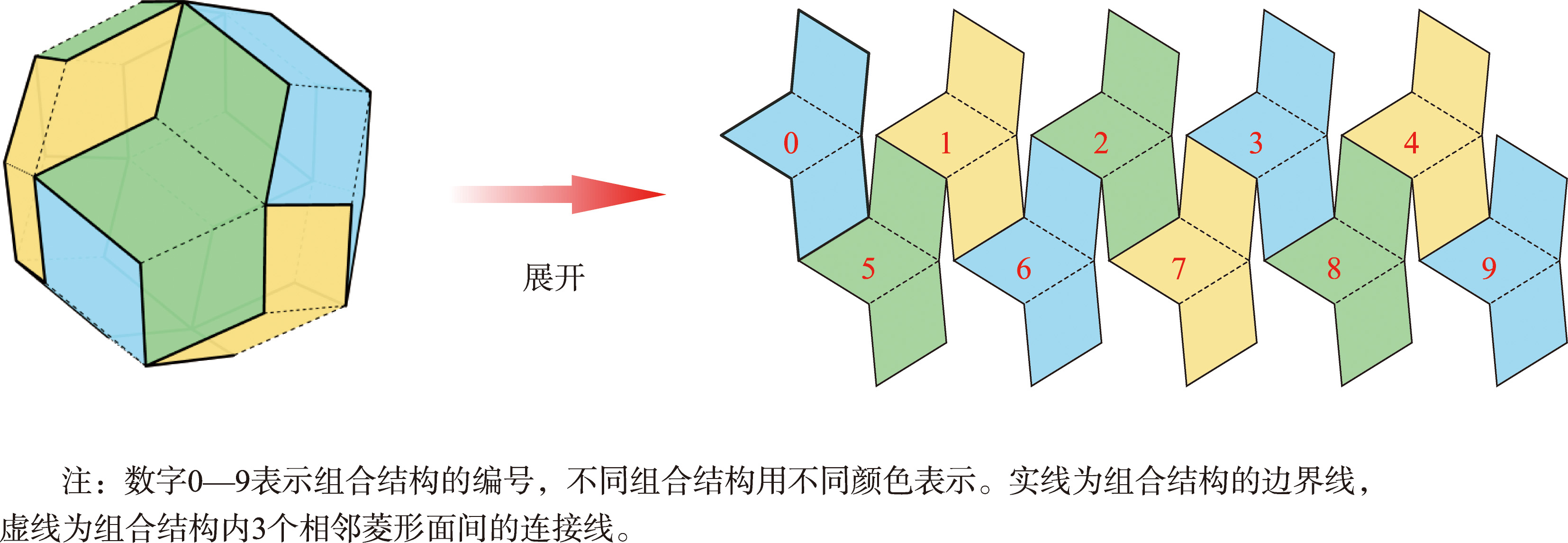
将相邻的上、中、下3个菱形面组合,菱形三十面体可由10个完全相同的"组合结构"组成
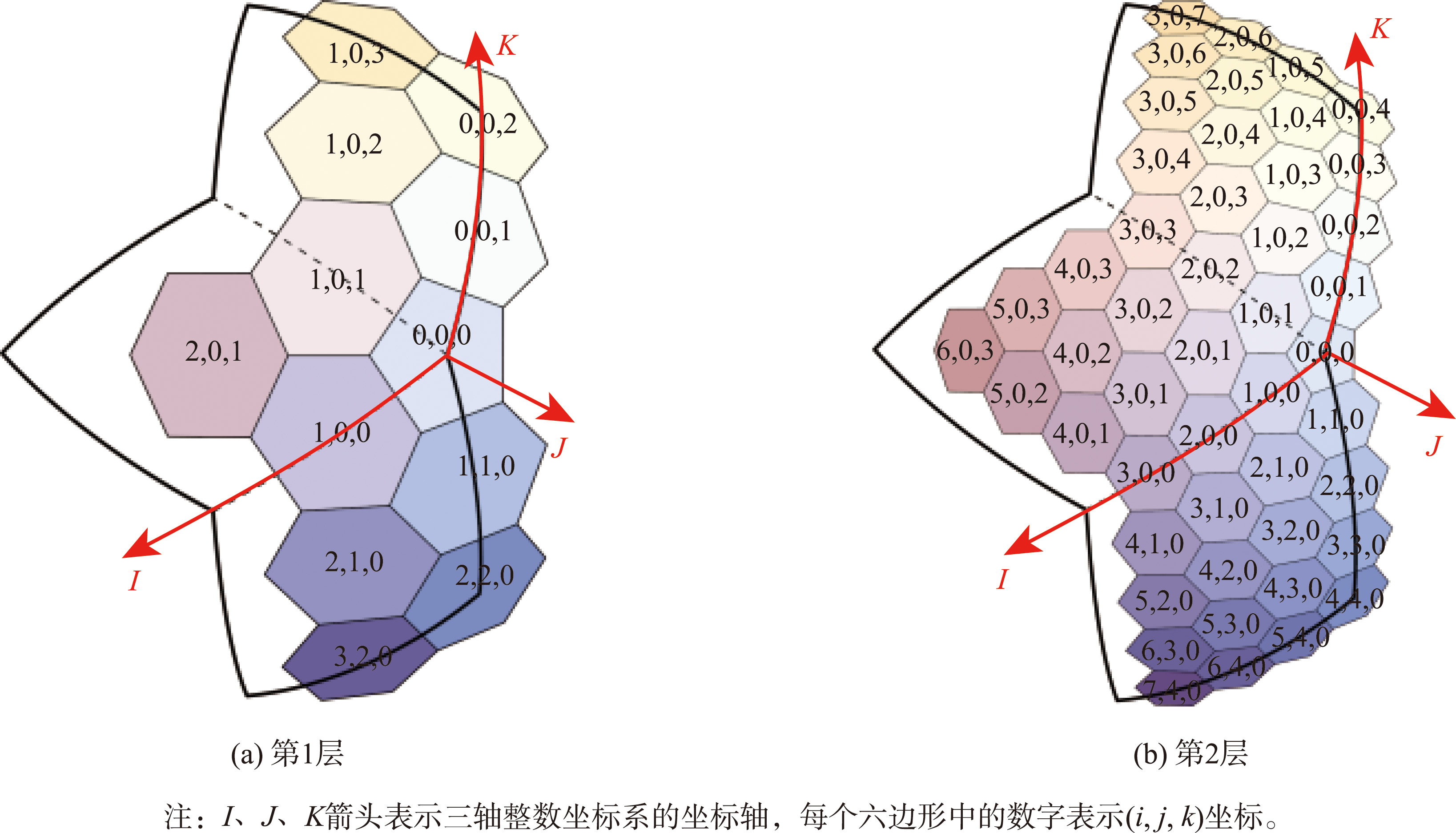
以3个菱形面的公共顶点为原点,沿着菱形面的边建立三轴整数坐标系IJK
面数更多的菱形三十面体与球面差异更小,单元变形较小
将30个菱形面的跨面运算简化为10个组合结构间的运算
同一组合结构内的单元通过简单整数坐标加减实现邻近运算
基于球面测地线的高精度矢量线格网化方法
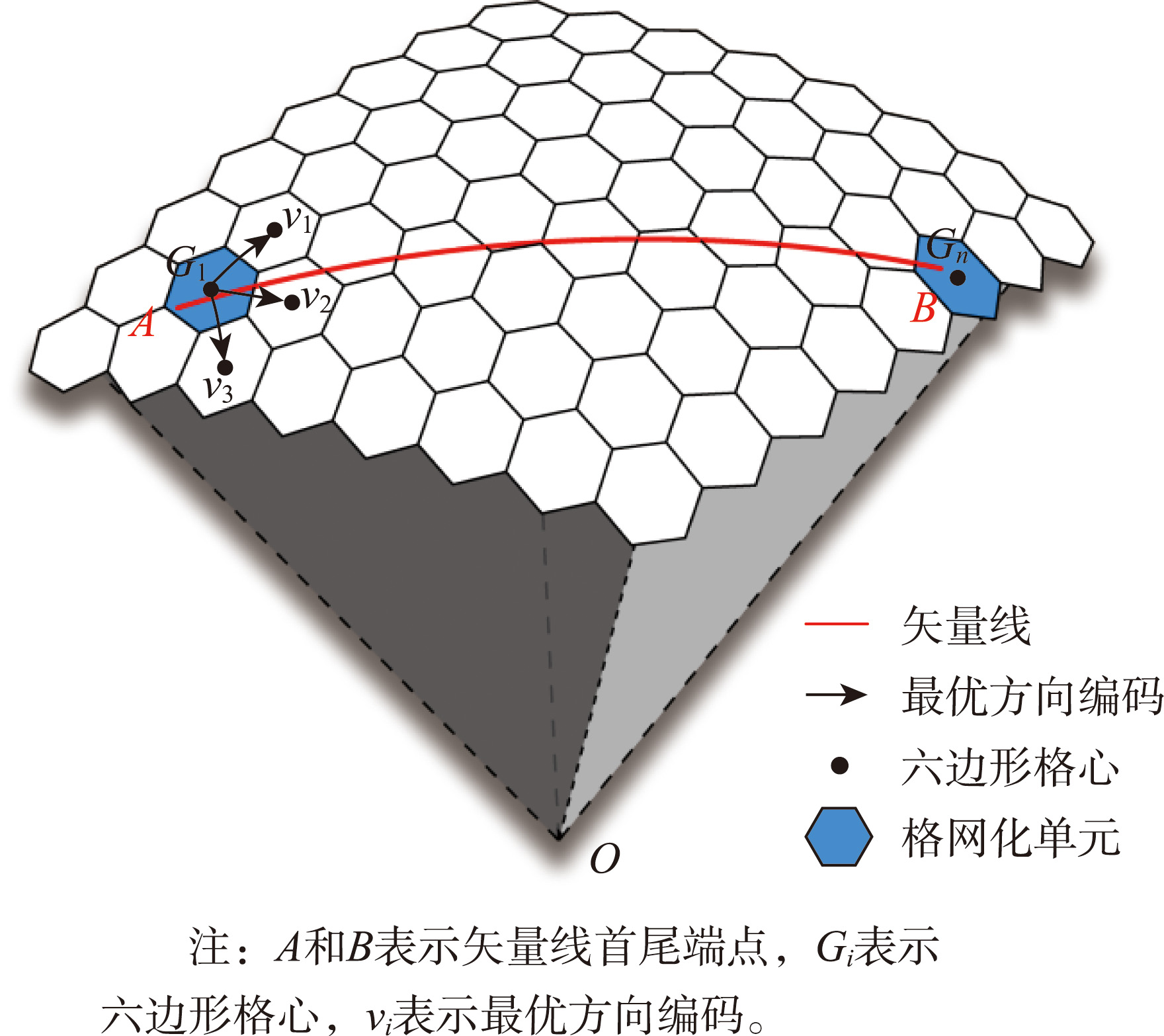
v1, v2恰好位于矢量线的两侧
v3与矢量线方向密切相关
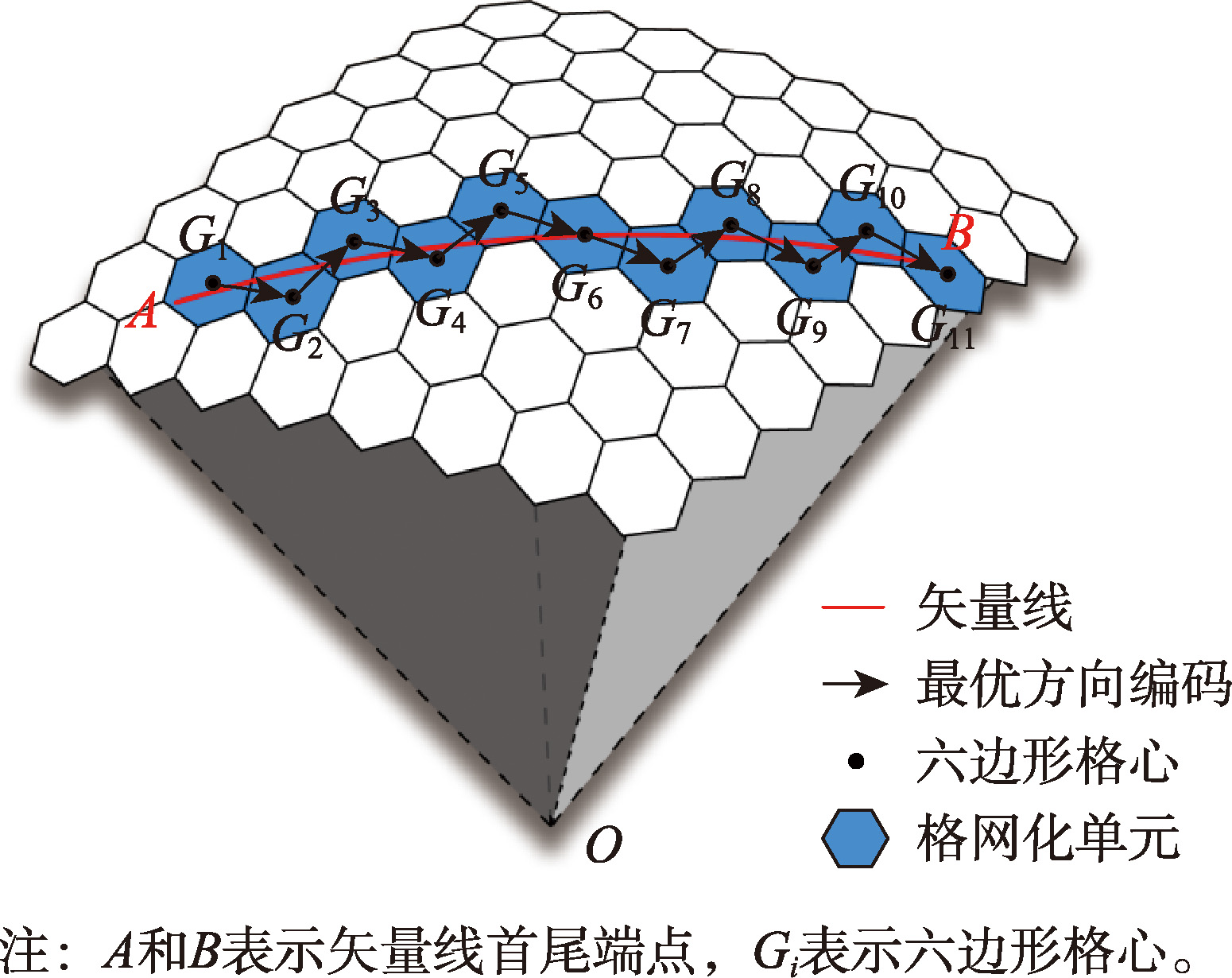
以矢量测地线为参考线,计算格心到矢量线的球面距离,选择距离最小的单元
用格心至平面OAB的距离代替球面距离,避免复杂球面三角函数计算
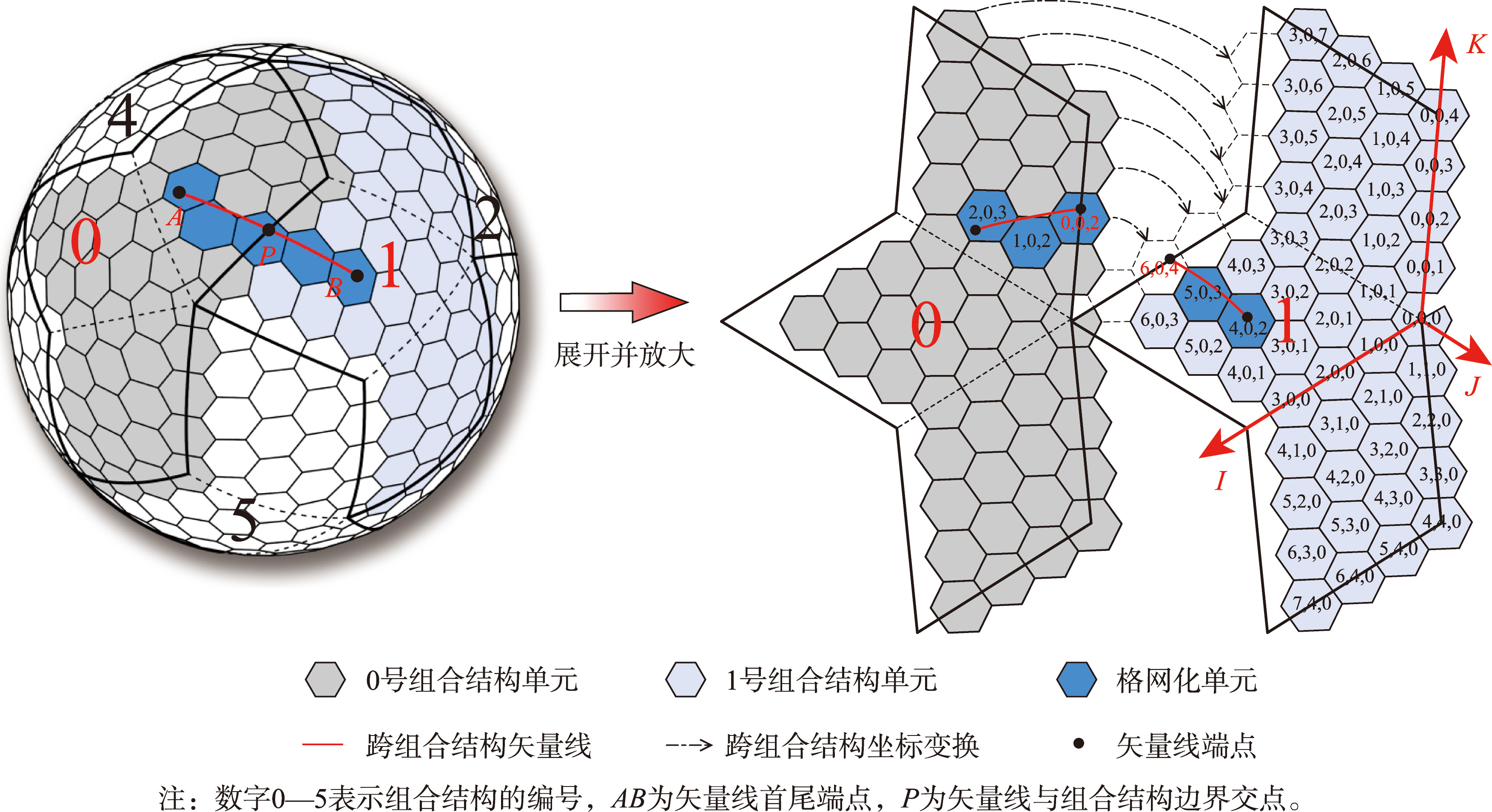
计算菱形三十面体组合结构边界与矢量线的球面交点,将跨面矢量线分解到邻近的2个组合结构中分别进行格网化
引入格点作为结构要素,进一步提高建模精度
原始单元格心对应虚拟单元坐标为(3i, 3j, 3k)
格点对应虚拟单元坐标通过整数坐标邻近查询得到
单元中心位置,传统格网化的主要结构要素
单元覆盖区域的边界点,能与位置相关数据建立关联
常用作战场环境建模时障碍类要素的辅助表示
基于全球海岸线数据的方法验证与性能评估
精度提升显著,兼具精度和效率优势
几乎不受原始矢量数据分辨率影响
即使在复杂球面几何运算后仍保持效率优势
| 判断条件 | 最邻近最优方向编码 | 第三最优方向编码 |
|---|---|---|
| di < 0, dk ≥ 0 | v1=(-1,0,0), v2=(0,0,1) | v3=(-1,0,-1) / v3=(1,0,1) |
| di ≥ 0, dk > di | v1=(0,0,1), v2=(1,0,1) | v3=(-1,0,0) / v3=(1,0,0) |
| di ≥ dk, dk > 0 | v1=(1,0,1), v2=(1,0,0) | v3=(0,0,1) / v3=(0,0,-1) |
| di > 0, dk ≤ 0 | v1=(1,0,0), v2=(0,0,-1) | v3=(1,0,1) / v3=(-1,0,-1) |
与传统平面格网建模方法的全面对比分析
相比平面格网建模,几何精度显著提升,有效减少精度损失
确保格网化单元与矢量线拓扑相交,避免拓扑畸变问题
通过编码邻近运算简化搜索过程,保持高效的计算性能
为矢量数据转换至格网同构处理提供有力支撑
"实验结果表明,本文方案能正确实现全球各个大洲海岸线格网化建模,确保格网化单元与矢量线拓扑相交,且相较平面格网建模结果兼具精度和效率优势。"
突破传统格网建模方法的技术瓶颈
以矢量测地线为参考线搜寻球面格网化单元,从原理上解决偏移误差问题
采用3个最优方向编码约束球面单元搜索方向,避免搜索路径不收敛
通过求解多面体边界与矢量线交点,实现跨组合结构的无缝处理