MMTC算法：基于地图匹配和两阶段聚类的轨迹异常检测

研究背景与挑战

探索轨迹数据挖掘领域的前沿问题与技术突破

现有方法的局限性

忽略道路网络约束

传统方法仅依赖几何距离或速度变化，未充分考虑实际道路结构与通行规则

计算复杂度高

面对大规模城市轨迹数据时，大部分算法计算复杂度较高，实时性不足

误判率较高

复杂交通环境中，常出现合理绕行被误判为异常的情况，影响检测实用性

轨迹异常检测算法框架

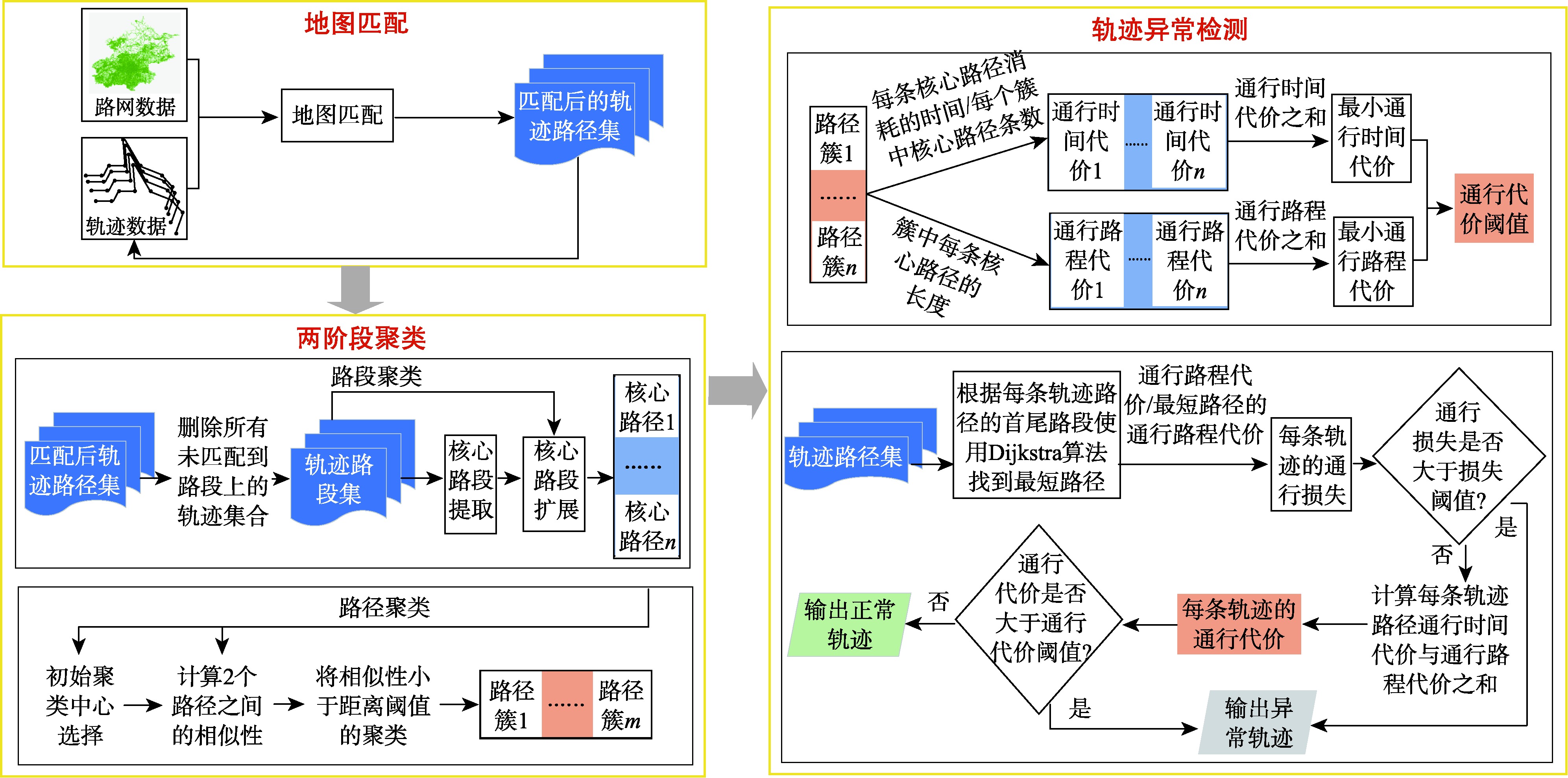
核心技术创新

MMTC算法的三大技术突破与创新优势

地图匹配技术

通过精准的地图匹配算法，将GPS轨迹数据映射至实际道路网络，生成符合真实道路布局的路径序列

距离计算公式

SD(p_jⁱ, r) = {
  D(p_jⁱ, l_i)     k ≤ 0
  D(p_jⁱ, t)       0 < k < 1
  D(p_jⁱ, l_j)     k ≥ 1
}

• 候选路段智能筛选
• 最优路段精确匹配
• Dijkstra算法路径补全

两阶段聚类

创新性的两阶段聚类策略，先基于路段密度提取核心路径，再按几何-拓扑相似性生成高质量路径簇

路段特征因子

f(r) = w₁ × d + w₂ × c + w₃ × a

d = DenV(r_t) / Σ DenV(r_i)
c = RSC(r, r_t) / DenV(r)
a = (π - σ(r, r_t)) / π

• 密度驱动核心路径提取
• 相似性度量路径合并
• 多尺度路径簇生成

异常检测判定

结合通行时间与路程代价的多维度评估体系，通过智能阈值比较实现精准异常轨迹识别

通行代价计算

CostT = Q₁ × timeCost + Q₂ × routeT

RouteLoss = routeT / LossR

异常判定: RouteLoss > LossThreshold
或 CostT > e × CostThreshold

• 时间-路程代价综合评估
• 最短路径偏离度分析
• 双重阈值异常判定

数学模型与核心定义

算法的理论基础与数学建模

轨迹与路网定义

轨迹定义

Tr_i = {p₁ⁱ, p₂ⁱ, p₃ⁱ, ..., p_jⁱ, ..., p_{len_i}ⁱ}

其中: p_jⁱ = ⟨lon_jⁱ, lat_jⁱ, time_jⁱ⟩

路网图定义

G = (V, E)

V = {l₁, l₂, l₃, ..., l_m}
E = {(eid, l_i, l_j) | l_i, l_j ∈ V}

两点距离计算

D(p₁, p₂) = R × arccos(cos(lat₁)cos(lat₂)cos(lon₁ - lon₂)
+ sin(lat₁)sin(lat₂))

其中: R = 6371 km (地球半径)

相似性与代价模型

路径相似性

Sim(Path₁, Path₂) = S₁ + S₂ + S₃

基于路径间形成的封闭多边形面积计算
S = ½|Σ_i=1ⁿ(x_iy_i+1 - x_i+1y_i)|

通行时间与路程代价

Tdist(Tr_i) = time_{len_i}ⁱ - time₁ⁱ

Rdist(Tr_i) = D(p₁ⁱ, p₂ⁱ) + ... + D(p_{len_i-1}ⁱ, p_{len_i}ⁱ)

通行代价阈值

CostThreshold = w₁ × minTimeCost + w₂ × minRouteCost

异常条件: CostT > e × CostThreshold

实验数据集与环境

基于北京市真实出租车轨迹数据的大规模验证

数据集详细信息

路网数据

2016年北京市全路网数据，覆盖超10万路段与8万节点，双向通行扩展后总路段达18万

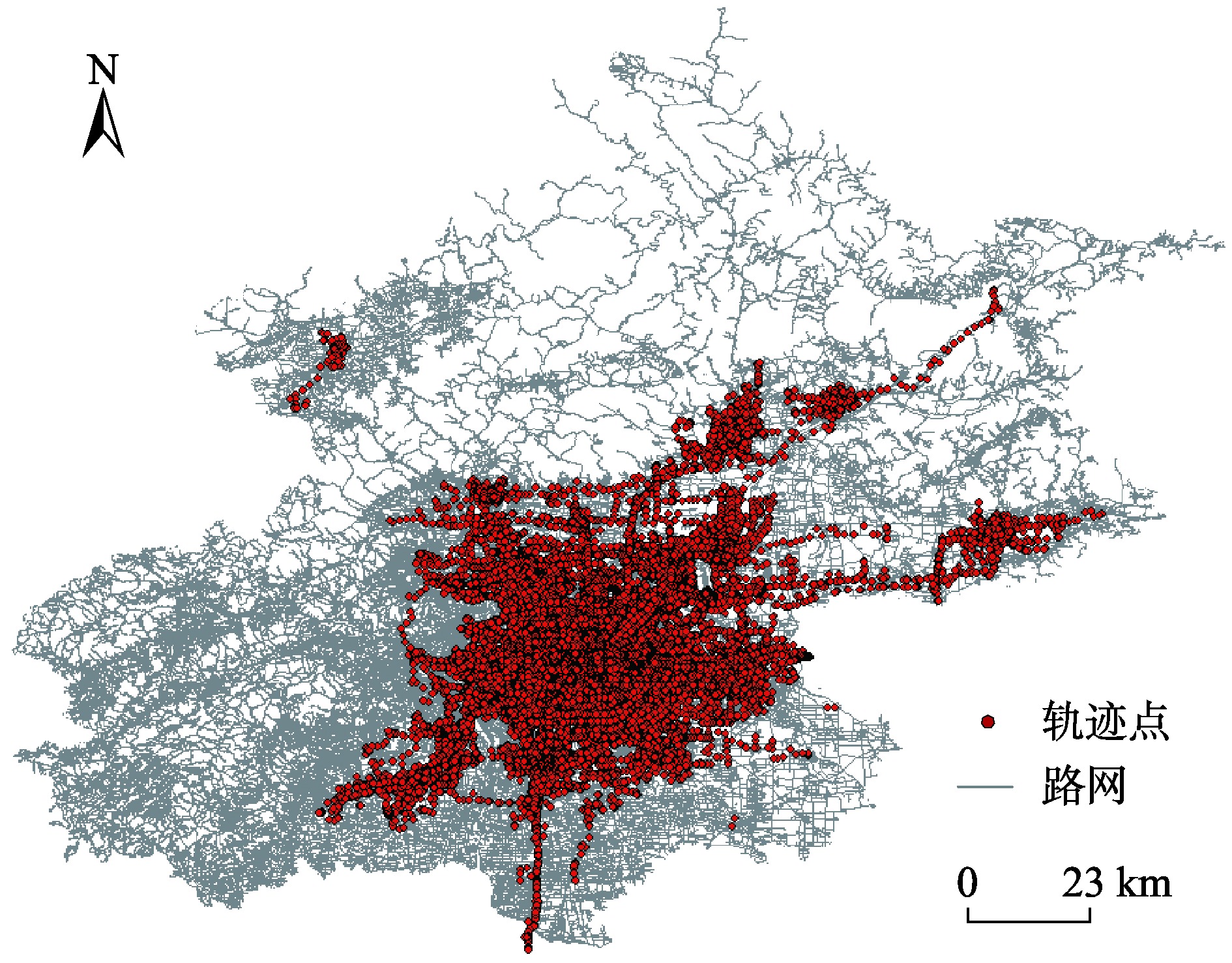
轨迹数据

2017年3月1日早高峰(8:00-9:00)采集的1万辆出租车GPS数据，平均采样间隔1分钟

数据特征

平均距离间隔658m，时间间隔60s，通过方位角聚类划分为4个子集进行验证

轨迹数据集统计信息

数据集	轨迹总数	正常轨迹	异常轨迹	异常比例
T1	2,620	1,872	748	28.5%
T2	2,008	1,417	591	29.4%
T3	2,796	2,005	791	28.3%
T4	2,463	1,647	816	33.1%

性能评估与对比分析

MMTC算法相较于传统方法的显著性能提升

核心性能指标

9.03%

准确率提升

相比STADCS算法

9.45%

F1分数提升

相比ATDC算法

6.67%

F1分数提升

相比Two Phase算法

显著

运行时间

效率大幅提升

详细性能对比

算法	准确率	精确率	召回率	F1分数
MMTC	0.880	0.897	0.930	0.918
STADCS	0.790	0.812	0.856	0.834
Two Phase	0.823	0.845	0.878	0.851
ATDC	0.798	0.821	0.834	0.823

运行时间对比

MMTC算法 28.47s

Two Phase 45.23s

ATDC 67.89s

STADCS 112.56s

轨迹异常检测可视化

真实场景下的异常轨迹识别效果展示

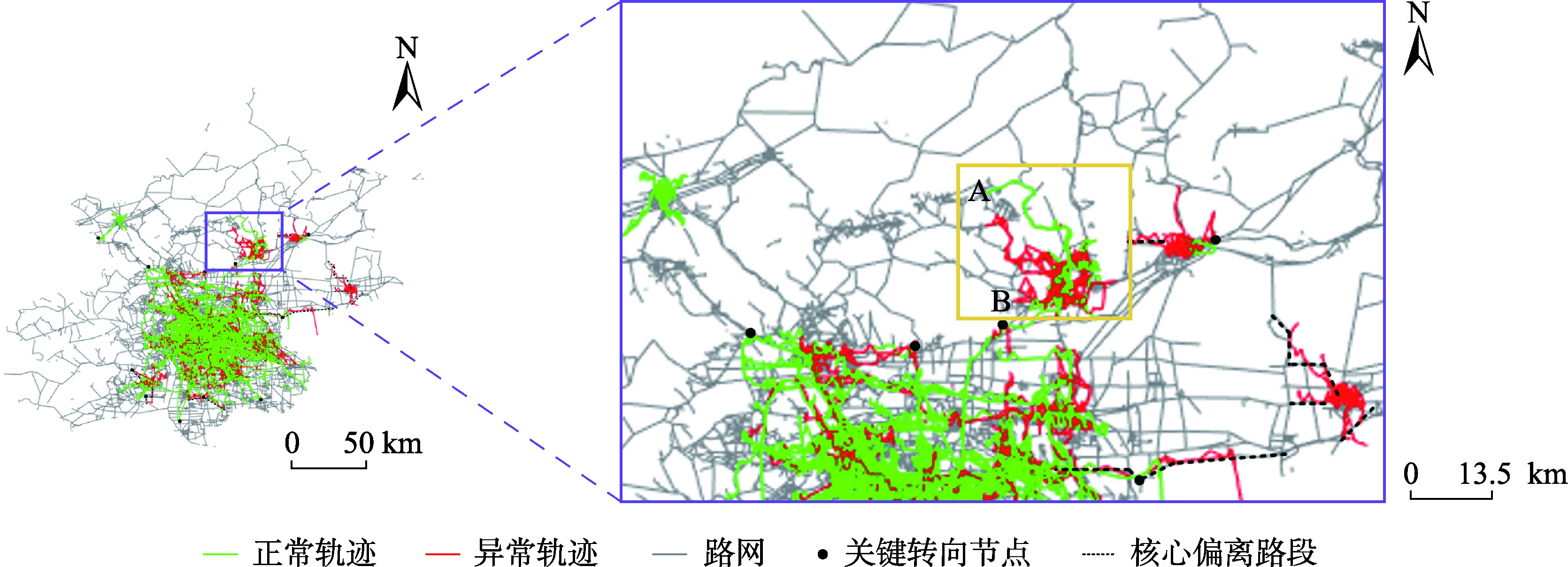
检测结果分析

正常轨迹特征

• 与最短路径高度重合
• 在主干道密集分布
• 转向规律性强
• 通行代价在合理范围内

异常轨迹特征

• 明显偏离最短路径
• 在支路频繁无意义迂回
• 连续多段路径异常
• 通行代价显著超标

关键发现

通过对北京市核心区域的轨迹分析发现，异常轨迹主要集中在交通枢纽附近，表现为明显的绕行模式。MMTC算法能够精准识别这些偏离正常路径的行为，同时有效区分合理的交通避让与恶意的欺诈绕行，为智慧交通管理提供了可靠的技术支撑。

应用价值与发展前景

MMTC算法在智慧交通领域的广阔应用前景

出租车监管

精准识别出租车司机的欺诈绕行行为，保护乘客权益，提升出租车行业服务质量和诚信水平。

• 实时欺诈行为检测
• 司机信用评级系统
• 乘客权益保护
• 行业监管支持

交通管理

为城市交通管理部门提供数据支撑，优化交通流量分配，提升道路使用效率和交通安全水平。

• 交通流量优化
• 拥堵预警系统
• 路网规划支持
• 智能信号控制

数据挖掘

深度挖掘车辆轨迹数据价值，为城市规划、商业分析、物流优化等领域提供智能化解决方案。

• 出行模式分析
• 商圈热力图
• 物流路径优化
• 城市规划支持

算法局限性与改进方向

持续优化与技术发展的未来路径

当前局限性

稀疏数据适应性

对低采样频率GPS场景适应性不足，轨迹点间隔过大时地图匹配精度下降，簇内平均相似度降低约8.13%

实时处理效率

大规模实时处理场景中，Dijkstra最短路径计算和两阶段聚类过程仍可能成为性能瓶颈

时间维度建模

仅考虑通行时间和速度代价，忽略轨迹停留时间变化，对复杂时间模式识别不足

改进方向

时空插值技术

引入历史轨迹模式挖掘和路网拓扑约束，推断缺失轨迹点位置，融合多源异构数据提升稀疏场景适应能力

并行计算优化

探索近似算法简化计算过程，采用并行计算技术充分利用多核处理器，满足交通流量实时监测需求

多维特征融合

对停留时间建模，结合驾驶行为特征进行联合分析，探索跨领域迁移能力验证算法普适性

技术创新总结

MMTC算法的核心贡献与技术突破

路网约束融合

首次深度融合道路网络结构与约束信息，通过地图匹配技术实现轨迹与实际路网的精准映射，显著提升异常检测的准确性和实用性

两阶段聚类创新

创新性的两阶段聚类策略，先基于路段密度提取核心路径，再按相似性生成路径簇，有效降低计算复杂度并提升聚类质量

多维异常判据

结合通行时间与路程代价的综合评估体系，通过双重阈值机制精准区分合理绕行与异常轨迹，大幅降低误判率

算法核心优势

性能提升

• 准确率相比STADCS提升9.03%
• F1分数相比ATDC提升9.45%
• 运行时间显著优于传统方法
• 参数鲁棒性强，适应性广

实用价值

• 适用于复杂城市路网场景
• 支持大规模轨迹数据处理
• 为交通管理决策提供支撑
• 在欺诈检测领域具有重要应用价值

以上内容由AI自动生成，内容仅供参考。对于因使用本网站以上内容产生的相关后果，本网站不承担任何商业和法律责任。