研究概览
研究目标
解决现有DEM综合方法中地貌特征保持不完整和部分地形要素过度综合的问题
核心方法
结合平面曲率和小波变换,重点突出局部地形几何特征,提升多尺度地形分析准确性
性能提升
与结构化综合方法相比,MAE和RMSE分别降低了13%和34%
技术路线
平面曲率计算
计算DEM数据的平面曲率,生成平面曲率图,突出局部地形几何特征
小波分解函数选择
分析地形地貌特征,选择双正交小波函数"bior3.9",采用对数函数确定分解层数
小波分解
对平面曲率图进行小波分解,获得对应的低频系数和高频系数
特征点选取
基于低频系数选取特征点,引入方根模型制定选取规则
空间插值
以选取的特征点为基础进行克里金插值,生成新的低频系数
小波重构
将插值结果与高频系数结合,通过高程映射得到综合后的DEM图像
核心公式
平面曲率计算
其中K为平面曲率值,fx、fy为水平和垂直方向变化率
方根模型
将综合前后地物数量与比例尺分母的方根相关联
实验结果
实验数据
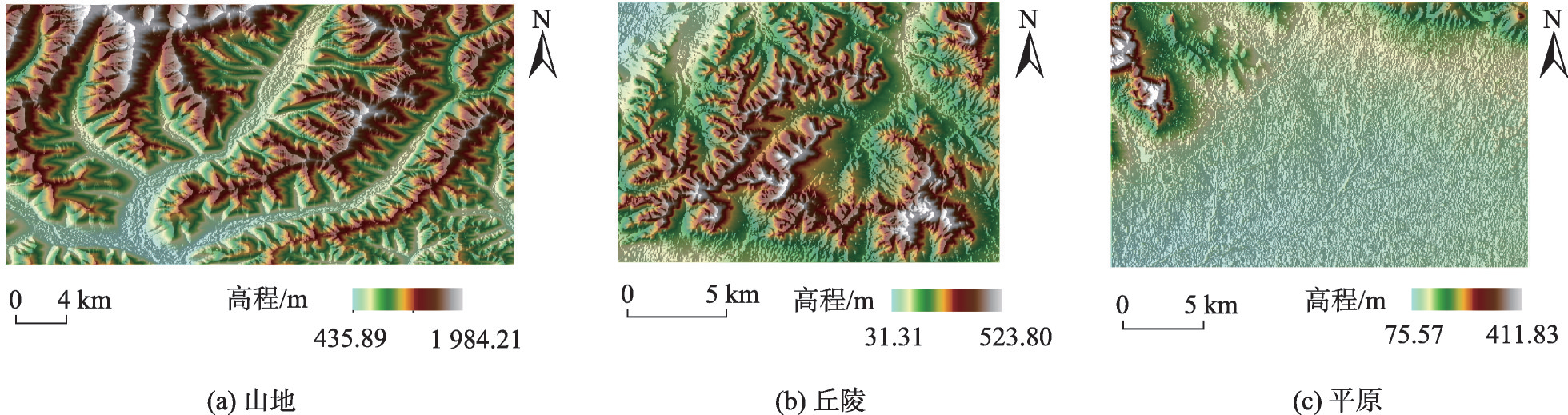
山地DEM
东北某地区
高程:435-1985m
678×1322像素
丘陵DEM
山东某地
高程:31-524m
446×654像素
平原DEM
山东某地
高程:75-412m
516×817像素
插值方法对比结果
| 插值方法 | 高程值均值 (m) | 高程值标准差 (m) |
|---|---|---|
| 原始DEM数据 | 952.245 8 | 282.004 7 |
| IDW插值 | 992.559 8 | 116.912 3 |
| 样条插值 | 950.986 1 | 282.918 4 |
| 克里金插值 ✓ | 949.207 9 | 288.302 2 |
| 自然邻点插值 | 949.147 7 | 296.511 8 |
精度对比分析
| 评价指标 | 本文方法 | 结构化综合方法 | 改进幅度 |
|---|---|---|---|
| MAE (m) | 17.976 0 | 20.668 2 | ↓ 13% |
| RMSE (m) | 29.504 8 | 44.756 2 | ↓ 34% |
可视化结果
三种地貌DEM数据
特征点选取示意图

水文流域分析
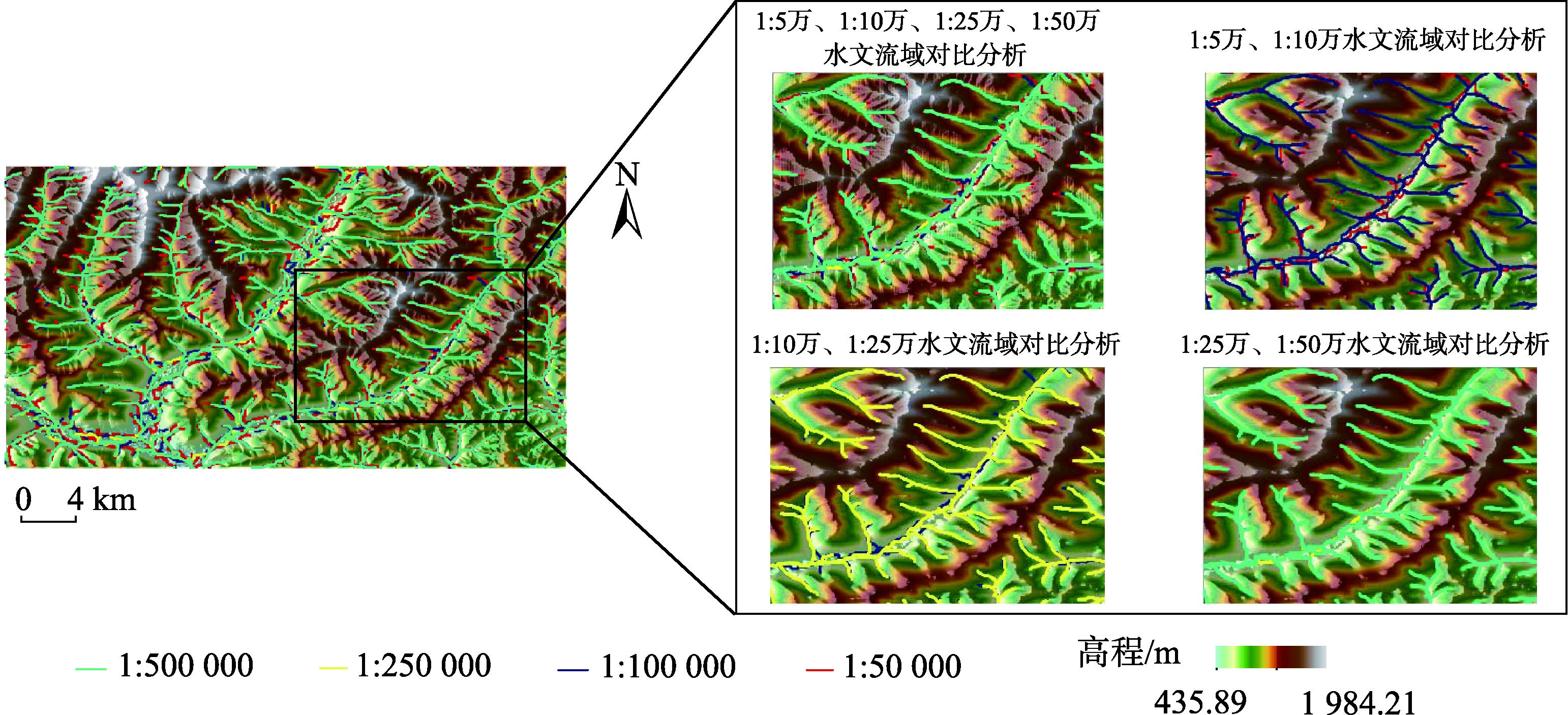
方法优势
特征保持
有效保留地貌骨架特征和地形细节
适用性强
适用于山地、丘陵、平原等多种地貌类型
精度提升
MAE和RMSE显著降低,综合精度更高
自动化程度高
通过数学模型自动确定参数,减少人工干预
研究结论
主要成果
- 提出了基于曲率小波变换的DEM综合新方法
- 通过平面曲率计算突出局部地形几何特征
- 引入方根模型制定特征点选取规则
- 验证了方法在多种地貌类型中的有效性
创新点
- 将平面曲率与小波变换有机结合
- 建立尺度变化与分解层数的数学关系
- 构建特征点数量的动态调整机制
- 实现多尺度地形分析的精度提升
未来展望
算法优化
根据不同地形信息特点,自动且快速地确定小波分解函数,进一步提升算法的自适应能力
格式扩展
针对DEM数据的多种格式(矢量、TIN)特性,选择合适的参数以实现更广泛的应用